计及风力发电并网的配电网潮流优化
程站立,胡 枚,陈世雯
(安徽省电力公司马鞍山供电公司,安徽 马鞍山 243000)
0 引言
随着全球资源环境压力的不断增大,社会对环境保护、节能减排和可持续性发展的要求日益提高。同时,电力市场化进程的不断推进以及用户对电能可靠性和质量要求的不断提升,要求未来的电网必须能够提供更加安全、可靠、清洁、优质的电力供应,而具有灵活、清洁、安全、经济、友好等性能的支持各种分布式电源(微型燃气轮机、燃料电池、太阳能光伏发电、风力发电等)以“即插即用”的方式友好接入的智能电网就成了未来电网的发展方向[1]。
分布式电源(distributed generation,DG)是指在配电系统靠近用户侧引入的功率为数千瓦至50 MW的小型模块式、与环境兼容的独立电源。分布式发电具有投资少、占地小、建设周期短、节能、环保等特点。风电是具有可再生性的分布式电源,近年来随着中国能源结构的调整,风电日益得到重视,并制订了有关政策支持风电的快速发展,风电已成为分布式发电中发展最快的、最具有发展前景的一种发电方式[2]。
风电并入配电网对配电系统的网损和电压分布有重要的影响,而潮流计算是对其进行量化分析的主要手段。文献[3]在建立PQ模型时根据有功功率调整无功功率,在有功功率已知的情况下,根据有功功率与无功功率的近似解析式求得风场无功功率,然后进行计算。文献[4]在分析风电机的潮流模型的基础上,提出了RX模型,此模型充分考虑到了风力发电机的输出功率特性,在常规潮流迭代基础上增加了异步发电机的滑差迭代计算。但是该方法潮流方程维数较大,计算程序复杂。文献[5]利用蒙特卡罗方法仿真模拟风机风速,建立了包含风力发电机组的配电网无功优化模型,并采用静止无功补偿设备对配电网进行无功补偿。在分析风电机组潮流计算中常用的几种数学模型的基础上,采用了前推回带法计算了计及风力发电的配电网潮流,在潮流计算中考虑使用并联电容器对电网进行无功补偿,并建立了以全网的有功网损最小为目标函数的无功优化模型,并通过算例分析对所提的方法进行了仿真验证。
1 风力发电机组模型分析
1.1 风电机组的PQ等值模型
风电机组主要由风力机和异步发电机等主要元件组成[4]。在稳态情况下,风力机从风能中吸收的机械功率与风速的三次方成正比即

式中,r为空气密度,kg/m3;V为风速,m/s;A为风力机的扫掠面积,m2;Cp为风力机的风能利用系数,表明风轮机从风中获得的有用风能的比例,它是叶尖速比λ的函数,且有λ=ωr/v;r为风轮半径;ω为风轮角速度。
在电力系统潮流计算中的风电机组传统的处理方法是将其等值为PQ节点,并认为风电机组中电容器自动分组投切,以保持风电场的功率因数保持不变,即有

式中,θ是并网风电场的功率因数角。由于采用的是异步发电机,所以θ一般位于第四象限,tanθ为负。
1.2 风电机组的RX等值模型
在含风电机组的潮流计算中,RX等值模型基本思想是基于两个迭代过程,一是通过常规潮流迭代过程计算异步发电机的机端电压;二是通过异步发电机滑差的迭代过程计算异步发电机的滑差。根据能量守恒定律,风力机吸收的机械功率和异步发电机发出的电气功率理论上应该相等。因此,当异步风力发电机的电气功率与风力机吸收的机械功率的差值达到允许的误差范围时,说明风力发电机组达到稳定运行点。这种等值模型要基于以下两个假设[6]。
(1)在滑差s已知的情况下,电机在稳态情况下可以模拟等效成一个阻抗。
(2)风速和功率因数曲线在已知的情况下可以求出滑差的数值大小。
由异步发电机组等值电路原理图1可知,在RX等值模型中,其等值阻抗为
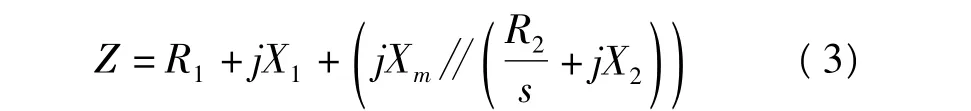

图1 异步发电机等值电路[4]
图1中,X1为定子漏抗;X2是转子漏抗;Xm是异步发电机的激磁电抗;R1是定子电阻;R2是转子电阻;Rm是励磁电阻;s为转差。
异步发电机组发出的有功功率P与转子电流I2,异步发电机的滑差s之间的关系为

采用RX等值模型方法能够较好地反映异步电机的特性,但由于需要两个迭代过程,其总的迭代次数多,计算负担重,同时收敛性变差。
1.3 风电机组的稳态等值模型及简化模型
目前,风力发电的机组一般都是异步发电机组。异步发电机在超同步运行的情况下以发电方式运行。它吸收风力机提供的机械能,发出有功功率。但是异步发电机本身无励磁装置,需要从电网或者电容器中吸收无功功率提供其建立磁场所需的励磁电流。多台风力机组按照一定规则排列构成风电场,风电场的功率为所有风电机组输出功率之和[7]。
由图1中的电路关系可知发电机的有功功率的表达式为

在不考虑并联电容器的情况下,发电机从电网中吸收的无功功率Q为


图2 异步发电机简化模型
在图1中,Xm>>X1且定子电阻和铁心的功率损耗与有功功率相比可忽略,因此,可以将励磁支路移至电路首端,得到简化的异步发电机Γ型等值电路,如图2所示。
若假设风电场的有功功率为风机的机械功率,可由电路连接关系得出风电机组无功功率的表达式。经过简化则式(6)可变为式(7),如下。

为了减少网络损耗,通常与风力发电机组并联安装电容器组。电容器组自动分组投切,以保证风力发电机组的功率因数在允许的范围内变动。带并联电容器组的风力发电机组的功率因数为[8]

式中,P为风力发电机输出的有功功率;Q为风力发电机吸收的无功功率;Qc为并联电容器输出的无功补偿容量,可以表示为

式中,cosφ1为发电机的初始功率因数;cosφ2为并联电容器组后的发电机功率因数。
并联电容器组的实际投入组数为

式中,[n]表示对分数取整数运算;QN为并联电容器的单位容量。考虑并联电容器组输出无功与电压幅值有关,风机从电网吸收的实际无功为

在潮流计算中根据每次得到的电压幅值由式(7)计算其吸收的无功,再根据要求达到的功率因数由式(9)和式(10)求出并联电容器的组数,最后由式(11)得到实际吸收的无功,这样就可以在下次潮流计算时把风机并网节点作为PQ节点进行潮流计算[3]。
2 改进的粒子群算法
由于基本粒子群算法过多的依赖于个体最优解和种群最优解的信息,搜索区域可能因此会受到限制,而且设置参数、种群的大小以及它们之间的关系也没有可供参考的准则,因此算法有开始效果好,接近最优解时收敛很慢等缺点。针对不同的优化问题,在基本粒子群优化算法基础上的许多改进己经提出并产生出一些新的粒子群优化算法模型[9]。
为保证算法的收敛性,ClERC提出了对PSO进行改进的收缩因子方法 (constriction factor method,CFM)。由于该方法定义了一个收缩因子K,所以该改进的PSO算法被称为PSO-cf,其定义如下。

式中,K是收缩因子;ω是惯性权值;c1和c2分别是加速常数;(t)是第i个粒子的位置;(t)是第i
这里将系统有功功率损耗和节点电压偏差最小作为目标函数,并采用罚因子的方式将多目标的无功优化模型转变成单目标的优化问题。具体目标函数如下。

式(15)中,Ri是支路电阻;Pi和Qi分别是支路的有功功率和无功功率;Ui是节点i上的电压幅值;Urat是节点参考电压(标幺值)取值为1.0 p.u.;λ是罚因子,这里取值为10。式(16)中,Sc1是补偿电容器的投切组数。
3 基于改进粒子群算法的配电网潮流优化步骤
前推回带法具有编程简单、计算效率高、且随着网络复杂程度的增加速度降低不大、收敛特性好等优点,特别适用于计算辐射型电网结构的潮流,是一种性能优异的配电网潮流算法[10]。因此这里拟采用此方法进行系统潮流计算。
进行潮流计算前,需要给定的初始量有风电场节点电压幅值、风力发电机的风速、定子和转子电抗、励磁电抗、并联电容器组的额定电压、并联电容器组额定电压下的单位容量以及进行无功补偿的并联电容器的投切百分比。具体的潮流计算过程如下。
①确定风机输出的有功功率,输入系统数据并初始化粒子种群;②由式(7)~式(11)计算风电场电容器组的安装组数以及初始时刻风力发电机吸收的无功功率和并联电容器组发出的无功功率;③调用前推回推潮流计算程序计算目标函数值,即分别计算群体中的每个粒子的潮流,得到每组控制变量下的有功损耗;④记录粒子当前的个体极值pbesti及目标函数值f(pbesti),从pbesti中确定整体极值gbest并记录gbest对应的目标函数值;⑤更新粒子飞行速度以及在解空间中的位置;⑥再次调用前推回推法计算系统潮流,重新判断各个粒子的目标函数值,如果f(pbesti+1)< f(pbesti)则更新pbesti,否则不更新;将每个粒子的适应值与整个粒子群的gbest相比较,如果较好则重新设置gbest,否则gbest值不变,重新初始化粒子群;⑦当满足全局最好位置连续若干次无变化或达到预先给定的最大迭代次数条件后,迭代停止,否则转入步骤(3);⑧输出补偿电容器的投切组数以及对应的网损值,潮流优化结束。
4 算例分析
采用图3所示的33母线配电系统进行分析。根据文献[10],系统电压基准值为12.66 kV,视在功率基准值为10000 kV·A,系统总的有功负荷是3715.0 kW,总无功负荷是2300.0 kW。在节点17、24、32并入3台风机,单台风力发电机的额定容量为600 kW,其额定电压为0.69 kV,功率因数为0.89。在节点9、16、30并联3组补偿电容器,并联电容器组的额定电压为0.69 kV,每台并联电容器的额定容量为40 kvar,采用百分比值确定容量,调节精度为0.01。风电场的功率因数由初始的0.89提高到0.99。并联风机的参数参考文献[11]。潮流计算方法采用前推回带法。

图3 33母线测试系统
由于33母线系统是三相平衡系统,因此在潮流计算过程中只算其一相即可。风机并入前的33母线系统的节点电压幅值如图4所示。

图4 33母线系统节点电压幅值
由图4可以看出33母线系统的电压幅值在0.91~1.0 p.u.之间。潮流计算经过5次迭代后收敛,系统总的有功网损为405 kW。
在节点24、32、17并入风电机组后,潮流计算经过5次迭代收敛,迭代结束后的节点电压幅值与风机并网前比较如图5所示。

图5 含风电机组的系统电压幅值
由图5可以看出风机并网后向系统发出有功功率,供给与风电场节点相近的节点负荷,有效地提高了整个配电网的电压幅值水平,节点电压幅值范围为0.932~1.0 p.u.之间。潮流计算结束后得到系统有功网损为229 kW。
在节点9、16、30接入并联电容补偿器组后,应用改进的粒子群算法对配电网进行无功优化,试验次数为20次,种群规模为39,维数为3,收缩因子为0.7298,加速因子均为2.01,迭代收敛精度为10-6,控制变量范围为0~5。经过优化后的电压幅值与优化前相比较如图6所示。
采用改进粒子群算法的配电网潮流优化程序经过5次迭代后收敛,节点电压幅值为0.935~1.0 p.u.,优化补偿后的系统有功网损为195 kW,优化后的电容器的无功补偿容量分别为 23 kvar、30 kvar、40 kvar。相比没有优化的含风机的配电网,电压幅值有了进一步的提高,系统总的有功网损也有了显著的降低。采用改进的粒子群算法对含风机的配电网进行潮流优化不但没有增加潮流收敛需要的迭代次数,而且有效地降低了系统的有功网损,提高了节点电压幅值。证明所使用的潮流优化方法是正确的。

图6 优化后的系统电压幅值
5 结论
研究了计及风机并网的配电网潮流优化方法,通过比较分析风电场并网潮流计算的几种常用模型,选用带补偿电容的风机稳态等值模型作为研究对象,并采用改进的粒子群算法对风机并网的配电网潮流进行了优化。仿真实验结果表明,该算法可行,对于减少网络的功率损耗和提高节点电压幅值有显著的作用,为各种DG的并网优化运行提供了理论和方法参考。
[1]陈述勇,宋书芬,李兰欣,等.智能电网技术综述[J].电网技术,2009,33(8):1-7.
[2]雷亚洲.与风电并网相关的研究课题[J].电力系统自动化,2003,27(8):84-89.
[3]李新,彭怡,赵晶晶,等.分布式电源并网的潮流计算[J].电力系统保护与控制,2009,37(17):78-81,87.
[4]徐娇,李兴源.异步发电机组的简化RX模型及潮流计算[J].电力系统自动化,2008,32(1):22-25.
[5]陈琳,钟金,倪以信,等.含分布式发电的配电网无功优化[J].中国电机工程学报,2006,30(14):20-24.
[6]刘洋,康凯,王邦惠,等.含风电系统的潮流计算分析[J].山东电力技术,2009(4):21-24.
[7]胡敏,周任军,杨洪明,等.考虑风力发电的系统无功优化模型和算法[J].长沙理工大学学报:自然科学版,2009,6(1):43-48.
[8]王守相,江兴月,王成山.含风力发电机组的配电网潮流计算[J].电网技术,2006,30(21):42-45,61.
[9]刘述奎.基于自适应聚焦粒子群算法的电力系统无功优化[D].成都:西南交通大学,2009.
[10]王守相,王成山.现代配电系统分析[M].北京:高等教育出版社,2007.
[11]顾威,李兴源,魏巍.异步发电机稳态模型研究[J].四川电力技术,2009,32(3):20-24.

