负荷频率特性对孤网频率稳定性影响分析
周 专,姚秀萍,,常喜强,申盛召
(1.新疆大学电气工程学院,新疆 乌鲁木齐 830047;2.新疆电力调度通信中心,新疆 乌鲁木齐 830002)
0 引言
随着中国经济的发展,中国的电网规模在不断扩大,区间联网送电规模也在不断增大,这有利于对各地区自然资源合理利用,大力发展清洁能源。但区间联络线由于输电走廊限制等原因相对较弱,一旦发生解列事故,容易形成送端(受端)孤立电网,将导致局部系统功率严重失衡,送端电网功率大量剩余,而受端电网功率严重缺额,系统的频率稳定问题就会凸显出来[1-3]。
各地区由于经济发展的侧重点不同,造成有的地区以工业负荷为主,有的地区以农业负荷为主。由于负荷的频率特性不同,造成不同负荷模型对系统频率调节效应不同。因此在电力系统仿真时对各地区负荷模型的正确选取是保证仿真结果正确反映实际电网运行的重要措施。目前中国对负荷特性的研究有很多,文献[4]主要是研究负荷特性对电压稳定性影响;文献[5]讨论了负荷频率特性对低频减载的影响;文献[6]研究负荷动态特性对系统静态电压稳定性影响。还没有文献从孤网的角度考虑负荷频率特性对孤网频率稳定性的影响,因此下面以新疆和田地区电网为研究对象,分析负荷频率特性对孤网频率稳定性的影响,通过改变孤网中负荷模型,以及各种负荷在孤网中的比例,得出不同的负荷模型对孤网频率稳定性影响程度不同结论,运用PSASP仿真验证了相关结论。对实际电网稳定计算时负荷模型的选取具有重要的参考价值。
1 电力系统频率调整特性
电力系统功率频率特性是指系统有功功率不平衡时频率的变化特性,它是负荷频率特性、发电机频率特性以及电压影响的综合结果。
电网中有功功率和频率相互影响,当系统中有功功率不平衡量为ΔP时,系统中的频率变化量Δf可表示为

若系统中的发电机和负荷同时参与系统频率调节,则系统的单位调节功率(Ks)可表示为
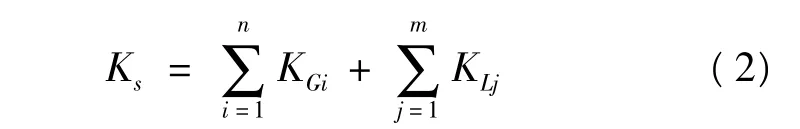
式中,KGi为某台发电机的单位调节功率;KLj为某系统中负荷类型的单位调节功率。
在电网负荷发生变化时,依靠发电机的调速器以及负荷调节效应的共同作用而使电网在新的频率下稳定运行[7]。电网频率调节过程如图1所示。
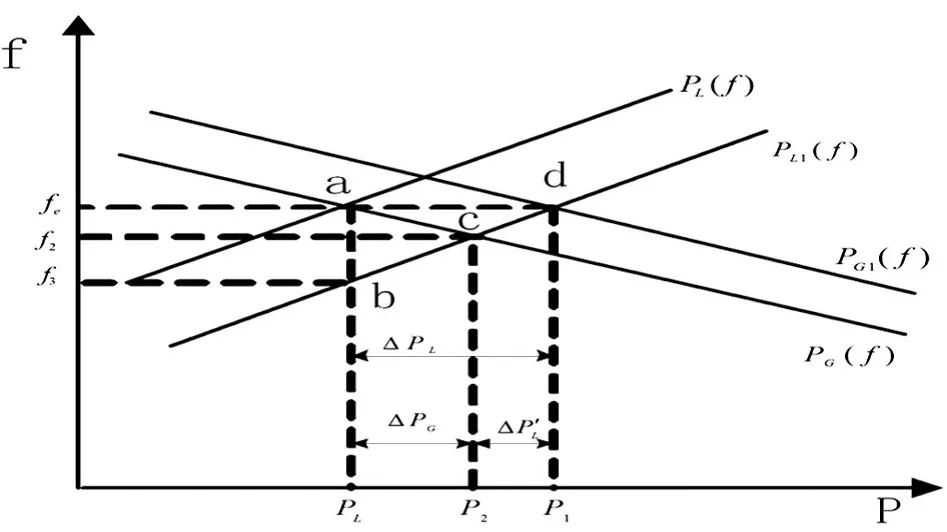
图1 电网频率调节示意图
如图1所示,电网正常稳定运行在a点,此时电网功率平衡。当电网中负荷从PL变为PL1时系统将出现功率缺额,导致发电机转速下降,从而使系统中的频率下降。若系统中常规机组调速系统没有投运,系统中发电机组出力保持不变,系统中只能通过负荷调节效应稳定在b点,系统中的频率将大幅下降。在有调速器的情况下,调速器和负荷调节效应同时参与消除出现的功率缺额。调速器动作增大发电机组出力,频率降低使得负荷有功功率PL减小,最终稳定在c点,系统频率稳定在合理的范围内。
2 负荷频率特性分析
当系统频率发生变化时,系统中的有功功率负荷也会发生变化,这种特性称之为负荷的频率特性[8]。不考虑电压波动的影响,系统频率和负荷的有功功率的关系满足下式。

式(1)的一般表达式为
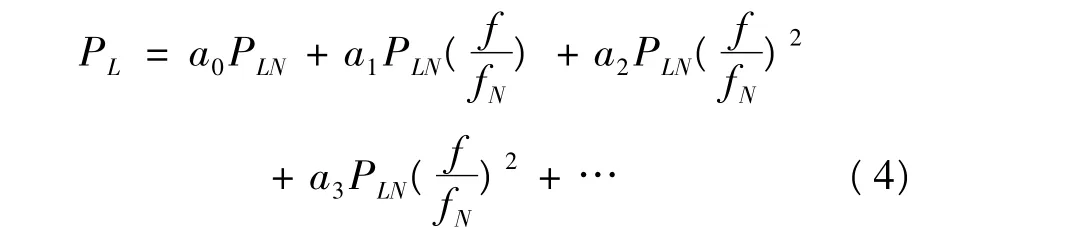
式(2)中,PL为频率等于f时整个系统的有功负荷;PLN为频率等于fN时整个系统的有功负荷;ai(i=0,1,2,…)为与系统额定频率的i次方成正比的负荷在PLN中所占的百分比。
式(2)的标幺值表达式为

由于系统中与频率的三次方以上成正比的负荷很少,可以忽略其影响,再将上式对频率微分,得
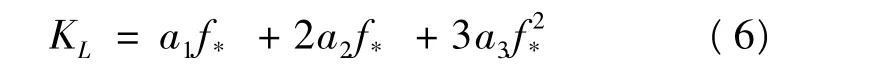
式中,KL为负荷的频率调节效应系数。不同的负荷支路因其组成不同,其KL值也不相同。
当系统的频率变化时,具有不同的频率调节效应的负荷变化也是不同的,假设有两种不同频率调节效应的负荷,它们的有功功率和频率的关系式分别为

如图2所示,当频率从f2(f2=50 Hz)下降到f1时,负荷1和负荷2吸收的有功功率变化量不同。

图2 负荷的频率特性曲线
图2中ΔP1>ΔP2,说明负荷1比负荷2对频率的变化更敏感,即KL1>KL2。由此可以得出:当系统频率降低时,频率调节系数大的负荷从系统吸收的有功功率减少得更快。因此在孤网中,优先考虑频率调节系数大的负荷,这样在频率下降的时候,可以通过负荷自身的频率调节效应,减少从系统吸收的功率,有利于孤网稳定保持网内功率平衡。
3 负荷频率特性对孤网频率稳定性影响分析
当发生有功功率缺额时,电力系统频率下降程度和下降速度主要取决于4个因素[9-10]:发电功率缺额数量、剩余发电机总转动惯量M、负荷的频率调节效应系数KL、系统旋转备用容量。其中功率缺额、发电机转动惯量及系统旋转备用为已知量,而负荷频率特性为系统固有特性。当系统频率变化时,系统的负荷功率也会随频率变化。
考虑到系统阻尼作用,出现有功缺额后频率可以表示成[11]

式中,f0为系统初始频率;Pa为系统功率不平衡量;D为系统总阻尼系数;M为系统惯性常数。M一般取4~8,系统总阻尼系数D一般在2以上,当时间较长时(t>40 s),考虑极端情况M取最大值8,D取最小值2≈0.00067(可以忽略)。
因此孤网最终稳态频率只取决于孤网功率不平衡量Pa及孤网总阻尼系数D,而与惯性常数M无关。惯性常数M只与孤网初始频率变化过程及孤网最低频率对应时间存在一定影响,但随着时间增大其对孤网稳态频率影响逐渐减少。
在不考虑系统旋转备用的情况下,可近似认为孤网总阻尼系数D=KL,由式(9)可知,虽然KL的大小不影响孤网频率的初始下降率,但负荷频率特性却对系统最低频率及稳态频率有重要的影响。KL值大的负荷在频率下降过程中从孤网中吸收的有功负荷减少得更快,因此孤网最低频率及稳态频率较高,有利于孤网功率平衡和频率快速恢复。
4 仿真分析
和田电网目前通过单回286.3 km的220 kV玉莎线和单回167.87 km的110 kV叶皮线(正常方式下断开备用)与主网相连,距离主系统2000 km以上,与主系统联系极其薄弱。和田电网地理接线示意图如图3所示。
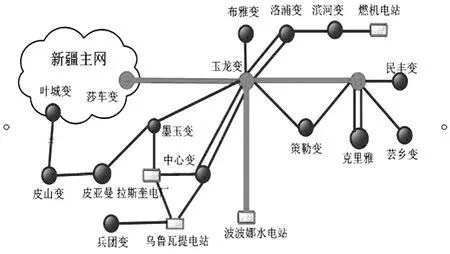
图3 和田电网地理接线示意图
和田地区负荷为240 MW,主要由波波娜水电站(3×50 MW)、乌鲁瓦提水电站(4×15 MW)向其提供电源。和田地区电网靠玉莎线与主网相连,来保持地区电网功率平衡。当玉莎线故障跳闸后,和田电网将与主网解裂孤网运行。此时和田电网功率不平衡出现功率缺额,孤网频率将降低,系统中的调速系统、低频低压减载装置动作。地区负荷频率特性影响低频减载装置动作情况,并且负荷的频率调节效应系数对系统频率稳定性有影响,因此负荷频率特性对孤网频率稳定性有很大的影响。下面对和田电网在不同负荷频率特性情况下进行仿真分析。
假定玉莎线发生永久性断线时玉莎线上传输功率为70 MW。和田电网中只有波波娜水电机组调速系统参与频率调节。
4.1 恒阻抗和感应电动机负荷
在运用PSASP程序对和田电网进行仿真时,假定和田地区负荷主要是恒阻抗和感应电动机组成。恒阻抗负荷与频率的变化无关,对孤网频率稳定性影响不太。感应电动机负荷与频率的一次方成正比,电网中感应电动机负荷比例(a1)的多少对电网频率稳定性影响很大。当地区负荷主要由这两种负荷组成时,该地区的频率稳定性主要受感应电动机的影响。图4为不同负荷比例情况下对应孤网运行的频率。
从图4可以看出,感应电动机负荷在孤网中所占比例不同时,孤网中频率变化不相同。随着感应电动机负荷所占比例增大,孤网的最低频率升高,同时孤网稳态频率也升高,孤网频率快速得到稳定。感应电动机负荷所占比例不同时对应的孤网频率特征如表1所示。
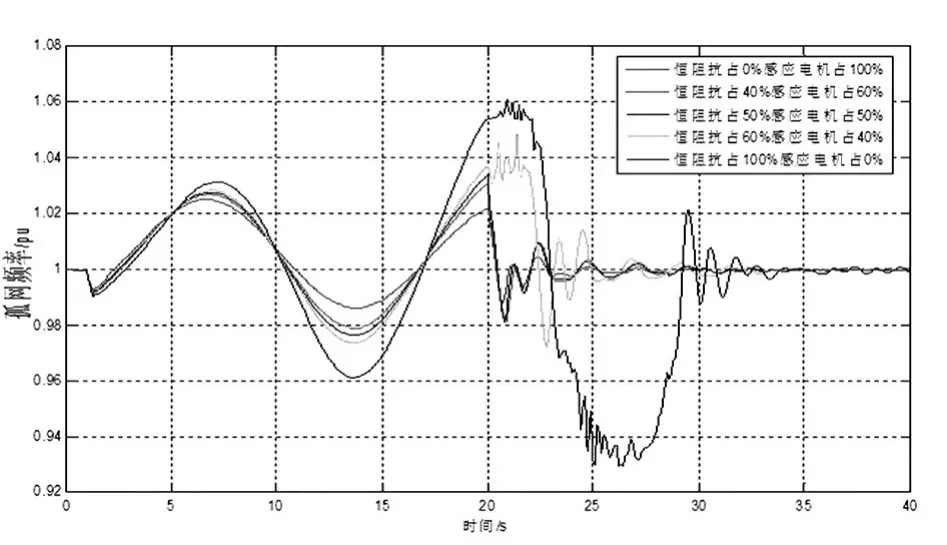
图4 不同负荷比例对应的孤网频率
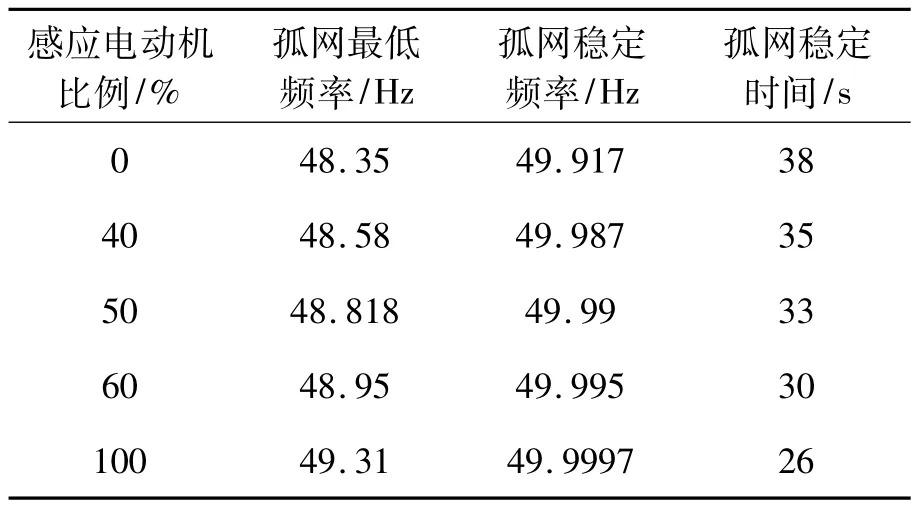
表1 感应电动机比例变化时对应的孤网频率特征
由式(6)可知,负荷的频率调节效应系数(KL)与感应电动机负荷所占比例(a1)有关。当系统中的感应电动机负荷增大时,对应系统中的负荷频率调节效应系数也随之增大。由表1可得,KL越大,孤网最低频率及稳态频率较高,孤网频率能快速恢复,有利于孤网功率平衡。
4.2 综合负荷
为了研究不同负荷模型对孤网频率稳定性的影响,在运用PSASP程序对和田电网进行仿真时,假定和田地区负荷采用PSASP程序中的综合负荷模型5,改变负荷模型中恒阻抗的比例。图5为不同恒阻抗比例情况下对应孤网运行的频率。

图5 负荷中恒阻抗比例变化对应的孤网频率
从图5可以看出,综合负荷模型在孤网中所占比例不同时,孤网中频率变化不相同,同时孤网频率出现波动。随着恒阻抗负荷所占比例增大,孤网的最低频率降低,同时孤网频率波动增大,直至不稳定。若电网中负荷是由恒阻抗和综合负荷组成,电网中的恒阻抗负荷比例直接影响系统的频率稳定性。因此在由恒阻抗和综合负荷模型组成的电网负荷对孤网频率稳定影响很大(见图6)。对比图4和图5可以得出,感应电动机负荷比综合负荷更有利于孤网的频率稳定性。因此在对电网进行仿真分析时要正确的选取负荷模型,不同的应用选取不同的负荷模型,这样才能准确地反应实际电网问题,将结果应用于实际电网分析。
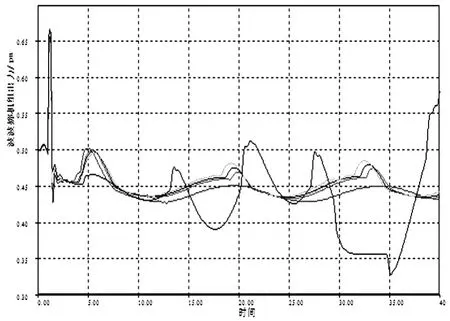
图6 负荷中恒阻抗比例变化对应的波波娜出力
5 结论
通过对孤网中不同负荷模型及负荷比例对孤网频率影响分析,得出以下结论。
(1)负荷的频率调节效应系数大的负荷在频率下降过程中从孤网中吸收的有功负荷减少得更快,孤网最低频率及稳态频率较高,有利于孤网功率平衡和频率快速恢复。
(2)负荷的频率调节效应系数(KL)与感应电动机负荷所占比例(a1)有关,系统中感应电动机的比例越大,对应的KL也越大,越有利于孤网频率稳定性。
(3)感应电动机负荷比综合负荷更有利于孤网的频率稳定性。
(4)在对电网进行仿真分析时要正确地选取负荷模型,不同的应用选取不同的负荷模型,这样才能准确地反应实际电网问题,将结果应用于实际电网分析。
[1]黄宗君,李兴源,晁剑,等.贵阳南部电网“7.7”事故的仿真反演和分析[J].电力系统自动化,2007,31(9):95-100.
[2]P.Kundur,周孝信,李兴源,译.电力系统稳定和控制[M].北京:中国电力出版社,2002.
[3]Horne J,Flynn D,Littler T.Frequency Stability Issues for Islanded Power Systems[C].IEEE PES Power System Conference and Exposition,2004.
[4]耿天翔.负荷特性对电压稳定性影响分析[J].科技创新导报,2012(10):83.
[5]熊小伏,周永忠,周家启.计及负荷频率特性的低频减载方案研究[J].中国电机工程学报,2005(19):48-51.
[6]段俊东,黄家兴.负荷动态特性变化对电力系统静态电压稳定性的影响研究[J].工矿自动化,2012(2):44-48.
[7]翟庆志,李艳军,刘明丹.电机学[M].北京:中国电力出版社,2002.
[8]刘健,毕鹏翔,董海鹏.复杂配电网简化分析与优化[M].北京:中国电力出版社,2002.
[9]汤涌,侯俊贤,刘文焯.电力系统数字仿真负荷模型中配电网络及无功补偿与感应电动机的模拟[J].中国电机工程学报,2005,25(3):8-12.
[10]赵强,王丽敏,刘肇旭.全国电网互联系统频率特性及低频减载方案[J].电网技术,2009,33(8):35-40.
[11]New W C,Brown B J,Goff P G,et al.Load Shedding,Load Restoration,and Generator Protection Using Solid-State Andelectromechanical Under Frequencyrelay[EB/OL].Generalelectric Company.http://pm.geindustrial.com/FAQ/Documents/489/GET-6449.pdf,1974.

