基于混合法的复杂配电系统的可靠性评估
陈嵩峰,宋明玉
(乐山电业局,四川 乐山 614000)
0 引言
供电网是电力系统中联系电源与用户的一个重要环节,其供电可靠性水平与电力用户有着直接的关系。分析系统可靠性的方法有多种,总的说来这些方法可分为两大类:解析法和模拟法。模拟法通常指蒙特卡洛模拟法[1-3],模拟运行的实际问题,通过状态选择,用统计方法得到可靠性指标。解析法[4-5]适合于网络规模较小而网络结构较强的系统。此外,还有其他许多方法:如故障树分析、逻辑图法。
在总结已取得的成果和经验的基础上,结合供电网络的实际特点和现状,提出一种网络等值法与改进故障树分析法相结合的供电网络可靠性分析方法,并对供电系统可靠性统计与分析进行了研究,并通过实例计算,验证了该方法的正确性。
1 供电系统可靠性评估方法
1.1 网络等值法原理
实际的供电网主要由主馈线和分支馈线构成。对于这种复杂的供电网,可以利用向上等效或向下等效[6]的方法将复杂的供电网络等值为一个简单的放射形供电网,从而简化供电网网络结构和减少计算量。采用向上等效的方法,将分支馈线对上级馈线的影响用一个串在上级馈线中的等效节点元件来表示,等效元件对上级线路的影响可以由等效元件的故障率λe、等效元件的年故障停电时间Ue、等效元件的故障修复时间Re来等效。具体过程如图1所示。
在初始网络结构图中,馈线1及其所连接的元件为最末层,包括分支线、熔断器及馈线上的主干线,它们发生故障会影响到本层负荷点的可靠性指标以及上层负荷点的可靠性。这种影响与馈线2上串联一个元件类似,所以可以用一个等效元件E1来等值馈线1上所有元件故障的影响,即将方框内的所有元件等效为元件E1,如图1(b)所示。同理,逐层向上等效,馈线2上的所有元件等效为元件E2,馈线3上的所有元件等效为元件E1,从而得到一个简化了的馈线网络,如图1(c)所示。等效元件对上级线路的影响可以由等效元件的故障率λe、等效元件的年故障停电时间Ue、等效元件的故障修复时间Re来等效。

图1 复杂供电系统的可靠性等值示意图
1.2 网络等值法等效参数的计算[7]
对负荷支路节点,由于它通常由变压器、负荷支路线及熔断器(可有可无)组成,它的等效故障率的求取必定会受到各元件的影响,因此有必要作适当的分析处理。如果分支线路带有熔断器,设此熔断器可靠工作的概率为Pr,如果负荷支路发生故障,影响到上级线路停电的概率为1-Pr,则此负荷支路对应的等效元件的故障率为λ'j=(1-Pr)(λjl+λjt),该负荷支路对应的等效元件的平均停电持续时间为 rj'=Uj'/λj'。
在网络等值过程中,分支馈线上的每个元件出现故障时,如果分支馈线的首端设有断路器,设断路器的可靠断开率为Pd,则这条分支馈线上的每一个节点故障导致上一级馈线故障的概率为1-Pd,那么,该分支馈线对上级线路影响的等效故障率为该分支馈线上所有线路及其所连元件的故障率之和乘以1-Pd,由于断路器配套有隔离开关,分支线路上的任一元件故障,隔离开关断开,因此等效该级馈线的等效元件的故障修复时间为隔离开关的动作时间;如果分支馈线首端未设有断路器,则分支馈线上的任一元件故障都会导致上级线路停运,那么,该分支馈线对上级线路影响的等效故障率为该分支馈线上所有线路及其所连接元件的故障率之和,其故障停运时间根据分支馈线结构而定。
2 改进的FMEA
2.1 故障模式后果分析法原理
故障模式后果分析法(failure mode and effect analysis,FMEA)是供电网可靠性分析的基础方法,其基本思想是,首先假定系统的故障元件,然后对该元件故障引起的系统状态改变进行分析,进而找出受影响的线路及停电的负荷点。重复此过程直至枚举完所有的系统元件,按因果关系归纳成表。对影响同一负荷点的各元件故障率和修复时间,根据逻辑关系进行计算叠加,可得负荷点指标并进而求得系统的可靠性指标[8]。
数学描述:分析一次故障事件。馈线上可能有用户变压器、开关、线路三类元件故障,考虑一段上所有可能出现的故障事件,结合元件可靠性数据,得到一段上(假设为第k段)所有故障事件引起的用户停电持续时间(时户数)。
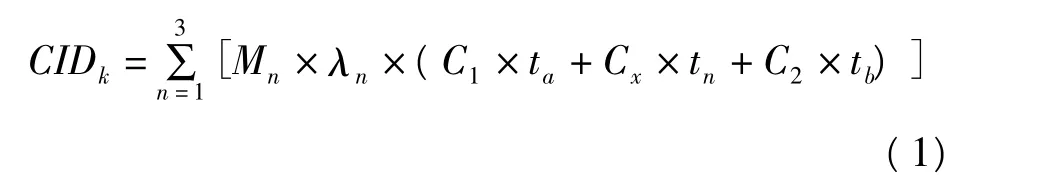
式中,Mn为段上第n类元件的台数(线路取平均分段长度,用户变压器取台数,开关一般为1个);λn为第n类元件的故障率;tn为第n类元件故障排除时间;ta为出线开关、分段开关操作时间;tb为联络开关操作时间;C1为故障段之前能由母线恢复供电的所有用户数之和;C2为故障段之后能由联络线恢复供电的所有用户数之和;Cx为故障期间不能恢复供电的所有用户数之和。
以此逐一计算馈线中各段的停电时户数,得到一整条馈线的停电时户数,进而得到变电站及整个供电网的停电时户数。
2.2 改进的故障模式后果分析法
由于故障模式后果分析法运算量大,运算时间长,不利于用在大型的供电网系统。部分学者以故障模式后果分析法为基本原理,对供电网拓扑进行分析,建立故障关联矩阵,根据故障关联矩阵的计算得出各个负荷点的可靠性指标,最后总和各负荷点可靠性指标,得出整个供电系统的可靠性。这个方法与FMEA法比较,由于只通过了矩阵运算,减少了运算量和预算时间,矩阵的加入使得计算过程更加简单明了,同时具有良好的扩展性和实用性。但是随着系统的扩大,矩阵的维数也会随着增加,计算量同时增加。因此,先通过网络等值,将复杂的供电网系统简化成简单的主馈线系统,然后再利用改进了的故障模式后果分析法计算。
3 计算实例
3.1 原始数据
算例结构参考IEEE RBTS母线6的主馈线4[6],该馈线包括 30 条线路、23 个负荷点、23 个熔断器,23个供电变压器、4个断路器及1个分段开关。设熔断器为100%的可靠熔断;线路的故障率取为0.05次/年·km,每段线路修复时间均取为4 h;断路器故障率取0.002次/年,修复时间取4 h;变压器故障率取为0.015次/年,修复时间取为200 h,切换到备用变压器的时间为1 h;分段开关的操作时间为20 min;联络开关的倒闸时间为1 h。
3.2 计算结果
在计算供电网可靠性指标时,认为发电系统、输电系统都是可靠的,发电系统总能满足负荷的要求。假设系统各元件都是独立的,串联元件可以合并成一个等效的元件。下面分几种情况来求各负荷点的可靠性指标。
1)供电变压器不设备用,断路器的可靠动作率为80%,设隔离开关;
2)供电变压器不设备用,断路器的可靠动作率为100%,设隔离开关;
3)供电变压器设备用,断路器的可靠动作率为80%,不设隔离开关;
4)供电变压器不设备用,断路器的可靠动作率为80%,不设隔离开关;
在以上4种情况下,计算分支线路向上等效的过程中,等效元件的故障率λ、年故障时间U以及故障修复时间r是相同的,因为熔断器是100%可靠工作的。
对该系统进行网络等值,得到的等效元件可靠性参数于表1。
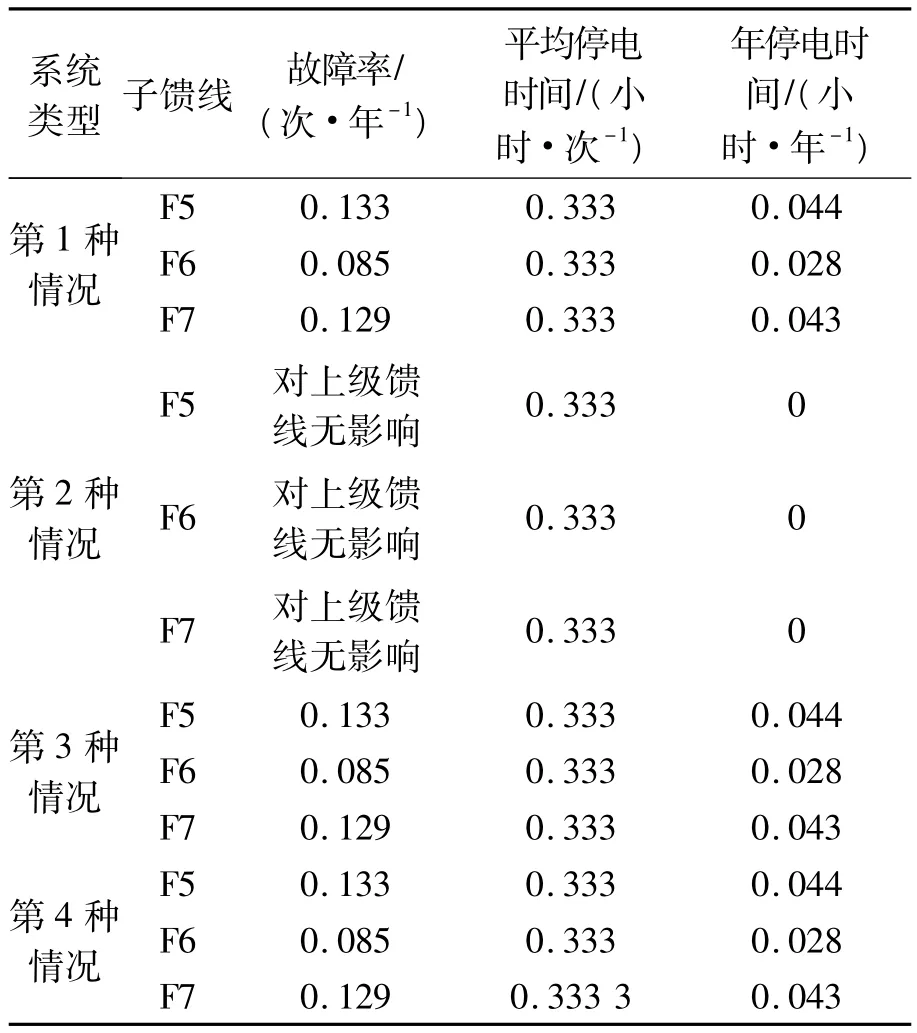
表1 分支馈线等效元件可靠性参数

表2 部分负荷点可靠性参数
4 可靠性分析
由求得的系统可靠性指标可以看出,第4种情况:供电变不设备用,断路器的可靠动作率为80%,不设隔离开关,这种情况下,系统可靠性最差,用户断电时间长;在第3种情况,增加了供电网变压器备用,缩小了由于变压器检修而产生的停电时间,用户停电持续时间大大降低;第1种情况在第四种的情况下增设了隔离开关,因此缩小了停电范围;第2种情况考虑了断路器的可靠操作率,可以看出,在断路器能够100%动作的情况下系统的可靠性更高。
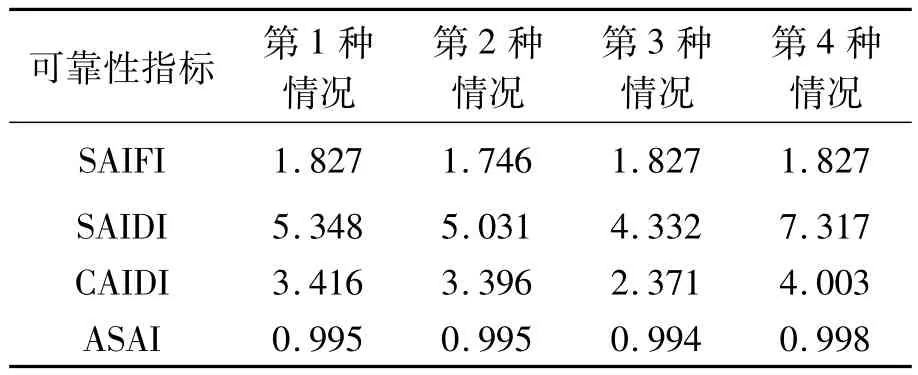
表3 系统可靠性指标
因此,可以看出,对于同一网络,不同的接线方式下,其系统可靠性指标有很大的不同。对可靠性较差的网络,可以采取一定的增强措施,如加装主馈线隔离开关、加分支线保护、备用供电变压器、增加备用电源等方式来增加其运行灵活性,从而提高其可靠性指标。
[1]徐纪法.供电可靠性综述[J].大众用电,2003(9):36-37.
[2]L G.Monte Carlo Simulation Based Reliability Studies of a Distribution Test system[J].Electric Power Systems Research,2000,54(1):55-65.
[3]别朝红,王锡凡.蒙特卡洛法在评估电力系统可靠性的应用[J].电力系统自动化,1997,21(6):68-75.
[4]霍利民,朱永利,张在玲,等.贝叶斯网络在供电系统可靠性评估中的应用[J].电工技术学报,2004,19(8):113-118.
[5]卢锦玲,栗然,刘艳,等.基于状态空间法的地区环式供电网可靠性分析[J].电力系统自动化,2003(11):21-27.
[6]万国成,任震,田翔.供电网可靠性评估的网络等值法模型研究[J].中国电机工程学报,2003,23(5):48-52.
[7]周云海,曹小伟,危雪.基于网络等值法的配电网可靠性研究[J].电气开关,2008(2):20-24.
[8]汪穗峰.供电网可靠性定量分析研究综述[J].继电器2008,36(3):78-83.

