考虑环境约束的中国区域全要素生产率增长——基于Hicks－Moorsteen指数方法

杨向阳，周佳慧，童馨乐

（南京财经大学a．国际经贸学院；b．金融学院，江苏 南京 210046）

一、引 言

改革开放以来的中国经济发展举世瞩目，经济总量目前已跃居世界第二位，这与快速推进的工业化进程密不可分，但由此引发的资源和环境问题也已成为中国经济发展中的焦点之一。在此背景下，有关环境约束对中国经济绩效的影响逐渐成为学术界讨 论 的 重 要 主 题［1－3］，而 全 要 素 生 产 率 （Total Factor Productivity，TFP）作为决定一个国家和地区长期经济增长的关键因素，无疑是研究者考察的重点内容，这在许旭等人、王兵等人、王姗姗等人的研究中得到了充分体现［4－6］。通过梳理现有研究环境约束对中国全要素生产率影响的文献，笔者发现尽管在时期跨度和研究对象、内容、结果等方面存在一定分歧，但对研究方法的使用却相对集中，特别是以Malmquist指数为基础的分析方法，是相当部分研究者的选择。

测度全要素生产率的基本方法大致可分为两类，即以随机前沿分析为代表的参数方法与以数据包络分析为代表的非参数方法。在具体的方法选择和应用方面，这两类方法并无绝对的优劣之分，基本选择主要决定于基本假设、分析对象和数据可得性［7］；就非参数方法而言，尽管Fare等人提出的Malmquist指数方法应用非常广泛［8］，但对技术规模报酬（这一性质的界定非常重要）的处理问题，学术界仍存在着分歧［9］；Grifell－Tatje等人指出非固定规模报酬的存在，导致Malmquist指数难以精确测度生产率变化，且这种偏差具有系统性，主要取决于测算中所使用的距离函数［10］；Wheelock等人认为，当不同时期一个厂商的位置不变时，规模效率变化将完全取决于可变规模报酬估计下的技术移动，而在固定规模报酬条件之下并不会发生技术变化，相应的估计技术在统计上并不一致［11］；Coelli等人则强调了对任何技术施加固定规模报酬的重要性，在计算Malmquist指数时，无论是微观数据还是总量数据，就估计距离函数而言都是适用的，如果没有固定规模报酬的假定，所得出的估计结果可能无法正确测度由规模经济引起的 TFP变化［12］。事实上，如果规模效率变化存在，实际生产技术必须是可变规模报酬技术，而Fare等人对技术变化测算反映的则是固定规模报酬前沿面［8］。理论上，衡量总产出和总投入比率的任何全要素生产率指数都应是一种理想化指数，这意味着不仅在数学形式上是完美的，而且在分解全要素生产率时也具有对应的经济含义。在最近的研究中，O’Donnell指出理想化全要素生产率指数包括：Fisher指数、Konus指数、Tornqvist指数和 Hicks－Moorsteen指数，但不包括 Malmquist指数［13］；尽管Caves等人首先倡导了Malmquist指数的应用［14］，但并没有构建理想化的TFP指数，除固定规模报酬等特定情形外，Malmquist指数在估计全要素生产率变化时是有偏差的，且所分解的技术变化和效率变化也有偏差［12］。为了避免非参数 Malmquist指数中的不足，O’Donnell提出了新的TFP分析方法，构造出具有乘积特征的理想化的Hicks－Moorsteen指数，即给定一个多投入与多产出情形，该方法既可度量TFP变化，也将其进一步分解为技术变化和不同种类的效率变化，且没有任何关于厂商行为最优化、市场结构或规模报酬等方面的限制性假设条件［13］。本质上，Hicks－Moorsteen指数是Malmquist产出量和投入量指数的比值［15－17］，目前在实证分析中的应用还很少。

综上所述，重新估算基于环境约束的中国区域全要素生产率，具有重要的学术价值和现实意义，这也是笔者研究的基本出发点。本文对已有文献的延伸和拓展主要体现在两个方面：一是研究方法的改进。与现有研究较多采用Malmquist指数方法估计全要素生产率的做法不同，本文采用理想化的Hicks－Moorsteen指数方法，重新估算和分解考虑环境约束后的全要素生产率增长情况；二是研究视角的聚焦。将区域因素放在更为突出的位置，同时采用三大区域和八大综合经济区两种区域划分方式，更为深入地考察中国全要素生产率增长的区域特征，为政府政策调整和优化提供依据。

二、研究方法

（一）Hicks－Moorsteen指数的构建

度量TFP的Hicks－Moorsteen指数为：

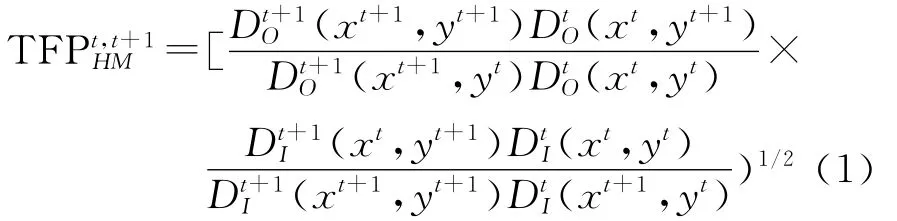
其中DO（x，y）和DI（x，y）分别表示产出距离函数和投入距离函数。根据Shephard可以得到：DTO（x，y）＝ min ｛δ＞0：（x，y／δ）∈P｝，DIT（x，y）＝max｛ρ＞0：（x／ρ，y）∈P｝，P表示时期T的生产可能性集合［18］。运用数据包络分析方法（Data Envelop A-nalysis，DEA），根据 O’Donnell的线性规划求解思路，可以计算出上述距离函数［19－20］。为了说明任一理想化的TFP指数都可分解为技术进步和不同种类的效率，假定在二维坐标系里，以多投入与多产出厂商为例说明（见图1）。

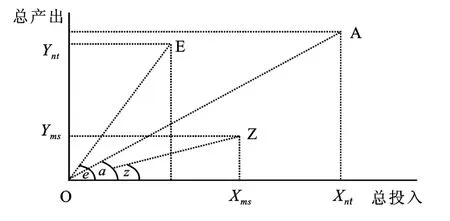
图1 理想化的全要素生产率指数分解图

根据图1，射线OA的斜率等于TFPnt，且厂商m在时期s的TFPms等于射线OZ的斜率，则TFPnt＝Ynt／Xnt＝tana和TFPms＝Yms／Xms＝tanz，而TFPms，nt＝tana／tanz是反映厂商n和厂商m在时期s和时期t的TFP指数。这样，任一具有乘积特征的理想化TFP指数均可表示为正切三角函数的比值。假设e表示任一射线OE（E点为非负）与横轴形成的角度，则厂商m和厂商n间的TFP变化可 分 解 为：TFPms，nt＝tana／tanz＝ （tana／tane）（tane／tanz）。按照这一思路，借助任一非负点形成的直线（如E点），可进一步分解具有乘积特征的理想化TFP指数。

（二）Hicks－Moorsteen指数的分解

在以上分析思路的基础上，O’Donnell将Hicks－Moorsteen指数分解为技术进步和不同种类的效率［10］，具体分解思路和过程，结合图2详细说明。

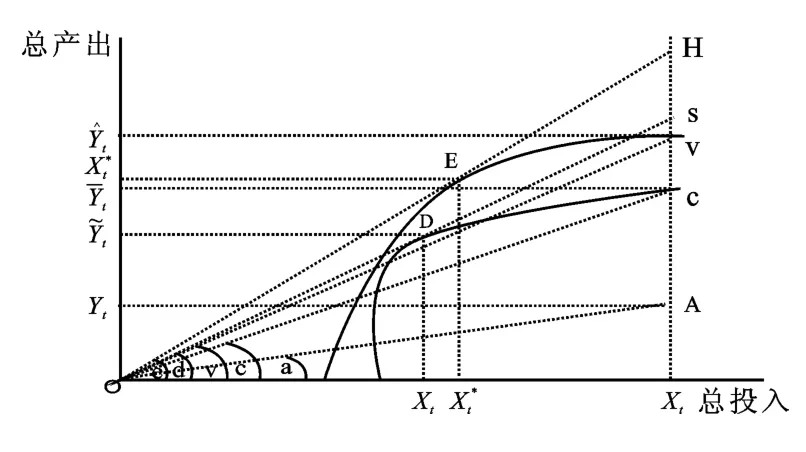
图2 基于产出的Hicks－Moorsteen全要素生产率指数分解图

产出技术效率（OTE）：图2中A、C和V点为投入产出组合，曲线DC表示其中一个受到生产可能性集合约束的边界。厂商将产出从A点扩大到C点，总产出和TFP水平提高，垂直距离AC为产出技术效率：OTEt＝Yt／＝tana／tanc表示现有技术约束下给定投入xt和产出yt时的最大总产出；相应地，厂商A的TFP和最大TFP可分别定义为Yt／Xt＝tana和／Xt＝tanc。

产出规模效率（OSE）：改善技术效率可提高TFP，厂商A在技术上有效的C点时TFP并非最大；若投入产出比例固定，厂商A移动到D点时（射线OS与曲线DC的切点，即组合不变最优规模点）TFP最大。垂直距离CS为产出规模效率：OSEt＝／Xt）／（Y／）＝tanc／tand，Y槇 和X槇 分别表示在组合不变最优规模点的总产出和总投入。

外加水分通常以游离水的形式存在，水分活度高，在后续的饲料加工如加热、挤压制粒、冷却、输送、储存中容易挥发损失，同时也容易引起饲料霉变。因此通过添加水分活度降低剂（保湿剂）来降低水分活度，有利于改善调质效果，减少水分在后续加工过程的损失，同时有利于提高生产效率，获得高质量的颗粒饲料，还有利于颗粒成品的储存。然而，有关水分活度降低剂在食品加工中应用研究较多，而在饲料加工中的应用国内研究报道甚少。国外有一定数量的在宠物饲料生产中应用的研究文献。

纯产出组合效率（OME）：如果放松厂商生产可能性边界受到限制的假设，厂商生产可能性边界可向外移动，取消产出组合限制后，厂商A可将总产出从C点提高到V点。纯产出组合效率OMEt＝／）＝／Xt）／／Xt）＝tanc／tanv，＾Y表示使用投入xt获得的最大总产出。

残余产出规模效率（ROSE）：改善技术效率和组合效率可提高TFP。在技术效率和组合效率均有效的V点，厂商TFP并非最大，图2中只有E点TFP最大。垂直距离VH表示残余产出规模效率：ROSEt＝ （＾Yt／Xt）／（Y＊t／X＊t）＝tanv／tane，Y＊t和X＊t分别为E点的总产出和总投入。

残余组合效率（RME）：记 TFP＊t＝Y＊t／X＊t＝tane为技术可变下投入组合中的最大TFP，垂直距离SH表示残余组合效率：RMEt＝（槇Yt／槇Xt）／（Y＊t／X＊t）＝tand／tane，衡量的是组合不变最优规模点的TFP与最大生产率点的TFP之间的差异。

TFP效率（TFPE）：综上所述，厂商从 A点移动到E点的TFP变化，表示基于产出的TFP效率：TFPEt＝TFPt／TFP＊t＝tana／tane＝（tana／tanc）×（tanc／tanv）×（tanv／tane）。与以上所讨论和定义的效率测度方法相对应，可以得到：

全要素生产率（TFP）：进一步分解TFP可得到TFPt＝TFP＊t×（OTEt×OMEt×ROSEt）和TFPt＝TFP＊t×（OTEt×OSEt×RMEt）。比较时期s厂商m与时期t厂商n的TFP指数值，则：

式（4）、（5）等式右边第一项表示技术进步变化，度量的是在技术可得情况下，时期t与时期s的最大TFP之间的差异。TFP＊t／TFP＊s大于1表示技术进步水平提高，衡量的是通过E点的射线斜率的变化。相比之下，Fare等人在分解 Malmquist TFP指数时，计算的是通过D点的射线斜率变化。因此，这里的技术进步包括组合效应，且不同厂商之间存在显著个体差异。相应地，等式右边第二项表示技术效率变化、（残余）组合效率变化和（残余）规模效率变化。

三、数据说明

本文的分析样本期为2000—2008年，以中国大陆地区31个行政省为基本分析单位，具体产出投入变量数据的选取和处理情况如下：

产出：“好”产出用各省的实际地区生产总值表示，并按1978年不变价格指数进行缩减；“坏”产出方面参照胡鞍钢等人的研究［21］，结合分析样本时期的选择及数据可得性，最终选取工业废水排放总量和工业SO2排放量作为替代。

资本投入：各省资本投入用资本存量来衡量。一般地，该数据可根据有关资本形成以及每年固定资产投资的数据推算而得，这里根据国际通用的永续盘存法进行估计。定义本期资本存量为上一期资本存量加上当年投资再减去折旧，即Kit＝Iit＋（1－δi）Kit－1，其中Kit是i省t年资本存量，Iit是i省t年投资额，δi是i省折旧率。关于基期资本存量，以1978年基期，采用Hall等人的折旧—贴现法来估算［22］，具体估算方法如下：K1978＝I1978／（g＋δ），其中投资用1978年固定资本形成总额来替代，g表示1978—2008年投资几何平均增长率，δ表示资本折旧率，这里取值为6%。在估计上面的各省资本存量之前，用分省固定资产投资价格指数折算实际资本形成总额，该指数国家统计局从1991年开始公布，可以满足分析的需要。

以上分析所需数据来源于《中国统计年鉴》（1999—2009）、《中国国内生产总值核算历史资料（1952—1995）》、《中国国内生产总值核算历史资料（1996—2002）》。结合分析目标，对中国区域差异的考察主要借助两种划分方式来展开：第一，按传统的东中西部地区划分方式，其中东部地区包括11个省份（北京、天津、河北、辽宁、上海、江苏、浙江、福建、山东、广东、海南），中部地区包括8个省份（山西、吉林、黑龙江、安徽、江西、河南、湖北、湖南）；西部地区包括12个省份（内蒙古、广西、重庆、四川、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆）；第二，按国务院发展研究中心提出的八大综合经济区划分方式，具体包括北部沿海综合经济区（北京、天津、河北、山东）、东部沿海综合经济区（上海、江苏、浙江）、南部沿海综合经济区（福建、广东、海南）、黄河中游综合经济区（陕西、山西、河南、内蒙古）、长江中游综合经济区（湖北、湖南、江西、安徽）、东北综合经济区（辽宁、吉林、黑龙江）、大西南综合经济区（云南、贵州、四川、重庆、广西）、大西北综合经济区（甘肃、青海、宁夏、西藏、新疆）。

四、实证结果分析

综合上述分析，根据式（4），在可变规模报酬条件下，使用中国省级面板数据，具体估算了基于产出的各省2000—2008年逐年的Hicks－Moorsteen全要素生产率指数，并做了进一步分解。在此基础上，将各省的估算结果进行汇总平均，由此得到全国总体、三大经济区域、八大综合经济区的全要素生产率增长情况①为简便之，表1直接报告了汇总以后基于产出的估计结果，而残余组合效率和残余规模效率在现有技术条件下无法估计，因此这里也没有报告这两个指标的结果。如有需要详细估计结果者，可与作者联系。。

（一）总体结果分析

表1是2000—2008年中国Hicks－Moorsteen全要素生产率指数及其分解结果。

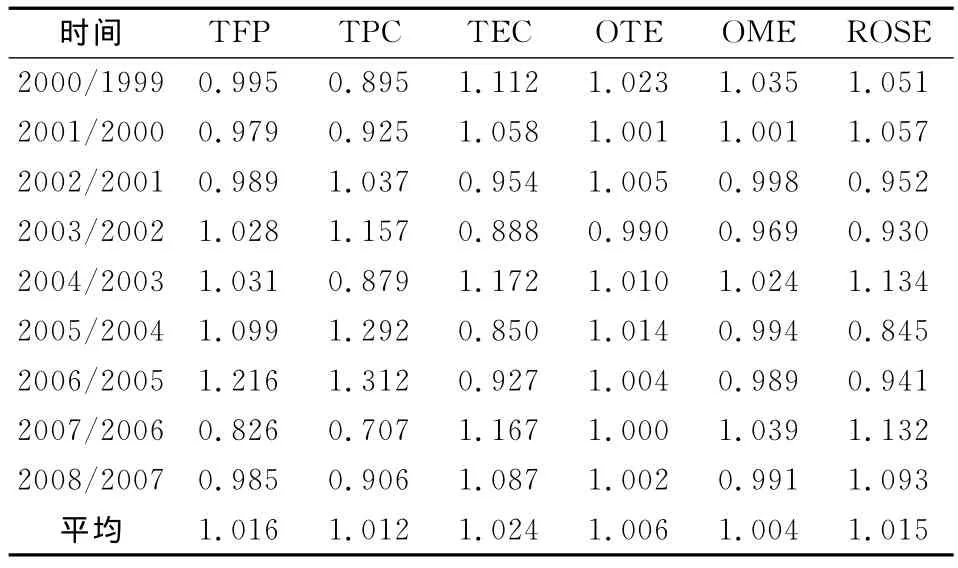
表1 中国Hicks－Moorsteen全要素生产率指数及其分解结果表

根据表1可看出：

第一，从总体看，在考虑了环境约束的影响后，2000—2008年中国全要素生产率的平均增长率为1．69%，这主要得益于技术效率的改善，平均增长率为2．43%；技术进步水平的提高，平均增长率为1．26%，但二者的增长率均具有明显的波动性，并呈现出明显的反向变化态势。

第二，从动态变化趋势看，中国全要素生产率增长基本呈稳步上升趋势，2006年达到21．67%的最高水平，尽管2007年和2008年的增长率为负值，但考虑到Hicks－Moorsteen全要素生产率指数的测算以上一年为基准，因此这两个年份全要素生产率的绝对水平仍然是比较高的。中国全要素生产率的增长之所以呈上述变化特征，与环境政策变化密切相关：一方面，随着中国经济发展水平的持续上升，工业化进程中的环境污染问题逐渐得到中央政府的重视，并开始纳入地方政府的政绩考核范围，由此在一定程度上缓解了环境约束；另一方面，重要环境监管政策的制定和实施，直接促进了环境污染问题的解决，这突出体现在《关于落实科学发展观加强环境保护的决定》（国发〔2005〕39号）的颁布，随之出现了2006年全国范围内工业污染物排放量的显著下降，因而带来了全要素生产率的超快增长。但是，目前中国环境问题的解决具有复杂性、艰巨性和长期性，仍缺少长效治理机制，这势必会影响全要素生产率水平，并降低经济增长质量。

第三，从区域情况看，由于工业化进程和经济发展水平的差异，不同省份环境约束程度明显不同，且在区域间和区域内出现了进一步的分化，特别是区域内差异日益突显，对环境监管政策提出了新的挑战。因此，如何统筹中央政府统一政策和地方政府区域政策的制定、实施及评估，激发地方政府治理环境问题的内在动力，促进企业节能减排，将是从根本上缓解环境约束的核心内容。

（二）三大区域结果分析

表2为主要年份三大区域Hicks－Moorsteen全要素生产率指数及其分解结果。

表2 中国三大区域Hicks－Moorsteen全要素生产率指数及其分解结果表

根据表2的估计结果，当考虑了环境约束的影响之后，2000—2008年中国三大区域全要素生产率均保持增长态势，其平均增长率由高到低依次为：东部地区（3．07%）＞西部地区（1．29%）＞中部地区（0．41%）。上述排序结果表明：一方面，由于全要素生产率水平的不同，就经济增长质量而言，东部地区要显著优于中部地区和西部地区，继续保持在经济发展上的绝对优势；另一方面，西部地区经济增长质量明显高于中部地区，与现实中这两大区域的常规经济表现并不完全相同，这可能是环境约束发挥作用的结果。从地区经济的产业结构看，西部地区工业总体上要落后于中部地区，更多的是资源型和劳动密集型产业，所受环境约束明显小于中部地区。

分析三大区域的情况：第一，东部地区全要素生产率主要得益于技术效率的改善，平均增长率为4．39%，其次是技术进步水平的提高，平均增长率为1．26%。东部地区全要素生产率大致呈缓慢增长态势，自2005年起增长速度有所加快，考虑到近年来的现实情况，中国环境监管政策确实起到了积极作用，特别是工业化水平较高的东部地区受到了更多关注。第二，中部地区全要素生产率基本呈缓慢增长态势，从增长来源看，技术效率的贡献略高于技术进步，平均增长率分别为1．66%和1．26%。就演进特征而言，技术效率和技术进步的增长均具有明显的波动性，且二者呈显著的反方向变化。第三，西部地区全要素生产率总体上呈稳步增长态势，这主要是受到技术进步的影响，二者的增长率具有较高的一致性。在增长动力构成方面，技术进步的作用略大于技术效率，平均增长率分别为1．26%和1．14%。

（三）八大综合经济区结果分析

表3是八大综合经济区Hicks－Moorsteen生产率指数及其分解结果。

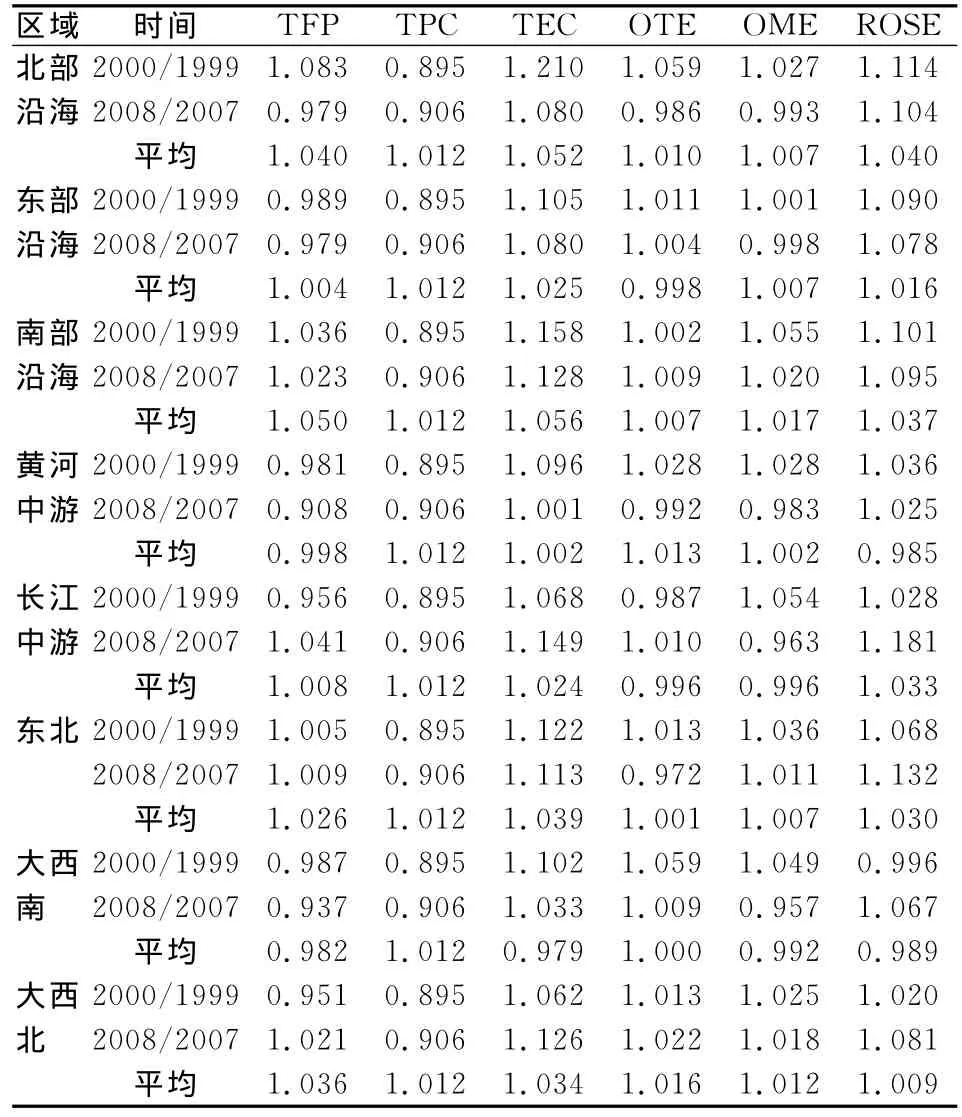
表3 中国八大综合经济区Hicks－Moorsteen全要素生产率及其分解结果表

根据表3的估计结果，把环境约束的影响纳入分析框架之后，黄河中游综合经济区和大西南综合经济区的全要素生产率为负增长，其他六个综合经济区为正增长，按全要素生产率平均增长率从高到低排序：南部沿海综合经济区（5．01%）＞北部沿海综合经济区（4．06%）＞大西北综合经济区（3．61%）＞东北综合经济区（2．66%）＞长江中游综合经济区（0．83%）＞东部沿海综合经济区（0．46%）＞黄河中游综合经济区（－0．17%）＞大西南综合经济区（－1．77%）。考虑环境约束后，中国全要素生产率增长的区域差异特征非常明显，意味着在制定和执行有关旨在解决环境污染问题的政策、制度及措施时，应当充分考虑不同经济区域的具体情况，采取差异化的解决思路，以有效缓解环境约束的影响。

分析各综合经济区：第一，北部沿海综合经济区。全要素生产率的增长先上升后下降，总体上保持较快增长，主要是技术效率的改善，平均增长率为5．25%，技术进步的贡献相对较小，平均增长率为1．26%；第二，东部沿海综合经济区。全要素生产率总体上增长缓慢，并具有一定的波动性特征。技术效率的贡献大于技术进步，平均增长率分别为2．57%和1．26%；第三，南部沿海综合经济区。全要素生产率总体上保持快速增长，在八个综合经济区中增长最快，主要得益于技术效率的显著改善，平均增长率为5．66%，技术进步也起到了积极作用，平均增长率为1．26%；第四，黄河中游综合经济区。全要素生产率为负增长，主要因2007年和2008年的迅速下降，技术进步和技术效率的波动性非常明显，稳定性较差；第五，长江中游综合经济区。全要素生产率总体上呈缓慢增长态势，技术效率的贡献大于技术进步，平均增长率分别为2．41%和1．26%，但二者的增长率均表现出明显的波动性特征，稳定性不强；第六，东北综合经济区。全要素生产率总体上保持了一定的增长速度，并有逐渐加快趋势，主要是技术效率发挥作用的结果，平均增长率为3．99%，同期技术进步也起到了积极作用，平均增长率为1．26%；第七，大西南综合经济区。全要素生产率的平均增长率为负，主要因技术效率在部分年份的迅速下降，在很大程度上抵消了技术进步的拉动作用，二者的平均增长率分别为－2．06%和1．26%；第八，大西北综合经济区。全要素生产率总体上保持较快增长，主要受益于技术效率的改善，平均增长率为3．46%，同时技术进步也起到了积极作用，平均增长率为1．26%。

五、结 论

积极借鉴国际经验、紧密围绕所处的经济发展阶段、探索适合基本国情的经济改革与发展之路、实现社会经济环境可持续发展，是中国经济需要长期面对的重大问题。在研究和解决这一问题的过程中，全要素生产率始终是重要观测指标。因此，在考虑环境约束的基础上，采用Hicks－Moorsteen指数方法，运用省级面板数据具体考察了中国区域全要素生产率的增长情况，并根据实证研究结果得到以下基本结论：环境约束对中国区域全要素生产率增长具有显著影响，并在一定程度上加速了不同区域和各省之间的差异化；2000—2008年中国全要素生产率平均增长率为1．69%，其中技术效率平均增长率为2．43%，技术进步平均增长率为1．26%；从不同区域来看，2000—2008年三大区域全要素生产率平均增长率由高到低依次为：东部地区（3．07%）＞西部地区（1．29%）＞中部地区（0．41%）；八大综合经济区全要素生产率平均增长率由高到低依次为：南部沿海（5．01%）＞北部沿海（4．06%）＞大西北（3．61%）＞东北（2．66%）＞长江中游（0．83%）＞东部沿海（0．46%）＞黄河中游（－0．17%）＞大西南（－1．77%）。

根据以上结论可得到如下政策启示：

第一，应积极采取措施，强化环境保护意识和可持续发展理念，创新环保模式，鼓励和引导企业采用先进可行的环保型生产技术，加大对产中和产后主要污染物排放的处理力度，有计划有步骤地扩大地区和企业覆盖范围，分阶段分层次地缓解环境约束问题；第二，应充分考虑中国不同区域间和区域内环境约束的差异性，注重坚持因地制宜这一基本原则，提高已有环境监管制度和政策的实施效果；第三，应逐步构建解决环境问题的长效机制，特别是中央政府，有必要进一步调整和优化中国有关环境监管方面的制度设计及政策制定，促进地方政府和企业积极参与环境治理的全过程，为从根本上促进环境污染问题的解决奠定坚实基础。

长期以来，对全要素生产率的估算是研究者关注的重要主题，这里有必要强调的是，上述实证分析结果和基本结论仍是初步的，可靠性和严谨性还有待深入研究和论证，这将是笔者今后的研究方向。为进一步检验上述研究结果的可靠性和严谨性，以下研究工作将是必要的：首先，扩大研究样本的时期跨度，更为系统地探讨中国经济发展过程中的环境约束问题以及全要素生产率区域差异的影响；其次，运用同一组分析样本，具体比较Malmquist指数方法和Hicks－Moorsteen指数方法的估计结果，分析可能的差异，为理论检验提供经验证据；最后，从理论上研究环境约束的中国区域全要素生产率增长的影响因素，分析发生作用的内在机理，并进行相应的实证检验，为政策研究提供依据。

［1］ 周茜．中国区域经济增长对环境质量的影响——基于东、中、西部地区环境库兹涅茨曲线的实证研究［J］．统计与信息论坛，2011（10）．

［2］ 张进铭，廖鹏．中国省际全要素能源效率变动分解——基于环境约束条件下的研究［J］．统计与信息论坛，2012（3）．

［3］ 魏玮，宋一弘．环境约束下城市全要素能源效率的变动分解——基于三阶段DEA－malmquist指数的实证分析［J］．统计与信息论坛，2012（9）．

［4］ 许旭，金凤君，刘鹤．产业发展的资源环境效率研究进展［J］．地理科学进展，2010（12）．

［5］ 王兵，吴延瑞，颜鹏飞．中国区域环境效率与环境全要素生产率增长［J］．经济研究，2010（5）．

［6］ 王姗姗，屈小娥．基于环境效应的中国制造业全要素能源效率变动研究［J］．中国人口·资源与环境，2011（8）．

［7］ Fethi M D，Pasiouras F．Assessing Bank Efficiency and Performance With Operational Research and Artificial Intelligence Techniques：A Survey［J］．European Journal of Operational Research，2010（2）．

［8］ Fare R，Grosskopf S，Norris M，et al．Productivity Growth，Technical Progress and Efficiency Changes in Industrialized Countries［J］．American Economic Review，1994（1）．

［9］ Ray S C，Desli E．Productivity Growth，Technical Progress，and Efficiency Change in Industrialized Countries：Comment［J］．American Economic Review，1997（5）．

［10］Grifell－Tatje E，Lovell C A K．A Note on the Malmquist Productivity Index［J］．Economics Letters，1995（2）．

［11］Wheelock D C，Wilson P W．Technical Progress，Inefficiency and Productivity Change in U．S．Banking，1984－1993［J］．Journal of Money，Credit and Banking，1999（2）．

［12］Coelli T J，Rao D S P．Total Factor Productivity Growth in Agriculture：A Malmquist Index Analysis of 93Countries，1980－2000［J］．Agricultural Economics，2005（s1）．

［13］O′Donnell C J．An Aggregate Quantity－price Framework for Measuring and Decomposing Productivity and Profitability Change［R］．CEPA Working Paper，University of Queensland，2008．

［14］Caves D W，Christensen L R，Diewert W E．The Economic Theory of Index Numbers and the Measurement of Input and Output，and Productivity［J］．Econometrica，1982（6）．

［15］Diewert W E．Fisher Ideal Output，Input，and Productivity Indexes Revisited［J］．Journal of Productivity Analysis，1992（3）．

［16］Hicks J R．Measurement of Capital in Relation to the Measurement of Other Economic Aggregates［C］∥ Lutz F A，Hague D C．Theory of Capital．London：Macmillan，1961．

［17］Moorsteen R H．On Measuring Productive Potential and Relative Efficiency［J］．Quarterly Journal of Economics，1961（3）．

［18］Sherphard R W．Cost and Production Functions［M］．Princeton：Princeton University Press，1953．

［19］O′Donnell C J．Measuring and Decomposing Agricultural Productivity and Profitability Change［J］．Australian Journal of Agricultural and Resource Economics，2010（4）．

［20］O′Donnell C J．Nonparametric Estimates of the Components of Productivity and Profitability Change in U．S．Agriculture［R］．CEPA Working Paper，University of Queensland，2010．

［21］胡鞍钢，郑京海，高宇宁，等．考虑环境因素的省级技术效率排名（1999－2005）［J］．经济学，2008（3）．

［22］Hall R，Jones C．Why Do Some Countries Produce So Much More Output Per Worker than Others［J］．Quarterly Journal of Economics，1999（1）．