基于模糊神经网络的教育经济贡献度研究

王 晖，唐 静

(1.湖南农业大学生物科学技术学院，长沙 410128 2.湘潭大学旅游管理学院，湖南 湘潭 411105；3.四川大学 商学院，成都 610064)

基于模糊神经网络的教育经济贡献度研究

王 晖1,2，唐 静3

(1.湖南农业大学生物科学技术学院，长沙 410128 2.湘潭大学旅游管理学院，湖南 湘潭 411105；3.四川大学 商学院，成都 610064)

文章将模糊理论和神经网络理论结合在一起，构建了用于教育经济贡献度分析的实证模型。通过三个阶段的指标选取和神经网络训练，最终的实证结论显示，教育对于我国经济的发展具有明显的促进作用。

模糊理论；神经网络；教育投入；经济增长；贡献度

1 教育经济贡献度评价的模糊神经网络模型

教育对于经济增长的影响，是一个典型的社会问题和经济问题。其复杂性使得一些确定性的数学方法难以适用，甚至很多情况下我们根本无法构建出二者之间关系的确定结构模型。在这种情况下，模糊理论和神经网络方法就比较适用了。尤其是新千年以后，模糊理论在教育经济贡献度评价的研究中应用越来越普遍。基于此，本文将两种方法结合起来，构建一种模糊神经网络评价模型，用于教育经济贡献度的研究。

实证步骤：

首先，构建三个评价参数集合。第一个评价参数集合包括，人均国民生产总值；第二个评价参数集合包括，人均国民生产总值、人均固定资产、人力资本、人均耕地面积；第三个评价参数集合包括，教育资本指标、健康资本指标、经验资本指标、人力资本指标。三个参数集合各有功用，第一个评价参数集合用于对我国各地区进行模糊分类，第二个评价参数集合用于建立人力资本和经济之间的联系，第三个评价参数集合用于建立教育和人力资本之间的联系。

其次，根据神经网络方法和第一个评价参数集合，对我国不同地区的经济发展进行大致分类，因为不同经济水平的地区中，人力资本对于经济的影响力度差异性很大。

再次，针对同一经济水平的区域构建人力资本到经济增长之间的联系模型。对于第二个评价参数集合而言，用G表征人均国民生产总值，分别用q1、q2、q3表征人均固定资产、人力资本、人均耕地面积，几者之间的关系表现为：

根据公式(1)训练出人力资本到经济增长之间的模糊神经网络模型后，人力资本对于经济增长的贡献程度就可以用η来描述。

再次，根据第三个评价参数集合和模糊神经网络训练方法，构建教育资本和人力资本之间的联系。这时，用R代表人力资本，用q1、q2、q3分别表征教育资本指标、健康资本指标、经验资本指标，相关的数学描述为：

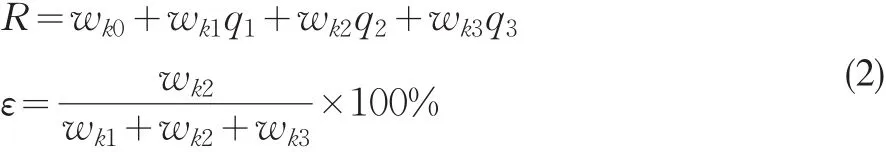
根据公式(2)训练出教育资本对于人力资本之间的模糊神经网络模型后，教育资本对于人力资本的贡献程度就可以用ε来描述。

最后，将两个贡献度参数η和ε相乘，就可以得到教育对于经济增长的贡献程度。

2 教育经济贡献度评价的实证分析

2.1 全国各地区的经济水平划分

全国过各地区经济水平的划分，我们依据了2012年底的全国31个省份的人均GDP情况进行了区域划分。2012年全国31个省份的人均GDP情况如表1所示。

使用Stata 11.0软件对所提取的资料信息进行Meta‐分析。本研究的结局指标为二分类变量，以比值比（OR）及其95%置信区间（95%CI）作为合并效应量。采用Q检验及I2检验对所纳入研究的异质性进行检验，如果P≤0.10或I2＞50%时，表明研究间异质性较大，将采用随机效应模型进行结局指标效应值的合并分析；反之则采用固定效应模型进行合并分析。采用漏斗图定性判断发表偏倚并采用Egger's检验定量判断发表偏倚，P＜0.05时，表明存在发表偏倚。

从表1中的数据可以看出，天津市、北京市、上海市的人均GDP水平最高，形成了第一梯队。对于其它省市，我们以全国人均GDP水平作为分界线。2012年全国人均GDP是38253.52元，这样其上的江苏省、内蒙古自治区、浙江省、辽宁省、广东省、福建省、山东省、吉林省、重庆市、湖北省、陕西省就形成了第二梯队，其下的河北省、宁夏回族自治区、黑龙江省、新疆维吾尔自治区、山西省、湖南省、青海省、海南省、河南省、四川省、江西省、安徽省、广西壮族自治区、西藏自治区、云南省、甘肃省、贵州省就成为第三梯队。对于三个水平层次的区域，我们分别进行三个模糊神经网络的训练。

表1 2012年全国31个省份的相关数据

2.2 人力资本对于经济增长的贡献度

进行了经济水平划分手，我们分别在三个层次的省份里训练网络，并依据公式(1)建立人力资本和经济增长之间的关系，具体的训练数据如表1所示。在表1中，除了人均国民生产总值以外，我们还分别统计了人均固定资产、人均耕地面积和人力资本。之后通过公式(1)所述的方法进行计算，得到的具体数值如表2。

表2 人力资本对于经济增长的模糊神经网络训练结果

从以上分析结果可以看出，人力资本对于经济贡献度对于不同经济水平地区都具有很大的作用，对于第一水平层次的省份，贡献度为45.76%；对于第二水平层次的省份，贡献度为48.58%；对于第三水平层次的省份，贡献度高达63.97%。这说明，经济水平越不发达，人力资本的提高越可以起到有效的促进作用。

2.3 教育对于人力资本的贡献度

下面再来分析教育对于人力资本的贡献程度，用于分析的第三层次参数数据如表3所示。

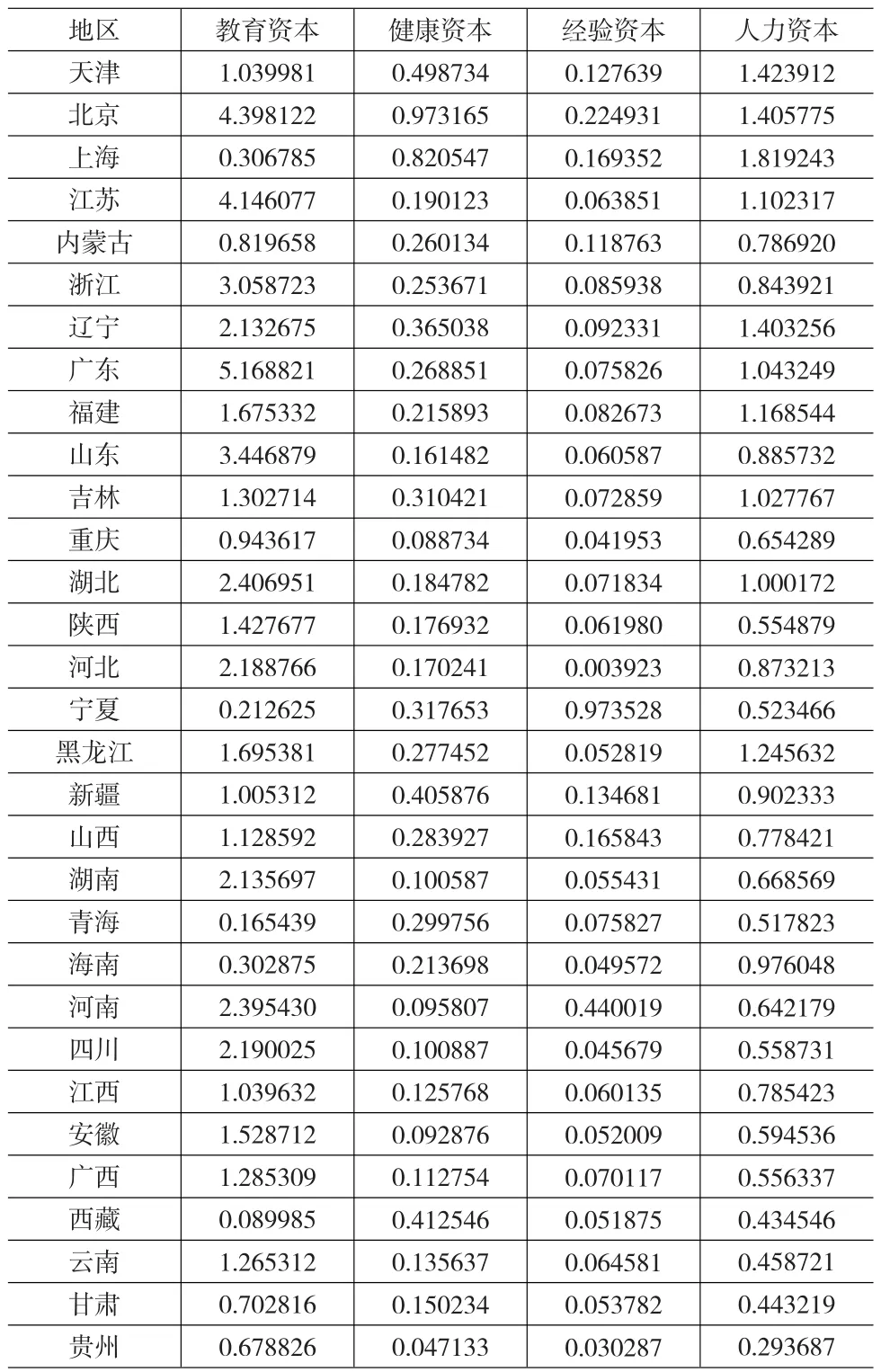
表3 第三层次参数数据

依据公式(2)，进一步推算教育资本对于人力资本的贡献度如表4所示。

从以上分析结果可以看出，教育投入对人力资本贡献度对于不同经济水平地区都具有很大的作用，对于第一水平层次的省份，贡献度为25.31%；对于第二水平层次的省份，贡献度为29.30%；对于第三水平层次的省份，贡献度高达41.57%。这说明，经济水平越不发达，教育对于人力资本的提升具有更大的作用。

2.4 教育对于经济增长的贡献度

综合两步实证分析的结果，综合求取教育对经济增长的贡献度如表5所示。

表5的数据直观地反映了我国教育对于经济增长的贡献，对于发达经济省份，贡献率为11.58%；对于中等经济省份，贡献率为14.23%；对于落后经济省份，贡献率为28.83%。

表4 教育对于人力资本的模糊神经网络训练结果

表5 教育对经济增长的贡献度

3 结论

本文以教育对于经济的贡献度为核心研究目标，构建了基于模糊神经网络的实证分析模型，并明确了具体的执行步骤。实证分析过程中，通过三个阶段评价参数的选取，通过执行模糊神经网络的迭代过程，最终获得了有关的实证结果。实证结果显示，对于我国不同经济水平的地区，教育都通过提生人力资本的素质，达成了对经济增长的促进作用。其中发达经济省份的影响小些，落后经济省份的影响大些。这说明，对于落后经济省份，必须通过教育提高人的素质，来最终实现跨越式的经济发展。

参考模型：

[1]韩宗礼.我国教育投资的经济效益探析[J].教育研究,2010,11(2).

[2]崔玉平.教育对经济增长贡献率的估算方法综述[J].清华大学教育研究,2009,25(1).

[3]安雪慧.教育经济效益计量方法分析[J].高等师范教育研究,2011,11(3).

[4]赖得胜.对教育经济增长的一个交易费用经济学解释[J].学术研究,2007,21(9).

[5]王家赠.教育对中国经济增长的影响分析[J].上海经济研究,2012,33(2).

[6]史清琪,秦宝庭,陈警.中国经济增长因素分析[M].北京:科学技术文献出版社,2012.

[7]苗庆红.教育经济增长贡献计量方法中的一些问题[J].教育经济,2012,24(5).

F062.2

A

1002-6487（2013）14-0111-03

教育部人文社会科学研究项目（10YJC790039）；湖南省教育厅教学改革项目（湘教通[2012]401号）

王 晖（1978-），女，河北献县人，博士研究生，讲师，研究方向：生态经济、服务管理。

（责任编辑/亦 民）