基于应变的复合材料Non-Fickian吸湿方程

韩坤华， 余 音， 汪 海

(上海交通大学航空航天学院，民机结构强度综合实验室，上海200240)

0 引言

先进复合材料应用于飞机结构要承受温度、湿度与载荷联合作用的严酷外部环境因素，而复合材料由于其聚合物基体的极性，容易在潮湿环境下吸湿，使其性能退化，进而降低复合材料力学性能［1-2］。国内外学者都十分重视对复合材料在湿热环境下的力学行为研究，并将湿热环境对于复合材料力学性能的影响作为衡量复合材料耐久性的首要因素，而在湿度、温度与外载荷的联合作用下，复合材料的吸湿行为愈显复杂。更多的研究［3-7］表明，复合材料的复杂吸湿行为已经偏离了Fick扩散，表现出Non-Fickian行为。Fahmy等［8］发现应力会影响复合材料的吸湿过程，其4点弯曲试验表明，试样的受拉面比受压面的吸湿量更多。随后，Neumann等［9］指出控制湿-力耦合的力学变量是应变而不是应力。Lee等［10］研究了基于湿浓度和基于应力的湿扩散方程，结果表明吸湿会在试样中心引起横向拉应力，在表面引起横向压应力，扩散率会由于拉应力而增加，材料表面的吸湿快于中面。但是该研究所建立的耦合方程中，是靠经验常数使2个变量相互作用的，常数的选择依赖于吸湿试验。Samit Roy等［11-13］基于连续介质力学与热力学第二定律，采用Gibb自由能的特殊形式，将应力、温度与湿度作为独立的场变量建立了正交各向异性材料在应力、温度与吸湿历程间相互作用下的吸湿控制方程。该方程形式复杂，参数多，不能有效地用于工程计算。但是其理论方程对于研究材料在湿热载复杂环境下的吸湿历程很有价值，研究表明，短时间内，Fick定律会过高估计材料的吸湿量，在有外力或者存在应变时，Fick定律不再适于描述材料的吸湿行为。

本文根据复合材料层压板吸湿试验中所表现出的Non-Fickian行为，建立基于应变的湿扩散方程，计入湿浓度与应变的耦合作用，得到不同时刻层压板内部的瞬态湿浓度分布，并根据经典层压板理论计算层压板内由于受热和吸湿引起的湿热残余应力。所建立的方程不需引入经验常数，适合于计算不同材料、铺层、厚度及不同环境条件下的复合材料层压板试验件的吸湿量，计算结果比传统Fickian扩散更接近于试验结果。

1 复合材料层压板的吸湿试验

试验选取不同厚度、不同材料的复合材料单向层压板与多向层压板试验件，在不同的环境处理条件下分别做吸湿试验。环境箱采用ETH-225-70-CP-AR可程式恒温恒湿试验机，其温度控制范围是－70～150°C，相对湿度(Relative Humidity，RH)范围是10% ～98%，温湿度控制精度为 ±0.2 °C，±2.5%RH。试验参照ASTM D 5229标准［14］进行，试验参数见表1。

试验件吸湿百分比-时间曲线的试验结果如图1所示，并将之与Fick方程［16］的计算结果进行比较。

表1 复合材料层压板吸湿试验件

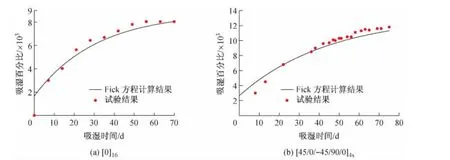
图1 层压板吸湿的试验曲线与Fickian扩散结果比较

由图1可以看出，Fick方程在吸湿初始阶段会过高估计层压板内吸湿量，而在随后的吸湿过程中又过低估计了层压板的吸湿量［10，15］，在复合材料多向板中变现得更明显。因为复合材料单向板的湿热膨胀系数是各向异性，多向层压板相邻层的纤维铺设角不同，势必会在层压板内部引起更大的湿热应力。对此，本文建立基于应变的湿扩散方程，研究复合材料层压板的Non-Fickian吸湿行为。

2 基于应变的湿扩散方程

2.1 复合材料的湿扩散

由于试验件厚度方向的平面面积远大于其他2个平面，所以将复合材料层压板的吸湿简化为一维湿扩散，如图2所示。

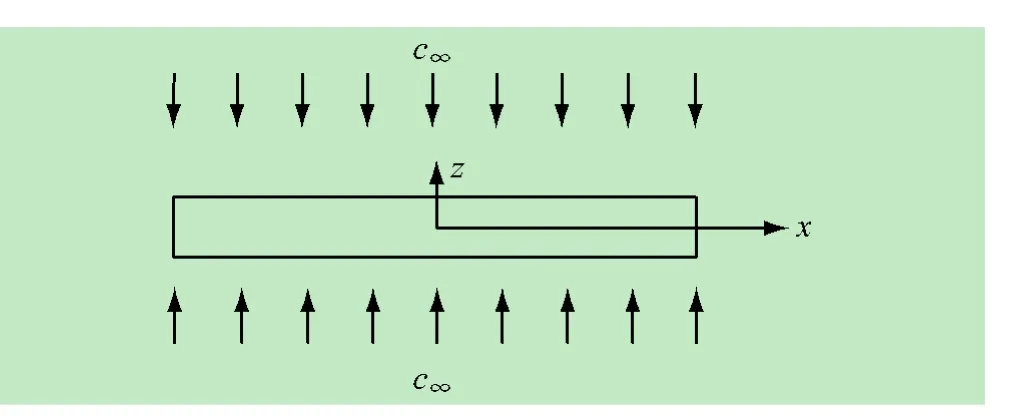
图2 复合材料一维湿扩散

沿厚度的一维湿扩散Fick方程:

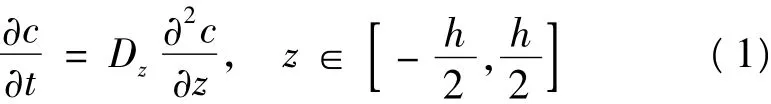
式中:Dz是材料沿厚度方向的扩散率;c是水分比浓度;t是时间;z是厚度方向坐标;h是层压板总厚度。

假设环境中湿浓度为常数c∞，则解上述二阶偏微分方程的初始条件与边界条件为

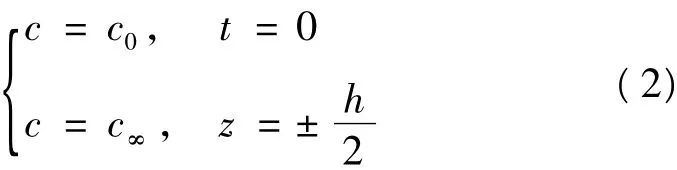
层压板中每一点上的湿浓度是厚度方向坐标与时间的函数，即c(zk，t)，由混合边界条件(2)得到方程(1)的解为

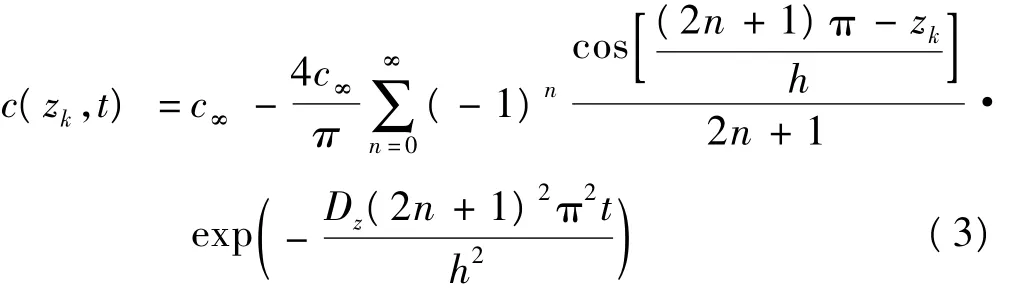
2.2 复合材料层压板中的湿热残余应力

在环境箱内进行吸湿处理的复合材料层压板试验件会因为温度与吸湿而产生湿热内应力。材料达到热稳态的时间远远大于达到湿饱和状态［17］，所以在计算湿热残余应变时认为材料首先已经达到了热稳态，直接加上温度差以后再计算湿扩散过程和吸湿过程中产生的湿热应变与应力。

将复合材料单向层压板简化为平面应力状态，湿度场与温度场存在时其本构关系为

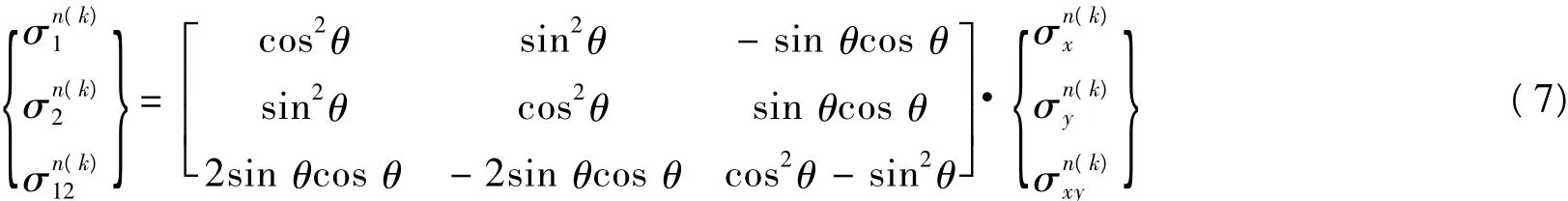
层压板内仅由湿热项引起的面内湿热力与湿热力矩分别为:

由此，可以计算层压板中面应变{εn(0)}与弯曲应变{κn}:

2.3 基于应变的湿扩散方程

在分析层压板内应变时发现，其在吸湿过程中产生的湿热应变以横向ε22最大，其随着时间增长，并与时间的平方根呈线性变化，同吸湿百分比M与时间t的变化趋势一致，如图3所示。

由图3，假设层压板中湿热应变与湿浓度一样，也具有“扩散”功能，并且会对层压板的吸湿产生作用。

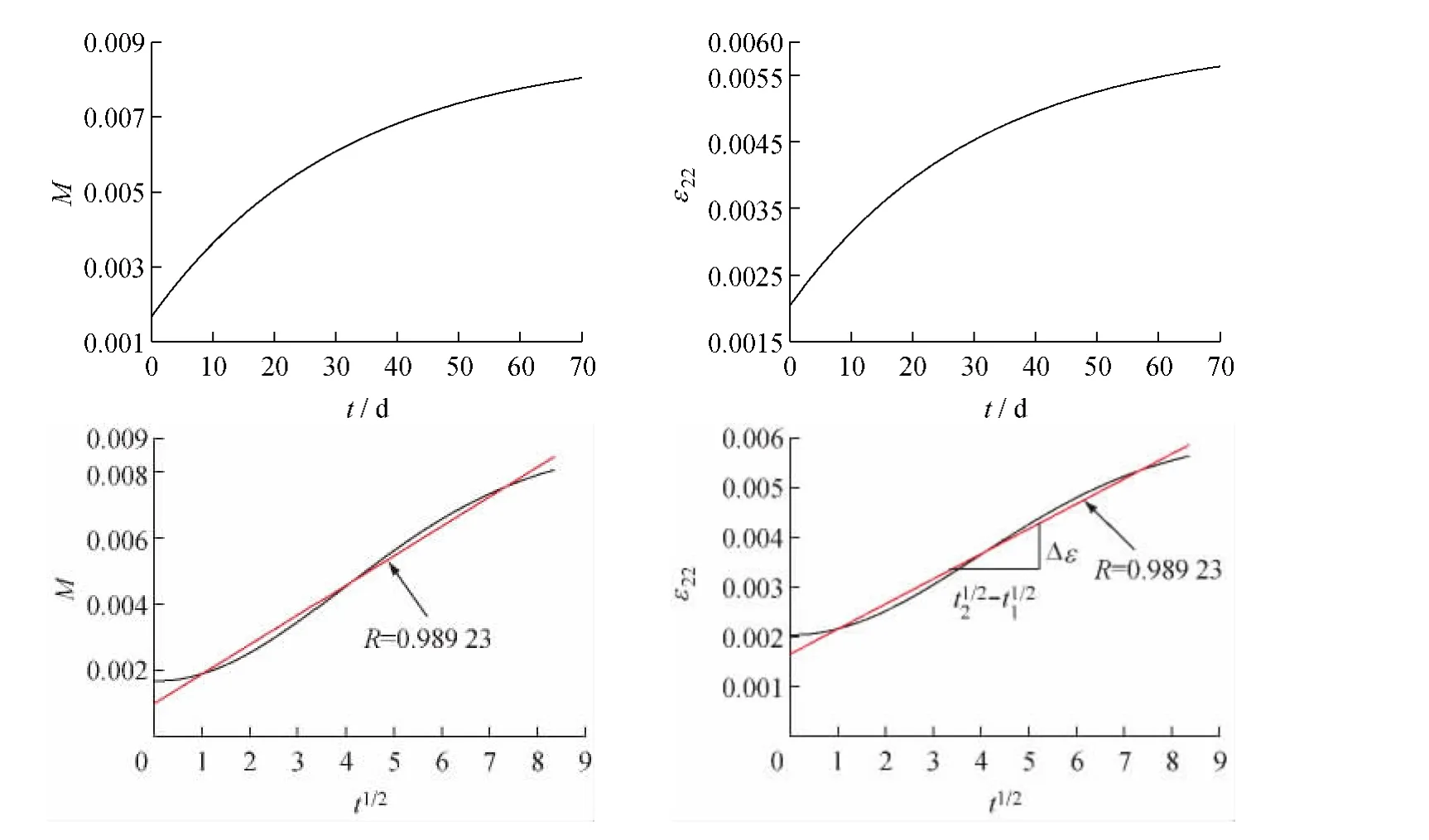
图3 层压板内的湿热应变

仿照计算湿扩散率的公式，也可以计算出相应的应变扩散系数DE，

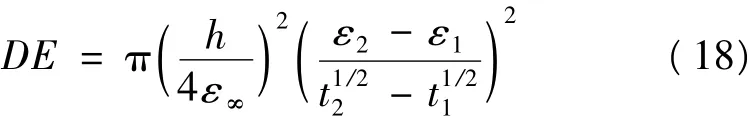
基于计算出的DE在Fick方程中引入应变扩散系数与应变耦合项，建立基于应变的湿扩散-应变耦合方程，

由于此时c与ε22相互耦合，较难推导出解析解，需要利用数值方法解出方程。采取有限差分方法对空间变量采取中心差分法，对于时间变量采取向前差分法。由于向前差分是二阶精度，故必须满足下式的条件才能保证计算收敛:

令空间变量的增量为Δz，时间变量的增量为Δt，则

综上，基于应变的湿扩散-应变耦合计算的流程见图4。

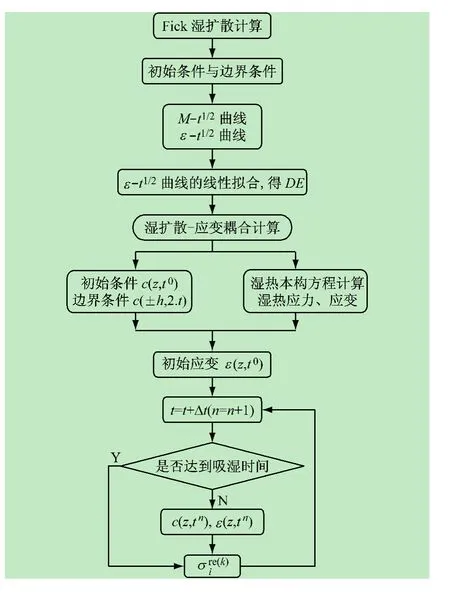
图4 湿扩散-应变耦合计算流程

根据所建立的湿扩散-应变方程重新计算复合材料层压板试验件的吸湿，并与试验结果、Fick扩散结果进行比较，如图5所示。

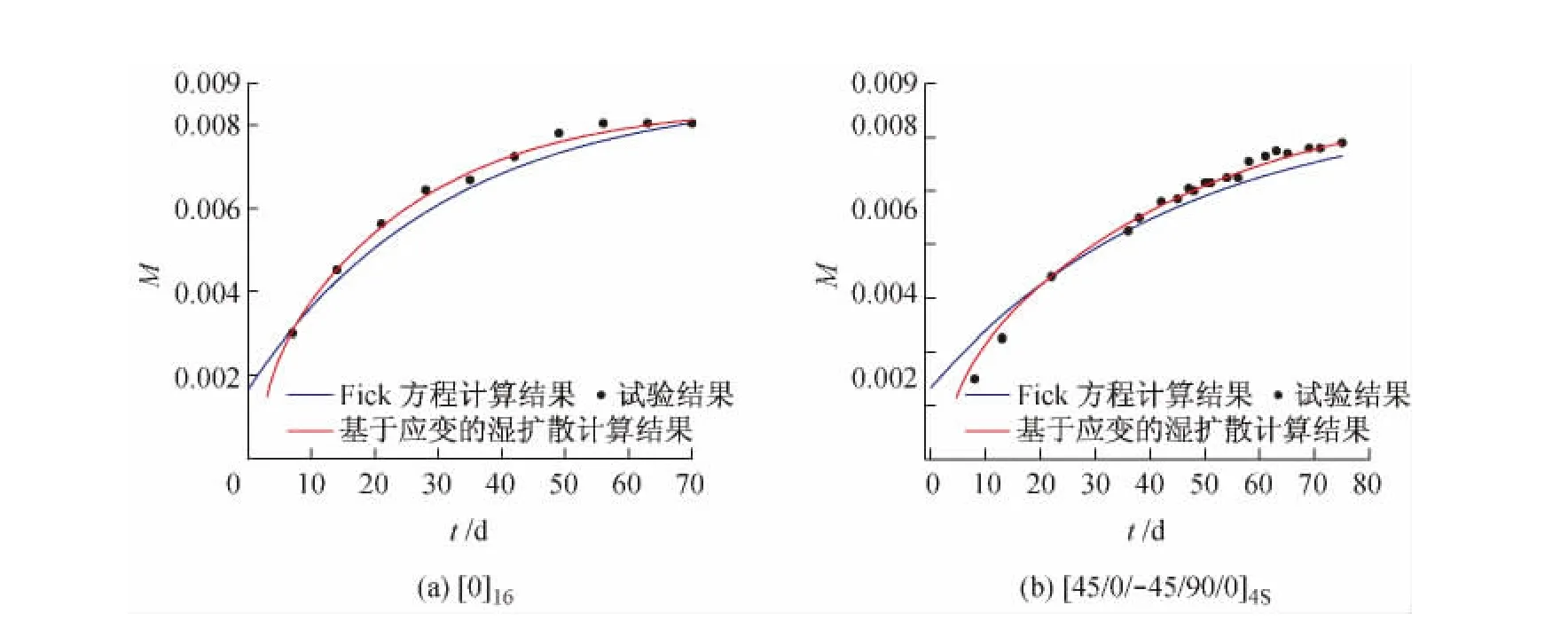
图5 层压板吸湿百分比-时间曲线

由图5可以看出，基于应变的耦合方程在吸湿初始阶段有效地改善了Fick方程过分估计材料吸湿量的情况，在随后的吸湿中，又改善了Fick方程过低估计材料吸湿能力的情况，实验数据点多落于基于应变的耦合湿扩散曲线上，证明材料的吸湿曲线会受到层压板内应变的影响。

以［0］16为例，选取 3 个典型时间点 0.1tmax，0.5tmax，tmax计算单向层压板内横向湿热残余应力，发现耦合的计算结果要略大于非耦合结果，如图6所示。因为，此时应变与扩散率之间有了正影响关系，应变增加扩散率的同时，同一时刻吸湿量的增加也增大了湿热残余应力。

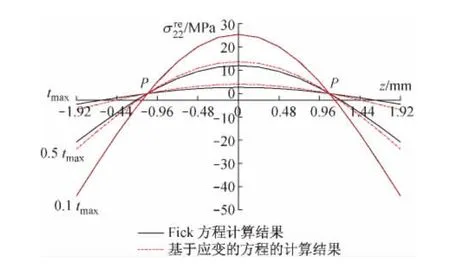
图6 层压板内沿厚度方向分布的横向湿热残余应力

图6 表明在吸湿初始阶段，试样湿扩散方向上存在湿浓度梯度，从而导致该方向上的湿热残余应力也呈梯度分布，单向层压板试样边缘处的横向湿热残余应力达到44.1 MPa，这与基体横向压缩强度相比不可忽略，其可能会引起横向初始裂纹。随着试样吸湿平衡，材料内的湿浓度分布趋于平衡，湿热残余应力分布也趋于平衡。0°单向板由于相邻铺层相同，且处于自由边界条件，所以层压板内最后残余的应力值接近于0。另外，从图6中还能发现这样的现象，不同时刻层压板内的应力分布一直在变化，但是应力分布曲线在变化的过程中有一个不变的交点，如图6中的点P。并且当层压板内应力分布趋于平衡时，残余应力的值就是该交点对应的应力值。由此，就可以通过吸湿初始时两条应力曲线的变化初步估计吸湿饱和时层压板内的残余应力值，大大减少计算代价。

综上，本文所建立的基于应变的湿扩散方程计算结果与试验结果符合良好，并且具有以下优点:

(1)方程中没有经验系数，不需要通过试验数据来拟合，通过Fick扩散计算后得到应变扩散系数DE，再通过耦合方程计算得到复合材料层压板最终的吸湿曲线;

(2)方程中引入了应变耦合项，当复合材料受外载荷而有初始应变场或者吸湿过程中产生内应变时，可以实现湿扩散与应变的相互耦合，更准确地描述湿热载环境下复合材料的吸湿过程;

(3)二阶偏微分方程可以通过有限差分法计算，计算程序简便快捷，效率高。

3 结语

本文通过观察试验中复合材料所表现出的Non-Fickian扩散行为，建立了基于应变的湿扩散方程，并可以得到以下结论:①复合材料的湿扩散与应变间存在完全耦合关系，在研究复合材料吸湿时不能忽略。用本文建立的基于应变的湿扩散方程可以定量描述这种耦合关系，有效改进Fick方程初始时过高估计吸湿量和较长时间后过低估计吸湿量的问题，得到与试验曲线一致的结果;②同一时刻复合材料内湿含量的差距会导致其内部湿热应力分布的差异，耦合计算得到的湿热残余应力值较大，其可能会引起基体内的初始损伤，是复合材料结构设计中需要考虑的重要因素。

［1］ 吕新颖，江 龙，闫 亮，等.碳纤维复合材料湿热性能研究进展［J］.玻璃钢/复合材料，2009(3):76-80.

［2］ 冯 青，李 敏，顾轶卓，等.不同湿热条件下碳纤维/环氧复合材料湿热性能实验研究［J］.复合材料学报，2010，27(6):16-20.

［3］ Loh W K，Crocombe A D，Wahab M M A，et al.Modeling anomalousmoisture uptake，swelling and thermal characteristics of a rubber toughened epoxy adhesive［J］.International Journal of Adhesion and Adhesives，2005，25(1):1-12.

［4］ Derrien K，Gilormini P.The effect of applied stresses on the equilibrium moisture content in polymers［J］.Scripta Materialia，2007，56(4):297-299.

［5］ Fan X J，Lee SW R，Han Q.Experimental investigationsandmodel study of moisture behaviors in polymetric materials［J］.Microelectronics Reliability，2009，49(8):861-871.

［6］ Boualem N，Sereir Z.Accelerated aging of unidirectional hybrid composites under the long-term elevated temperature and moisture concentration［J］.Theoretical and Applied Fracture Mechanics，2011，55(1):68-75.

［7］ Zafar A，Bertocco F，Thomsen JS，et al.Investigation of the long term effects ofmoisture on carbon fiber and epoxymatrix composites［J］.Composites Science and Technology，2012，72(6):656-666.

［8］ Fahmy A A，Hurt JC.Stress dependence ofwater diffusion in epoxy resin［J］.Polymer composites I，1980，1(2):77-80.

［9］ Neumann S，Marom G.Prediction ofmoisture diffusion parameters in compositematerialsunder stress［J］.Journal of Composite Materials，1987，21(1):68-80.

［10］ Lee M C，Peppas N A.Models ofmoisture transport and moistureinduced stresses in epoxy composite［J］.Journal of Composite Materials，1993，27(12):1146-1171.

［11］ Roy S. Modeling of anomalous moisture diffusion in polymer composites:A finite element approach［J］.Journal of Composite Materials，1999，33(14):1318-1343.

［12］ Roy S，Xu W X，Park S J，et al.Anomalousmoisture diffusion in viscoelastic polymers:Modeling and testing［J］.Journal of Applied Mechanics，2000，67(2):391-396.

［13］ Roy S，Vengadassalam K，Wang Y，et al.Characterization and modeling of strain assisted diffusion in an epoxy adhesive layer［J］.International Journal of Solids and Structures，2006，43(1):27-52.

［14］ ASTM D5229/D5229M-92(Reapproved 2010)， Standard test method for moisture absorption properties and equilibrium conditioning of polymermatrix compositematerials［S］.

［15］ Youssef G，Freour S，Jacquemin F.Stress-dependent moisture diffusion in compositematerials［J］.Journal of Composite Materials，2009，43(15):1621-1637.

［16］ Benkeddad A，Tounsi A and Adda-Bedia E A.Effectof temperature and humidity on transient hygrothermal stresses during moisture desorption in laminated composite plates［J］.Composite Structure，2008，82(4):629-635.

［17］ Vaddadi P，Nakamura T，Singh R P.Transient hygrothermal stresses in fiber reinforced composites: a heterogeneous characterization approach［J］.Composites:Part A，2003，34(8):719-730.