基于Gröbner基的圆薄板非线性大挠度分析

张迅炜，周建方，徐吉良

ZHANG Xun-wei, ZHOU Jian-fang, XU Ji-liang

(河海大学 机电工程学院，常州 213022)

0 引言

由于重量轻，易加工，又可承受较大的载荷，薄板结构在工程中使用广泛。为了准确地评估其工作性能，常常需要考察薄板在载荷作用下的力学行为，圆薄板非线性大挠度弯曲就是其中的一个重要问题。

圆薄板大挠度弯曲问题有多种数学模型，其中卡门（Von Karman）方程组由于形式相对简单，又合理地考虑了非线性效应，因而得到广泛采纳。该方程组包括一对耦合的非线性偏微分方程，各国学者对其求解方法进行了大量研究[1～5]。Vincent[1]以载荷为摄动参数，首先求解了均布载荷作用下的圆板大挠度弯曲问题，结果的误差较大。钱伟长[2,3]以中心位移为摄动参数求解了同样的问题，计算结果非常接近实验值，并且求解过程比Vincent的方法收敛更快。叶开沅等改进了摄动法的计算程序，提出了修正迭代法[4]，使得各阶摄动方程不再耦合，计算过程得到较大简化。上述方法均需要多次迭代求解微分方程组，以逐步提高近似解的精度，这要求工程设计人员有较高的数学分析和运算能力，不便于工程应用。

变分法不直接求解卡门方程组，而是将大挠度弯曲问题转化为等价的弹性势能极值问题，通过选取适当的挠曲面函数，得到一个代数方程组，进而求出近似解，求解过程的数学分析较为简便。但是，当挠曲面函数待定系数增多时，将形成多元高次非线性代数方程组。常用的数值方法[6]，如Newton-raphson迭代法，需要给出好的初始值才能保证非线性方程组的收敛。而解析法中的Gröbner基法[7]，通过将一组非线性多项式方程化简为一个等价的三角化方程组，可求得封闭形式的解析解，不会产生增根或少根，能够最大限度地满足方程组的求解精度，克服了数值方法的不足。

本文根据能量原理，用里茨法推出等厚度轴对称圆薄板非线性弯曲问题的变分列式，结合符号计算软件Mathematica，应用Gröbner基法求解了非线性方程组，得到了圆薄板受均布载荷时的最大挠度。结果表明，采用Gröbner基法求解大挠度问题，计算效率较高，且能求得高精度的近似解。

1 里茨法变分列式

在轴对称分布载荷作用下，圆薄板大挠度弯曲时，板的形变势能Vε包括弯曲形变势能Vε1和中面应变势能：

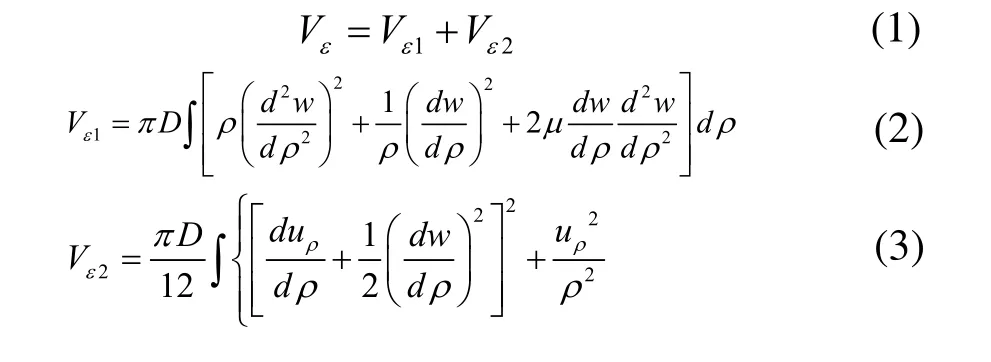
其中， ρ为极坐标；w为板的中面挠度方程；uρ为中面内点的径向位移；μ为泊松比；弯曲刚度，式中：δ为板厚，E为弹性模量。

周边固支时，板的位移边界条件及轴对称条件分别为：

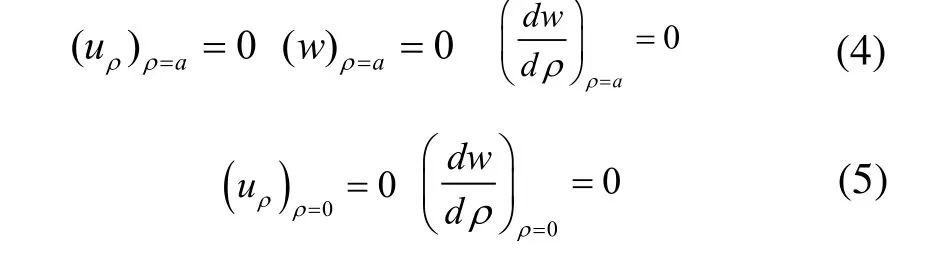
应用里茨法求解时，要求假设的位移函数同时满足式（2）、（3），因此将中面内各点的径向与轴向位移分别取为：

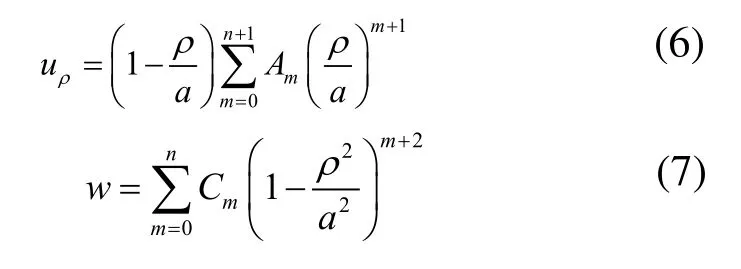
其中，Am、Cm为互不依赖的待定系数；n为非负整数。

根据最小势能原理，圆薄板轴对称弯曲问题的解应满足下列二组方程：

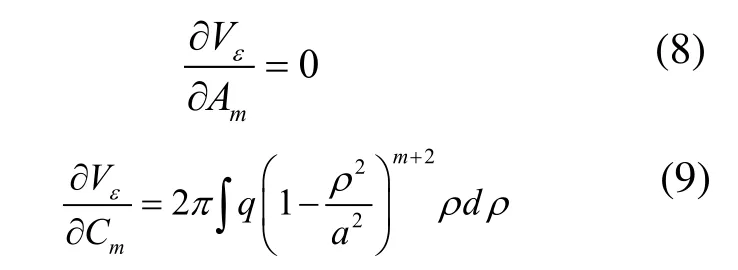
其中，q为载荷集度；

假设式(6)、(7)中的参数值n，并代入式(8)、(9)，得到一个关于Am与Cm的非线性方程组，它包括2n+1个方程。将该方程组的解代入式(6)、(7)即得到板中面各点的径向与轴向位移的近似解，据此可进一步求出应力、内力等其他未知量。随着参数n取值的增大，待定系数的数量相应增加，各级近似解将不断趋近于精确解。

2 Gröbner基法简介与求解步骤

Gröbner基法[9]是一种建立非线性多项式系统标准基的理论和方法。与求解线性方程组的高斯消去法思路相类似，Gröbner基法将非线性系统转化为等价的三角形方程组，从而可用回代的方法求解。该方法在原非线性多项式系统所构成的多项式环内，通过对多项式变元的适当排序，求多项式系统中多项式对的S-多项式，并进行彼此的消元，最终生成一个与原系统完全等价的标准基。Buchberger算法是构造多项式系统Gröbner基的一种有效算法，在计算代数系统（如Mathematica等）中该算法及其改进版本均已实现，可直接以函数方式调用。

本文用改进的Buchberger算法对式(8)、(9)组成的非线性方程组进行求解，步骤为：

1) 假设n，得到关于Am与Cm的非线性方程组G；

2) 将G中所有多项式赋于H；

3) 确定H中的变元的字典法排序，如

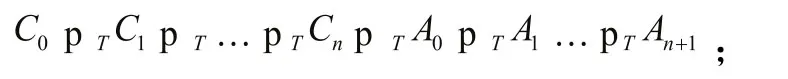
4) 用Gröbner基函数将H化为最简Gröbner标准基，进而得到与原多项式方程组等价的三角化方程组：

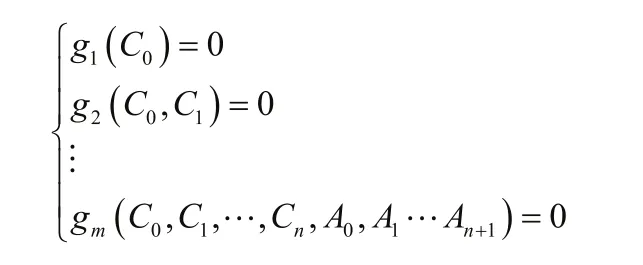
5) 求解其中一元多次方程得到C0，回代方程逐个求出其它变元。

3 算例与程序

设等厚度轴对称圆板，半径为a=2m，厚度为 δ= 0.03m ，受均布载荷作用，周边固支，材料的弹性模量 E= 200GPa，泊松比μ= 0.3，如图1所示。求圆板的最大挠度。

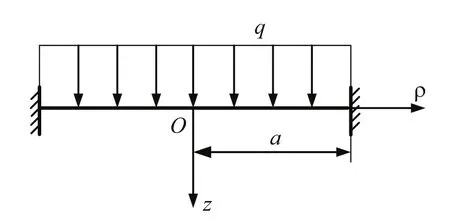
图1 周边固支轴对称圆薄板

由式(7)可知，ρ=0时圆板的中心挠度也就是最大挠度

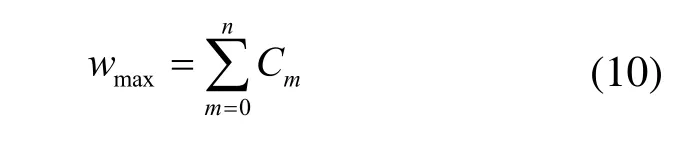
设n=0，式（6）、（7）分别表示为：

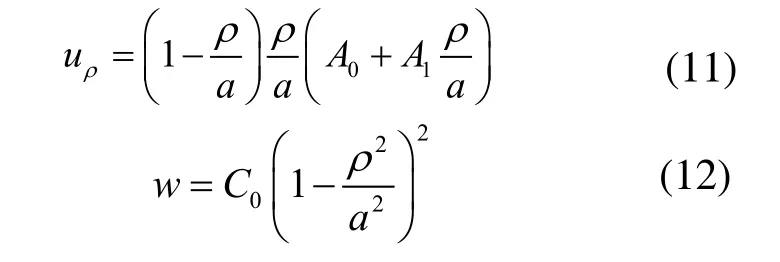
将式(11)、(12)代入式（1）（2）（3），得到形变势能Vε表达式，再代入式（8）、（9）得到非线性方程组：

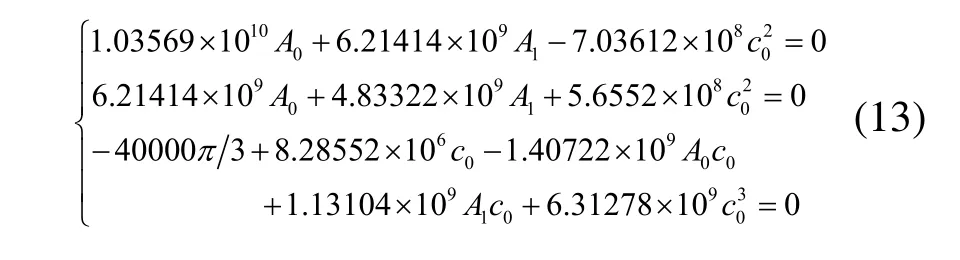
应用Gröbner基法，按前述步骤求解并转换得到的等价三角化方程组为：

由式(14)的第一个方程式可求得C0的三个根。其中唯一的实根，据式（10），就是n取0时板的最大挠度：

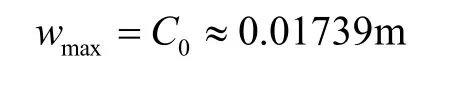
再设n=1，则：

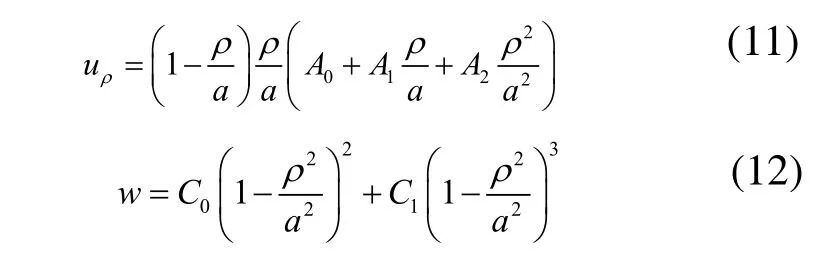
类似地，求得最大挠度：

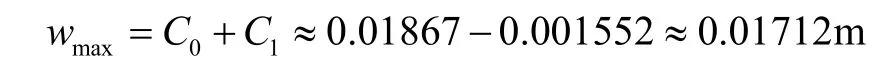
n取不同值时，求解Gröbner基和最大挠度的Mathematica程序如下：

为了检验Gröbner基法以及Mathematica程序的求解精度，对算例中的q取不同值，求得最大挠度wmax，结果汇总于表1。

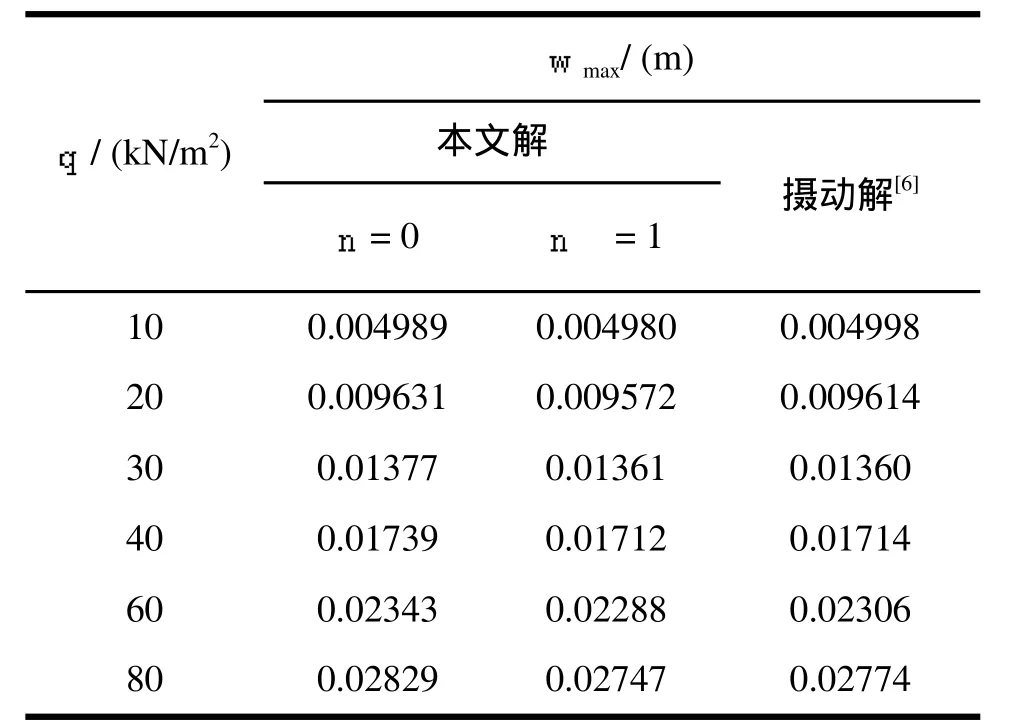
表1 不同载荷集度q下的最大挠度比较

计算结果表明：1）应用里兹法和Gröbner基法求解等厚度圆薄板最大挠度，计算过程收敛速度快，n= 0时，与最大挠度摄动解的误差不超过2%。2）随着参数n的增大，中面各点的位移表达式待定系数相应增加，n=1时，最大误差减小为0.97%，最大挠度更加趋近于摄动解，且结果已能达到工程应用的精度要求。

4 结束语

根据能量原理，本文结合里茨法和Gröbner基法，应用符号计算软件Mathematica求解了等厚度圆薄板的大挠度问题。该方法原理清晰，求解步骤易于编程实现，无需应用复杂的数学分析方法和技巧，就可得到结果的解析符号表达式，或者代入参数求出高精度的数值结果，便于工程应用。本文的方法和程序可推广到其它载荷与约束条件下圆薄板的轴对称大挠度弯曲问题。

[1]Vincent J.J.The bending of a thin circular plate[J].Phil.Mag.,1931,12：185-196.

[2]Chien Weizang.Large deflection of a circular plate under uniform pressure[J].Chinese J.Phys., 1947, 7(2)：102-113.

[3]钱伟长,叶开沅.圆薄板大挠度问题[J].物理学报,1954,10(3),209-238.

[4]叶开沅,刘人怀,李思来,平庆元.在对称线布载荷下的圆底扁球壳的非线性稳定问题[J],兰州大学学报,1965,18(2)：10-33.

[5]孙文俊.求大挠度板高级变分近似解的一种算法[J].河海大学学报,1990,18(2)：20-24.

[6]冯果忱.非线性方程组解法[M].上海：上海科学技术出版社,1989.

[7]刘木兰.Gröbner基理论及其应用[M].北京：科学出版社,2000.

[8]徐芝纶.弹性力学[M].第4版.北京：高等教育出版社,2006.