基于ABAQUS的重力活塞取样器理论分析与研究

徐 建，孟广耀

青岛理工大学机械工程学院，山东青岛 266033

1．Introduction

The 21st century is the century belonging to the ocean on marine scientific investigation，and the study of seafloor sediments becomes the focus of marine research［1］．China’s seabed sampling equipment is generally modeled on the Russian equipment and sampling depth is usually less than 20 m［2］．With the development of China’s Marine Programs，present sampling depth can not satisfy the task of the expedition．Due to the late start of the development and utilization of ocean，the marine seabed sampling is generally modeled on the foreign corers．The theoretical research and experimental validation of seabed sampling design seriously restricts the development and utilization of marine in China［3］．

1．1．The summarization and composition of gravity piston corer

Currently，seabed sampling mainly utilizes gravity-based and piston-structured gravity piston corer［4］，which is widely used in the sediment sampling of the deeper lakes，oceans and other places．It mainly consists of rope fixture，releaser，stripping tube head，and rudder，attached lead weights，connecting flange，sampling tube，seal，and attached hammer and so on，as shown in Fig．1．

Fig．1 Composition of the gravity piston corer

1．2．Gravity piston corer work process

The work process of a gravity piston corer is divided into four steps:overall down，release sampling tube，sampling tube sampling，sampler recover，as shown in Fig．2．

According to the sampling depth and the depth of the seabed in the course of work，the length of the attached hammer and rope will be adjusted，respec-tively，on the side of the ship so that the corer and the attached hammer fall in parallel and vertical direction．Due to the interaction of gravity and seawater buoyancy force，the corer will reach the seabed with a certain constant velocity．Once the sampling vessel is about to reach the seabed，the attached hammer will first contact with the seabed，and then the releasing device will release the sampling tube．Due to the effect of rudder，the sampling tube will fall smoothly in a certain velocity until down deeply into the seabed．At this moment，under the pressure of the sediment，the incision of the sampling pipe will completely open and the sediment will be poured into the sampling tube．When the corer stops sinking，the wire rope on the boat will be pulled to recover the corer．Due to the gravity of the sediment in the sampling tube，the corer blade will be automatically closed with sediments and the sampling work is completed［5］．

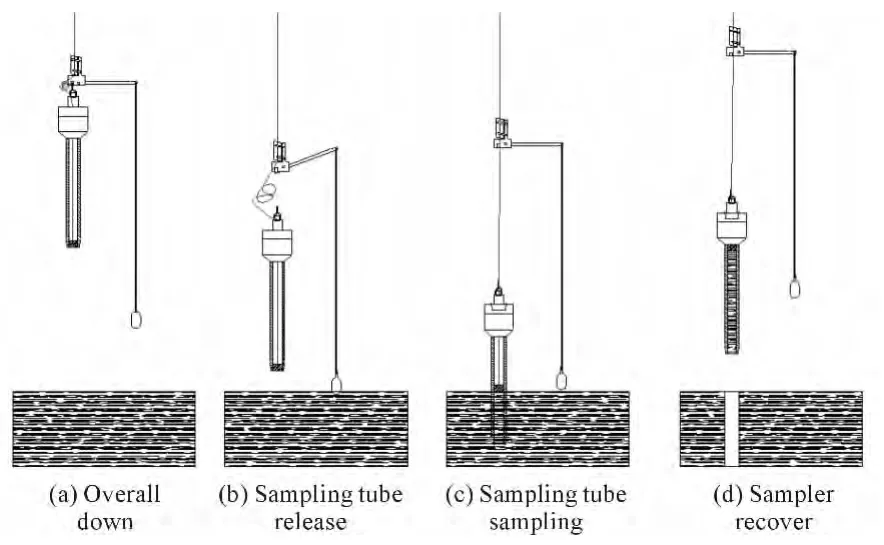
Fig．2 Corer work process

2．Establishment of corer penetration depth theoretical model

Before the theoretical calculations，some assumptions are made as follows:

1)Gravity piston corer will not be shedding during falling process and it will continue to sink at a certain velocity until it reaches a certain depth．

2)During the descent of the gravity piston corer，seawater flow is stationary，which means the corer will not be tilted or affected in the rate of declining by seawater undercurrent．

3)Ignore influences of the resistance from large stones or gravel when the corer enters into sedimentary．i．e．，the entire dropping and penetration process are under ideal condition．

2．1．Penetration depth equation

The initial kinetic energy Ek=mv2is taken into account when a corer falls from a certain height．The friction f=πgl from the seafloor sediment and sampling tube wall in the sampling process will be considered through the friction force A= πcg∫l0l d l=τcgl2．If the corer stops penetrating at the depth of l from the sediment surface，the potential energy at the sediment surface is:Ep=mgl

Based on the principle of conservation of energy，the following equation could be obtained:A-Ep-Ek=0，and then it becomes:

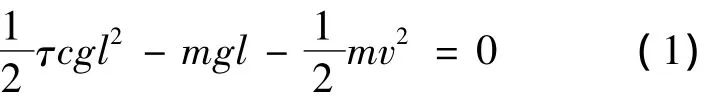
Solve Eq．(1)for l，one could obtain:

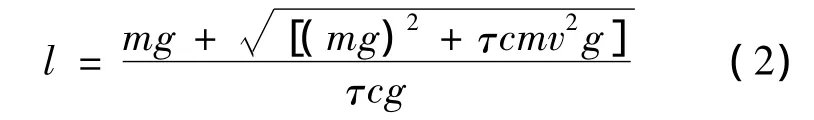
Where，l is the sampling tube penetration depth;m is the mass quality of the sampling vessel;v is the final velocity of corer;g is the gravitational acceleration;c is sampling tube in the circumferential length(cm);τis sediment limit friction coefficient(kg/cm2)．

2．2．Impact factor equation of penetration depth

According to the hydrodynamic theory，once some various factors are considered，the gravity piston corer’s sinking velocity relationship in the water is:

Where，V is corer’s sinking final velocity;V0is corer’s sinking initial velocity;m is the mass quality of corer;g is the gravitational acceleration;ρcis the mass density of corer;ρωis the mass density of seawater;CDis the drag coefficient of seawater to corer;A is the maximum cross-sectional area of a corer’s sinking level and X is the freedom sinking distance of corer．

By the above mentioned analysis，the gravity piston corer will reach the limits of speed after 6 m distance，and the limit speed is equal to the speed when the X→+∞．

Since X is approaching to infinity，the value ofis approaching to zero．Therefore，the following term is approaching to zero as well．

Thus，Eq．(3)could be simplified as:

Plug Eq．(4)into Eq．(2)，one obtaines:

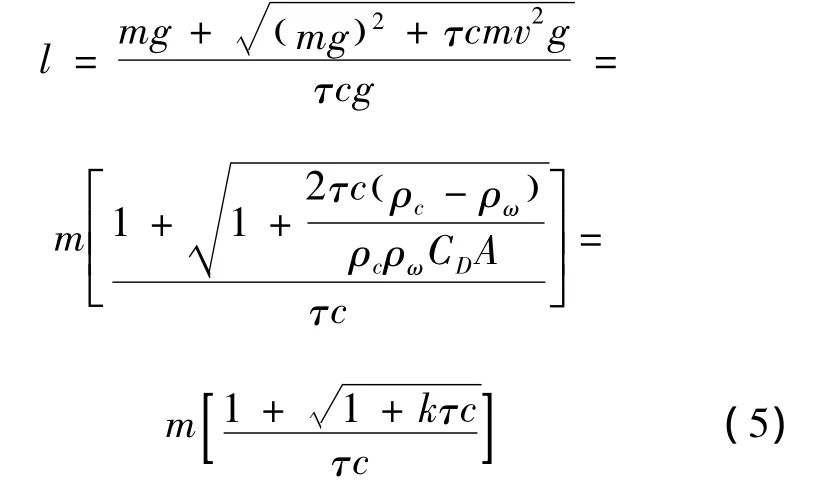
Where，g is a constant;τis related to the nature of sediment(usually measured by experiments，ooze clay)τ =0．05 ～ 0．08(kg/cm2)，sandy ooze clay τ=0．08～0．15(kg/cm2)，clayey sand τ=0．15 ～0．20(kg/cm2)，sand τ=0．20(kg/cm2)．

2．3．Sampling tube’s critical pressure equation in instability

When seabed sediment is penetrated，the model of a sampling tube can be approximately equivalent to a slender rod with the fixed lower end and the free upper end．Based on the strut stability knowledge of material mechanics，it is well known that with the increase of sediment penetration depth，the resistance for the sampling tube will increase［6］．In order to ensure the sampling tube to decline vertically without bending，it becomes essential in the process of penetration to analyze whether the checking sampling tube’s resistance is less than the sampling tube’s instable critical pressure．

According to the Euler’s formula，the critical pressure of the slender rod member can be written as:

Where，μ is the length factor．

The linear empirical formula is often used in engineering to calculate the critical stress，and the relationship between the critical stress and rod flexibility could be expressed as:

Where，a，b are constants related to the material of the lever member．

3．Finite element analysis based on ABAQUS

In order to validate the mathematical theory model，finite element analysis software ABAQUS is adopted to conduct the numerical simulation of penetration process because that ABAQUS has significant advantages in nonlinear analysis as compared with other finite element software［7］．

3．1．ABAQUS finite element analysis modeling

The sampling tube used in this analysis is the PVC inside lining．In order to reduce the disturbance of the sampling tube，the blade of tube is designed to let the soil compaction effect mainly occur in the outer side of the sampling tube during penetration process and it will further reduce the friction between sediment samples and the corer’s inner tube．Therefore，in the finite element modeling process，the contact between the outer wall of the sampling tube and the sediments will be mainly considered，and so does the soil compaction effect occurring in the outer side of sampling tube in the penetration process［8］．The modeling adopts 20 m gravity piston corer，the related parameters are as follows:outer diameter 127 mm，length 20 m，weight 1 800 kg．The elastoplastic model is adopted for soil and the related parameters are:soil width 3．95m，soil length 20 m．In order to constrain all the degrees of freedom at the soil bottom，the degree of soil freedom at the lateral horizontal movement is fixed in the analysis process［9］．During the process that the sampler is penetrated with seabed sediments，the deformation of the sampling tube relative to the deformation of the soil could be neglected［10］．Therefore，the sampling tube could be regarded as a rigid body and it will be controlled to penetrate into the sediment at the depth of 16 m by using displacement penetration method．The surfaceto-surface contact is established between the outer surface of the sampling tube and soil，the friction coefficient is set to be 0．45［11］and the initial penetration speed is 1．26 m/s．

3．2．Analysis of the finite element results

Displacement penetration method is adopted to simulate the penetrating process of corer．Once the numerical simulation is finished，the contours of displacement and stress around the sampling tube after the 20 m gravity piston corer penetrating into seabed sediment at the depth of 16 m could be obtained，as shown in Fig．3．

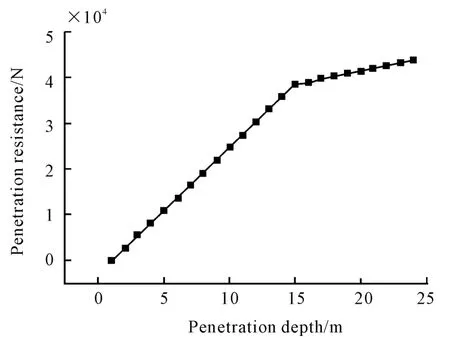
Fig．5 Relationship curve of penetration resistance and depth of penetration

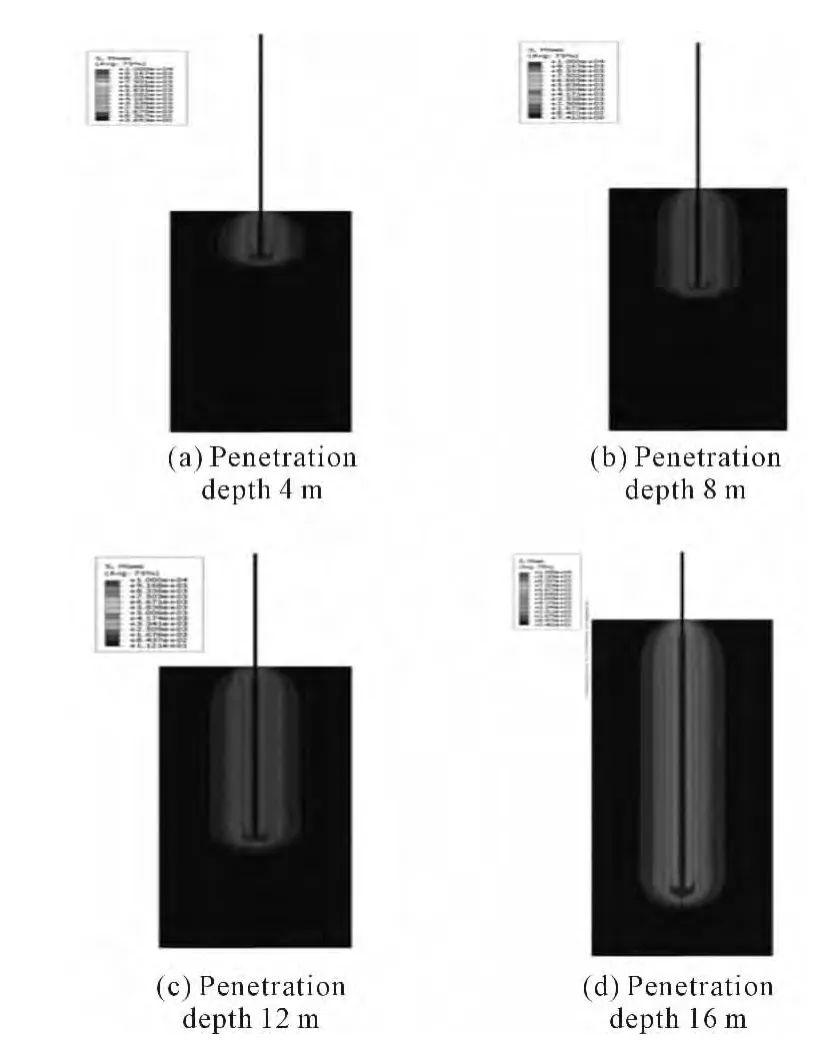
Fig．3 Stress contours in the process of penetration

Based on the data analysis through ABAQUS software，the relationships between instability critical pressure and penetrating depth could be obtained during the corer penetrating process，as shown in Fig．4．In Fig．5，the relationship between penetration resistance and penetration depth is presented;the influence of friction coefficient on the penetration depth is shown in Fig．6;the curve of external acting in the penetration process is shown in Fig．7．

By analyzing the results in Fig．7，when the gravity piston corer penetrates into the sediment at 16m，the consuming energy could be obtained as275 880 J．

According to the penetration depth of Eqs．in 2．2:

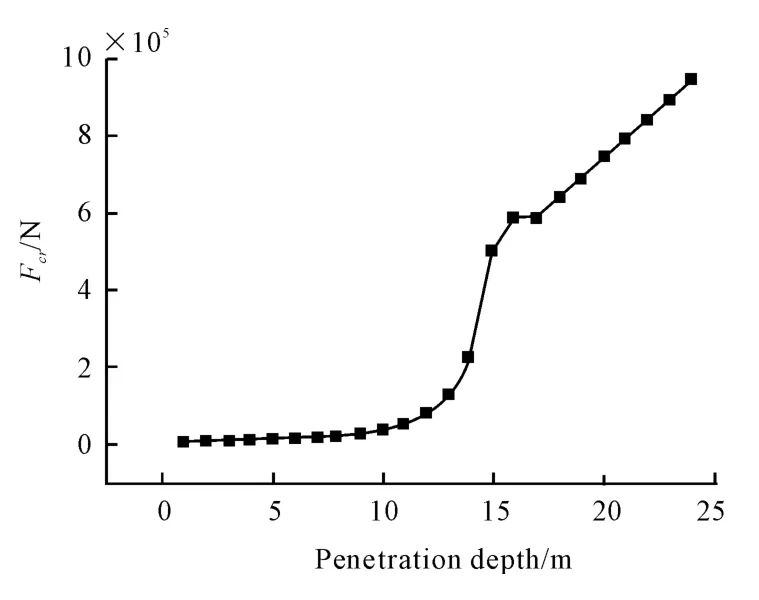
Fig．4 Changes in the relationship between the critical buckling pressure increases with the depth of penetration

Fig．6 Friction coefficient curve of penetration depth

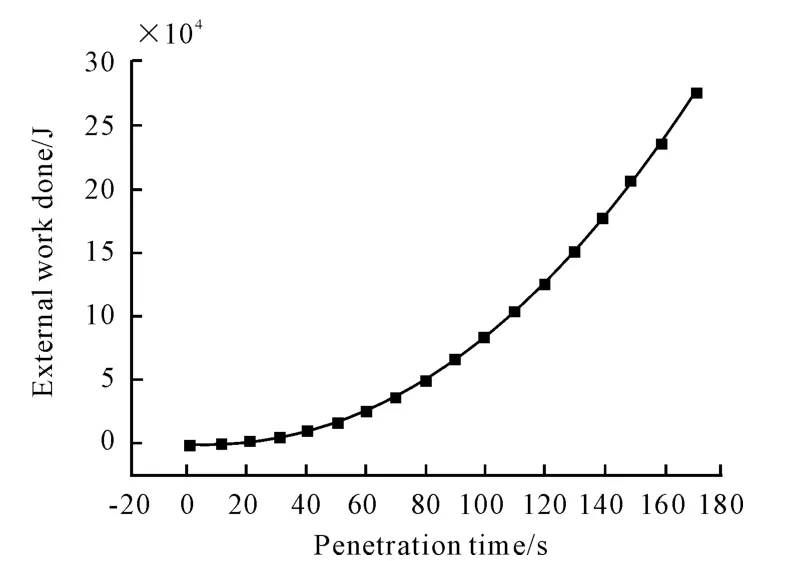
Fig．7 Penetration process of external power curve

Kinetic energy:Ek=1/2mv2=1/2×1800×(1．26)2=1 428．84 J

Gravitational potential energy:Ep=mgh=1 800×9．8 ×16=282 240 J

Through theoretical calculation，the energy of sampler to penetrate into the seabed sediments is mainly supplied by corer’s gravitational potential energy，and the kinetic energy of the corer contributes a small portion during the penetration process due to the low initial penetration rate．In a word，it could be concluded that the results of the theoretical calculation are consist with those of finite element analysis．Therefore，the mathematical theory model is verified．

4．Deep sea sampling test of the gravity piston corer

The parameters of one marine expedition gravity position corer used by the First Institute of Oceanography SOA are as follows:outer diameter is 127 mm and the lead weights counterweight is1 400 kg．Consider weights of the sampling tubes，stripping tube，piston and other components，the weight of the corer is approximately 1800 kg，the maximum cross-sectional diameter D of corer sinking level is 500 mm，and resistance coefficient of seawater to the corer is1．The experimental data is shown in Tab．1．

The calculated penetration depth based on formula(5)and parameters of the experimental gravity piston sampler is shown in Tab．2．

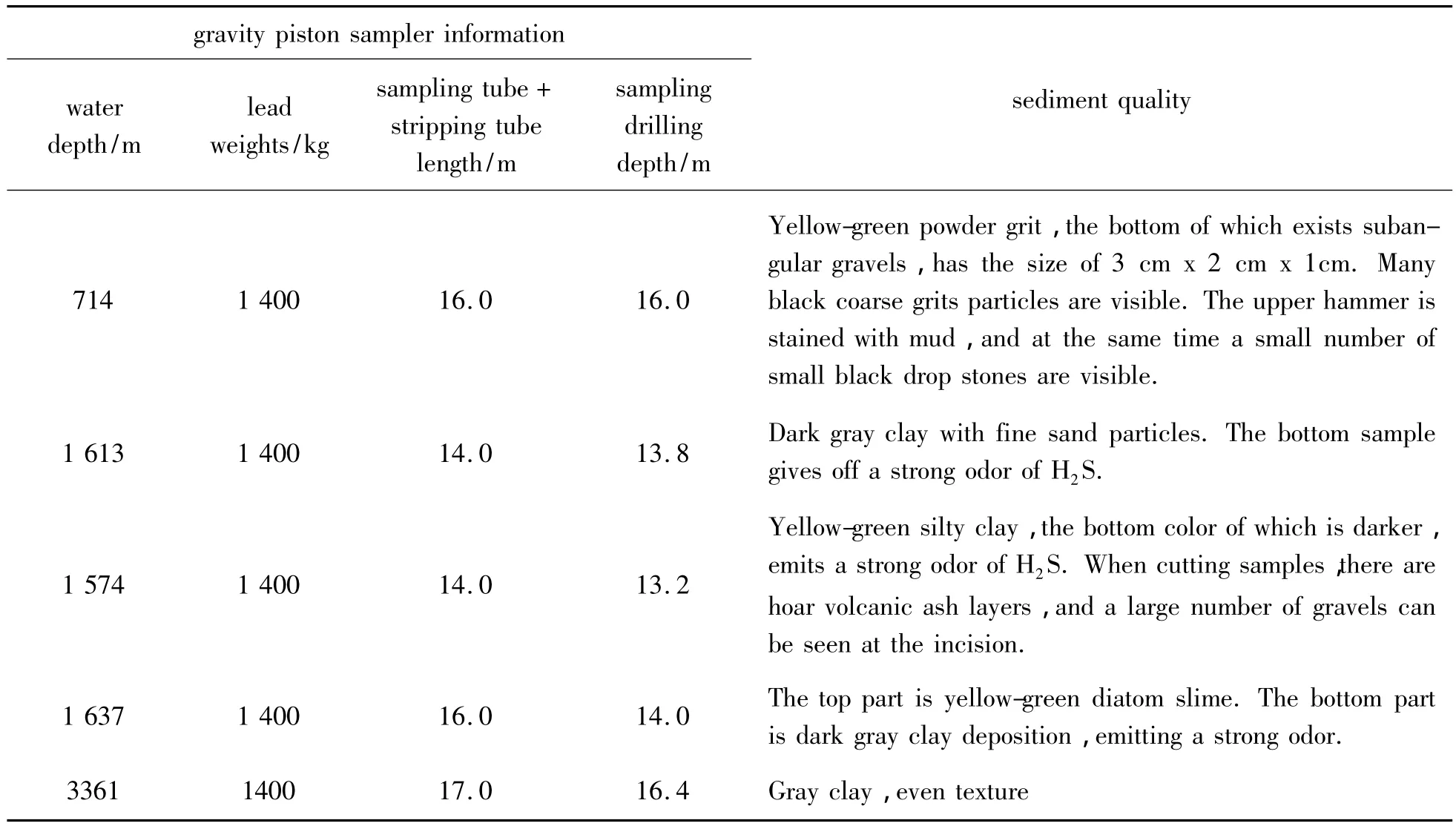
Tab．1 Gravity piston corer’s experimental data of penetration depth

Tab．2 Gravity piston corer’s theoretical calculation data of penetration depth

Through the comparisons between the proposed theoretical results and experimental data，it could be concluded that the differences between them are small，when the limit stress friction coefficient of the seabed sediments is set to be 0．08 ～0．11(kg/cm2)．

5．Conclusions

Through the comprehensive comparisons between theoretical results，numerical simulation and experimental data，it has been confirmed that the theoretical results are consistent with both of numerical simulation data and experimental data．Therefore，the proposed theoretical model has been validated．Since the influential curve of the limit stress friction coefficient of the seafloor sediments on penetration depth of the corer could be obtained through the theoretical model，this model could provide both effective computational method and strong experimental basis for the design of the deep-sea gravity piston sampling．

［1］ YENTaining，BUJiawu，LI Shaojun．Brief Study on the International Present Condition and Develop Tendency of the Technology of Sea Floor Sample Drilling［J］．Geological Science and Technology Information，2000，19(2)：67-70．

［2］ BU Jiawu，YAN Taining，ChANG Zhijun．Introduction to the Status Quo and Operating Principle of Seabed Samplers［J］．Exploration Engineering，2001(2)：44-48．

［3］ RUAN Rui．The Seabed Sampling Technology Explore［J］．Ocean Mapping，2009，1(1)：66-69．

［4］ ZANG Qiyun，HAN Yibing，XU Xiaoshi．Study on the Coring Technique with Gravity Piston Corer［J］．OCEAN TECHNOLOGY，1999，6，18(2)：56-61．

［5］ LI Mingang．Design and Simulation of 40m Gravity Piston Corer［D］．Qingdao：Qingdao Technological University，2012．

［6］ LIU Hongwen．Mechanics of Materials［M］．Beijing：Higher Education Press，2005，12：290-303．

［7］ ZHUANG Zhuo，YOU Xiaochuan，LIAO Jianhui．Finite Element Analysis and Application Based on ABAQUS［M］．Beijing：Tsinghua University Press，2009，1：9-24．

［8］ Chopra M B，Dargush G F．Finite-element analysis of time-dependent large deformation problems［J］．International Journal for Numerical and Analytical Method，1992(16)：101-130．

［9］ Hoyaux B，Ladanyi B．Gravitational stress field around a tunnel in soft ground［J］．Canadian Geotechnical Journal，1970，7(1)：54-61．

［10］ LIU Run，ZHUORuihua，YAN Shuwang．Plug effect on drivability of large—diameter steel pile［J］． THE 0CEAN ENGINEERING，2005，5，23(2)：71-76．

［11］ DING Hongyan，ZHANG Puyang．Visual Simulation of Soil Plug Formation Inside Bucket［J］．PERIODICAL OF OCEAN UNIVERSITY 0F CHINA，2007，37(6)：1034-1038．