基于刚体模态理论的动力总成悬置系统优化设计
胡培龙,曾肇豪
(广州汽车集团股份有限公司汽车工程研究院,广州 511434)
动力总成悬置系统是指动力总成(包括发动机、离合器及变速器等)与车架或车身之间的弹性连接系统。该系统的好坏直接关系到发动机与车体之间的振动传递,影响整车的NVH性能[1]。某款轿车在开发过程中,在怠速工况下,车内方向盘和座椅导轨的振动较大,乘坐舒适性明显不适。本文以该轿车动力总成悬置系统为研究对象,建立动力总成悬置系统模型,计算该模型的刚体模态,发现该模型刚体模态频率分布不合理,模态解耦率较低,因此,对这款轿车的动力总成悬置系统重新进行优化匹配,并在整车状态下进行动力总成悬置系统及方向盘和座椅导轨的振动测试。计算和实验结果表明,合理分配刚体模态频率和提高刚体模态解耦率对整车NVH性能有显著提高[2]。
1 动力总成悬置系统模型
动力总成悬置系统的作用是将动力总成与车身及车架弹性地连接起来[3-4],减小发动机工作时向汽车结构传递的振动,其动力学模型见图1。在动力总成质心O建立固定坐标系O-xyz,各轴的指向分别与汽车坐标系的X、Y、Z轴平行且同向。每个悬置简化为在其3个垂直的弹性主轴方向(u、v和w方向)具有刚度和阻尼的元件,以悬置的3个弹性主轴方向建立悬置坐标系O-uvw。悬置的3个刚度用ku、kv和kw表示[5-6]。动力总成悬置系统的振动微分方程则可以表示为
式中:[M]、[C]和[K]分别为悬置系统的质量矩阵、阻尼矩阵和刚度矩阵,均为6×6的矩阵;{q}、{q˙}、{q¨}和{f(t)}分别为动力总成悬置系统的广义位移向量、广义速度向量、广义加速度向量以及广义激振力,均为1×6的矩阵,{q}={x,y,z,α,β,γ}Τ。
计算模态时,可忽略悬置的阻尼,式(1)可以简化成
根据式(2),可以算出系统的振型矩阵 [φ]=[φ1,φ2,K,φ6]([φi]为第i阶模态振型向量,i=1,2,…,6)以及相应的模态频率ωi。
由此容易得出,系统以第j阶固有频率振动时第k个广义坐标分配到的能量所占系统总能量的百分比[6-7]:
2 动力总成悬置系统计算实例
2.1 动力总成悬置系统参数
该轿车动力总成横置,怠速转速750 r/min,采用支撑式动力总成悬置系统,动力总成通过三个悬置支撑在副车架上,上悬置连杆连接动力总成与车身,主要作用是防止动力总成过大的俯仰运动,如图2所示。
该车型的动力总成的质量为236.6 kg,质心在汽车坐标系的坐标为(-237,21,195)mm,在动力总成质心坐标系 Op-xpypzp中的转动惯量(Ipx、Ipy、Ipz)和惯性积 Ipxy、Ipyz、Ipzx)见表1。以上参数都是通过三线摆的方法测量得到的[9-10]。

表1 动力总成的惯性参数 kg·m2
各悬置在汽车坐标系的安装位置见表2。各悬置的局部坐标系与动力总成质心坐标系平行,即u、v、w分别与x、y、z平行。各悬置的静刚度值见表3,左悬置、后悬置和上悬置连杆的动静比取1.5,右悬置为液阻悬置,其w方向的动静比取2.0。
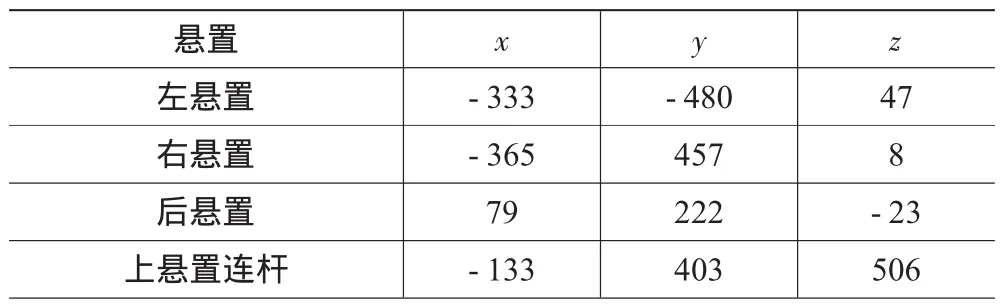
表2 悬置在汽车坐标系的安装位置 mm

表3 悬置的静刚度值
2.2 动力总成悬置系统计算及优化
表4为该轿车动力总成悬置系统模态频率和模态解耦率的计算结果。由计算结果可见,动力总成Pitch模态较高,Fore/Aft和Lateral模态频率间隔太小,各个模态解耦率均太低。从理论上分析,这种不合理的频率分配及较低的解耦率导致悬置系统沿多个自由度方向振动,使悬置系统隔振能力下降,造成汽车怠速时振动偏大。

表4 动力总成悬置系统的固有频率和解耦率(优化前)
对于现已试装的本车来说,由于受整车布置的限制,悬置的位置、安装角度以及悬置的结构都不易改变,因而通过以上方法来改善振动耦合减小振动传递是不容易实现的。考虑到上述实际情况,可在悬置三向静刚度比不变的基础上通过改变悬置主方向的刚度来降低悬置系统的振动。在本优化模型中,选取左悬置、右悬置和后悬置的kw静刚度值以及上悬置连杆的ku静刚度值为设计变量。考虑到悬置的可制造性能及耐久性能,以上四个设计变量的取值范围为100~300 N/mm。
以各个模态频率间隔最大为优化目标,降低Pitch的模态频率,约束各最大的模态频率在2阶怠速频率的倍以下,同时使得Bounce和Pitch的模态解耦率最大。采用序列二次规划算法[11],各个悬置优化后的三向静刚度值如表5所示。

表5 优化后各悬置的三向静刚度
优化后,动力总成悬置系统的刚体模态计算结果如表6所示。优化后由于各个悬置的刚度有所增大,因此,动力总成悬置系统模态频率比优化前的有所增大,但是优化后各个模态频率的间隔变大,分布合理,模态解耦率有所提高。从理论上分析,优化后的动力总成悬置系统的隔振效果会有所改善。

表6 动力总成悬置系统的刚体模态计算结果(优化后)
3 动力总成悬置系统振动测试
为了验证优化前后的动力总成悬置系统的隔振效果,对该轿车进行定置怠速振动测试。测试结果如图3和图4所示。
可以看出,优化后各档位下方向盘和座椅导轨的振动加速度总体上比优化前降低了,尤其是D档降低了59.8%和57.6%。
表7为优化前后怠速工况下,汽车挂D档时,各悬置的振动加速度及隔振量对比。隔振量计算公式如下:
式中:Iso_val为隔振量,dB;aa、ap分别为悬置主动侧、被动侧振动加速度,m/s2。

表7 优化前后D档各悬置的振动加速度及隔振量对比
从表7中数据可得出,优化后各个悬置的隔振量比优化前大,优化后的各悬置被动侧的振动加速度均比优化前的小,在车身结构及转向系统结构不变的情况下,动力总成传递到车内方向盘和座椅导轨的振动加速度会相应减少(见图3和图4)。因此,动力总成悬置系统模态频率的合理分配和模态解耦率的提高可以提高动力总成悬置系统的隔振效果,从而改善车内的NVH性能[12]。
4 结 论
通过对某款轿车动力总成悬置系统动力学模型的计算,找出了怠速工况下车内方向盘和座椅导轨振动较大的原因。在能量解耦理论基础上,通过调整各个悬置的刚度值,对动力总成悬置系统进行了优化设计。结果表明,优化后的动力总成悬置系统的模态频率分配更合理,并且模态解耦率得到了进一步的提高,从而改善了车内的NVH性能[12]。
[1]赵彤航.CA1261汽车发动机悬置系统隔振的研究[D].长春:吉林大学,2003.
[2]王毅,魏道高.发动机总成悬置系统的仿真优化设计[J].汽车科技,2009,(3):37-40.
[3]Shangguan Wen-Bin.Engine Mounts and Powertrain Mounting Systems:a Review[J].International Journal of Vehicle Design,2009,49(4):237-258.
[4]Lewitzke Craig,Lee Ping.Application of Elastomeric Components for Noise and Vibration Isolation in the Automotive Industry[J],SAE Paper 2001,(1):1447.
[5]李忠欣,宋恩栋,叶怀汉,等.混合动力总成多点悬置参数的匹配方法新探[J].客车技术与研究,2012,34(4):7-10.
[6]杨利勇.基于Adams/View的悬置系统工况计算方法[J].公路与汽运,2009,(5)
[7]徐石安.汽车发动机弹性支承隔振的解耦方法[J].汽车工程,1995,17(4):198-204.
[8]上官文斌,蒋学锋.发动机悬置系统的优化设计[J].汽车工程,1992,14(2):103-110.
[9]上官文斌,贺良勇,田子龙,等.汽车动力总成质心与惯性参数测试实验台的开发[J].振动工程学报,2006,23(2):119-125.
[10]徐中明,李晓.动力总成悬置系统改进与试验分析[J].重庆理工大学学报:自然科学版,2012,(1):6-10.
[11]Byrd R H,Nocedal J.Analysis of Reduced Hessian Methods for Constrained Optimization[J].Numerical Programming,1991,49:285-323.
[12]庞剑,谌刚,何华.汽车噪声与振动-理论与应用[M].北京:北京理工大学出版社,2006.

