钻孔灌注桩泥浆流变特性及水力参数研究分析

郑秀华，张新明，于进洋，陈 曦，刘选朋，刘翠娜，梁 楠

(1.中国地质大学(北京)，北京 100083;2.中航勘察设计研究院有限公司，北京 100098)

1 前言

钻孔灌注桩施工地层常是覆盖层较厚或软弱的冲积层，而且很少由单一土质构成，大多数是由粘土、粉土、砂和砾石等互层构成。对于这样的复合地基，一般是不良地质体，最容易坍塌。钻孔灌注桩泥浆主要功能是稳定孔壁、悬浮和携带钻渣(Giu，1980;李月良，1987;荆和平，1990;徐奋强等，2004)。钻孔灌注桩泥浆性能主要包括密度、粘度、静切力、失水量、泥皮质量、含砂量、胶体率和pH值。其中，密度提供液柱压力平衡地层压力，正循环泥浆粘度和切力对于稳定孔壁、悬浮和携带钻渣具有重要意义。

泥浆的流变特性和水力参数在石油钻井和地质勘探中已经有比较深入的研究。与石油钻井和地质勘探相比，钻孔灌注桩具有自身特点，如孔径大，孔深小、要求泥浆成分简单、环保且成本低廉(Zomora et al.，1997;荆和平等，2001;刘睦峰等，2010;占样烈等，2010)。钻孔灌注桩泥浆的流变特性评价和水力参数分析有自己的特点。本文实验研究表明，钻孔灌注桩泥浆流变特性可用宾汉塑性流变模式描述。由于其钻孔灌注桩循环速度低，孔径大，其剪切速率低，用低剪速率下的数据评价其流变参数更科学。

2 流变特性分析

2.1 钻孔灌注桩泥浆流变性能实验研究

钻孔灌注桩泥浆根据所钻地层不同可以采用膨润土配制;也可以用清水钻井，利用地层粘性土自造浆(地层粘土质量不好时需要掺加膨润土);对于复杂地层，需要添加一些处理剂配制优质泥浆(DZ/T 0155－95，1995)。用 ZNN－D6S型六速旋转粘度计，对几种典型钻孔灌注桩泥浆进行了实验，实验数据见表1。

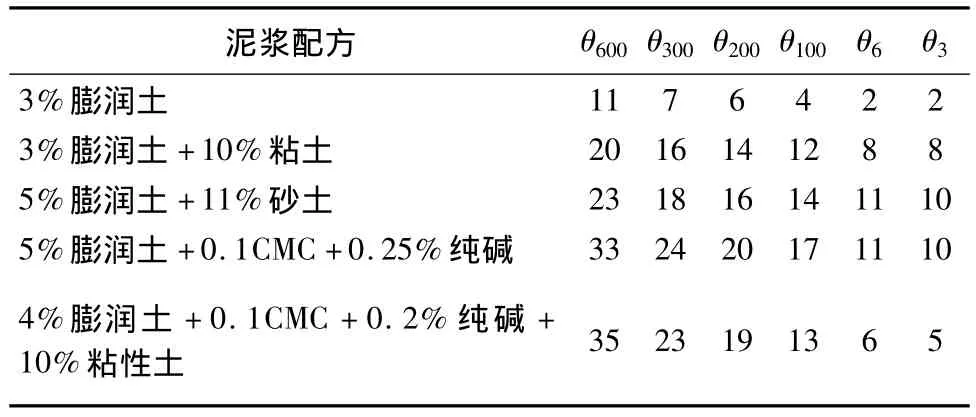
表1 流变性能测试Table 1 Test results of rheological properties of mud with varied components

由公式(1)、(2)和表1数据计算出常用钻孔灌注桩泥浆的剪切应力和剪切速率并绘制流变曲线(见图1)。

式中，τ为剪切应力，Pa;θN为转速为Nr/min时的读数，无量纲。

式中，γ 为剪切速率，s－1;N 为转速，r/min。

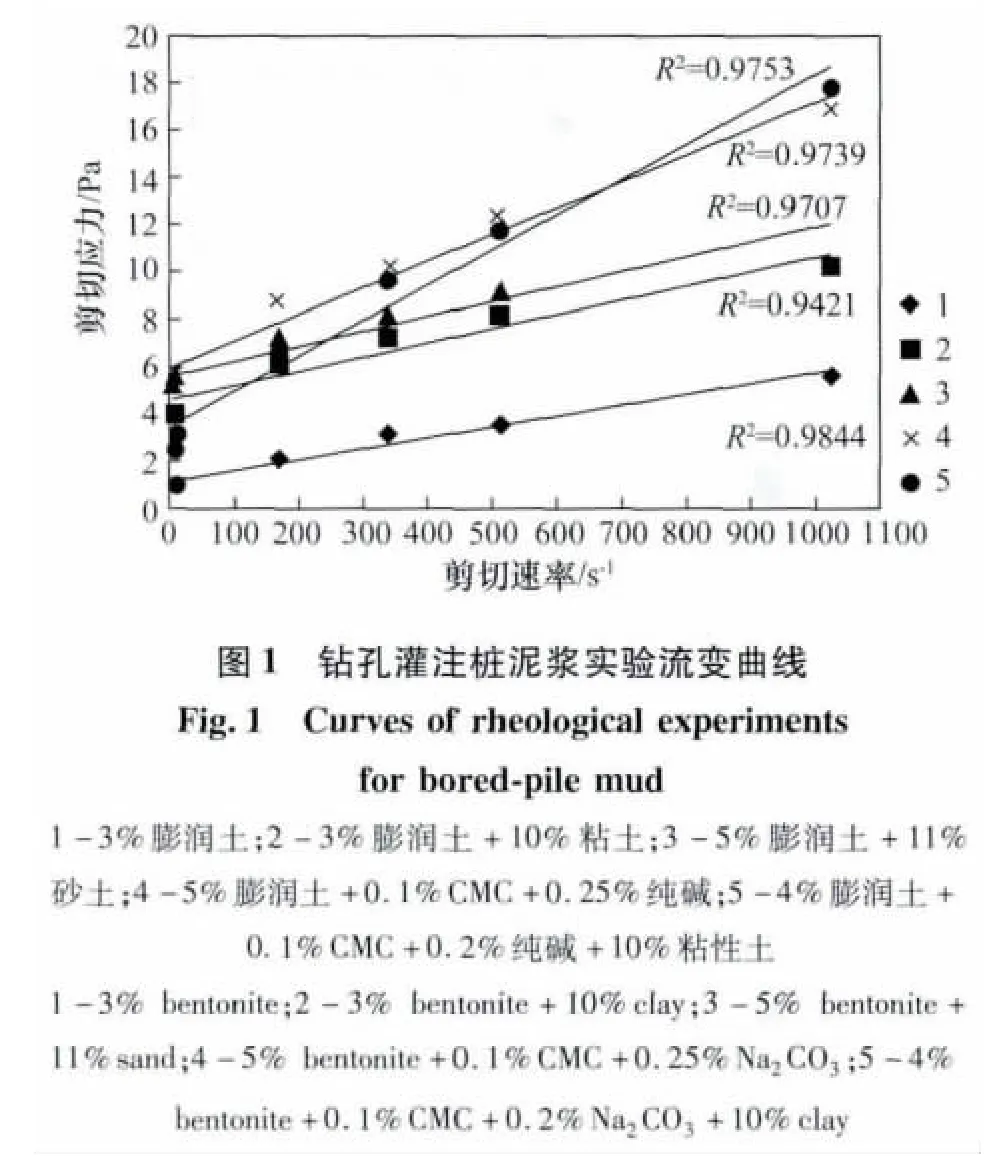
由图1可以看出，决定系数R2均接近1，钻孔灌注桩泥浆的剪切速率与剪切应力呈线性关系，基本满足宾汉流体模式的流变方程τ=τd+μpγ，因此可以判定钻孔灌注桩泥浆为宾汉塑性流体(乌效鸣等，2002;鄢捷年，2006)。

2.2 正循环钻孔灌注桩泥浆流动特性

在施工中常因为泵量不足影响钻进速度，使孔底岩屑增多，回转阻力增大，松散地层也会因泵量过大而冲垮孔壁甚至造成事故。根据有关资料经验(林宗元，1993)，在非固结地层钻进时泥浆上返速度不宜超过0.17m/s;而如稳定地层采用牙轮或钢粒钻进时，泥浆上返速度一般取 0.25～0.5 m/s。由于环空内泥浆上返速度低，其剪切速率大多数在0 ～30s－1范围内(见表2)。

2.3 钻孔灌注桩泥浆流变参数计算分析

钻孔灌注桩泥浆属于宾汉塑性流体，流变参数包括塑性粘度(μp)、动切力(τd)、动塑比、有效粘度(μe)和静切力(τs)。用六速粘度计测试，其流变参数计算如下:

表2 正循环环空内剪切速率Table 2 Share rate in annular space

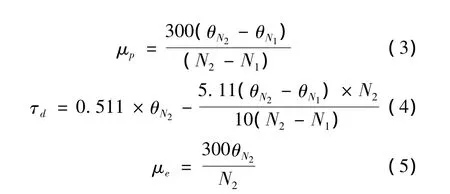
式中，μp为塑性粘度，mPa·s;N1、N2为六速旋转粘度计的转速，r/min;θN1、θN2为转速分别为 N1、N2r/min时的读数，无量纲。τd为动切力，Pa;μe为有效粘度，mPa·s。

在石油钻井和地质勘探泥浆中，N2和N1分别取600r/min和300r/min，计算公式分别为 μp= θ600－ θ300，τd=0.511(2θ300－ θ600)，μe=0.5θ600。由于钻孔灌注桩孔径大，泥浆在循环过程中处于低减速率范围内，需要重新推导计算公式。由公式(3)、(4)和表1实验数据，分别计算各转速段内的塑性粘度和动切力(见表3)，并由公式(5)和表1实验数据，分别计算不同转速对应的有效粘度(见表4)。

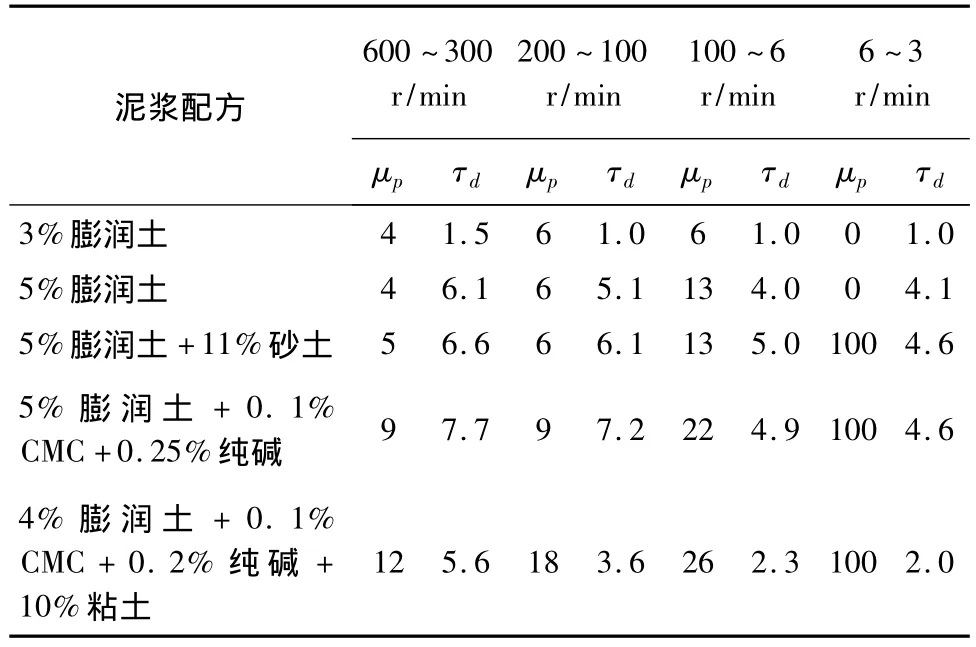
表3 不同转速段的塑性粘度和动切力Table 3 Plastic viscosity and yield values in different rotationspeed ranges

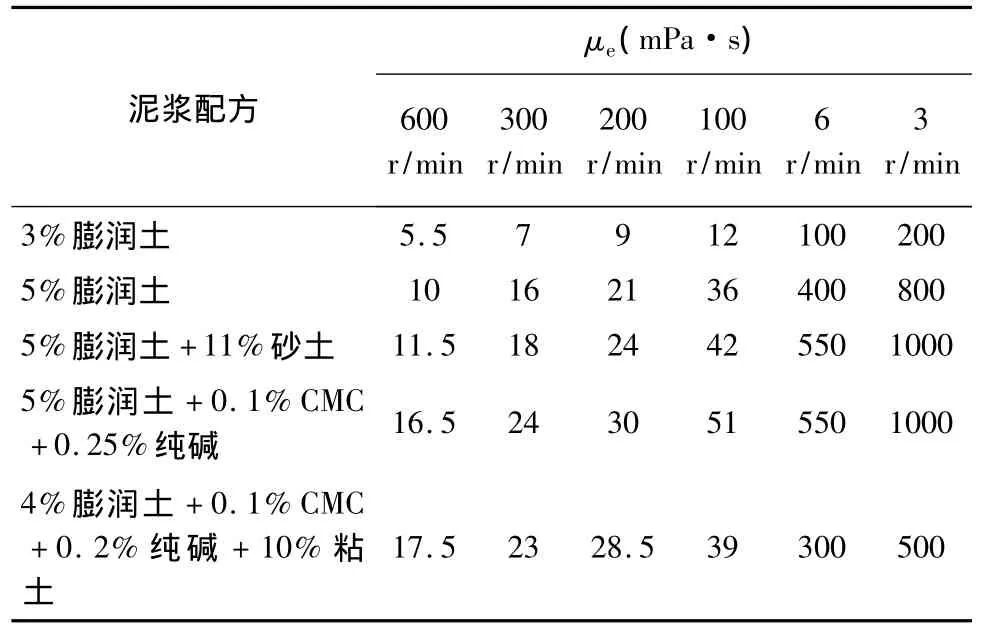
表4 不同转速下的有效粘度Table 4 Effective viscosity at different rotation speeds

由表3、4中数据可以看出，不同的转速段所得到的塑性粘度和动切力是不同的，不同转速对应的有效粘度之间差距很大。钻孔灌注桩桩径大，上返速度低，剪切速率低，因此可采用100～6r/min和6～3r/min两个分段来计算塑性粘度和动切力。但是从表3中6～3r/min分段的计算结果可以看出由于六速粘度计仪器本身的精度问题会出现异常值，因此采用100～6r/min计算塑性粘度和动切力。根据钻孔灌注桩泥浆的低剪切速率范围(0～30s－1)，采用3r/min计算有效粘度。

综上分析，将100r/min和6r/min代入公式(3)、(4)，将3r/min代入公式(5)，推导出塑性粘度、动切力和有效粘度的计算公式如下:

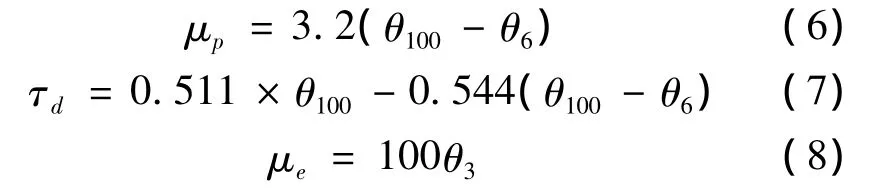
动塑比即宾汉塑性流体动切力和塑性粘度的比值，用来表征泥浆剪切稀释性的强弱。由表2中的计算结果，得到几种典型钻孔灌注桩泥浆的动塑比(见表5)。

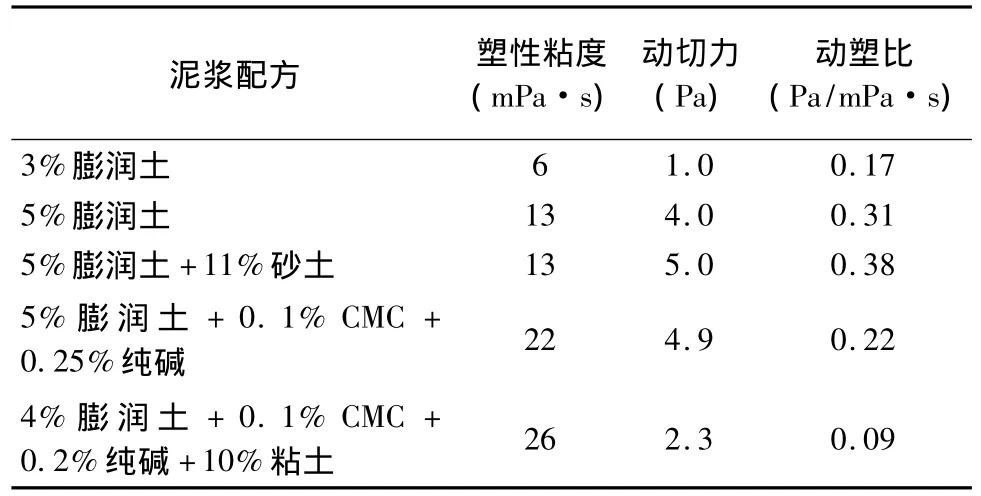
表5 钻孔灌注桩泥浆的动塑比Table 5 Ratios of dynamic stress to plastic viscosity of bored-pile mud

根据现场经验和有关计算，提出动塑比控制在0.36 ～0.48Pa/(mPa·s)是比较适宜的，有利于实现平板型层流，达到稳定井壁和有效携渣的目的。由表3中数据可以看出，几种典型钻孔灌注桩泥浆的动塑比一般小于要求值，可以适当加入黄原胶(XC)提高动塑比。

当泥浆停止循环时，泥浆能迅速形成空间网架结构，将钻渣悬浮起来，或以很慢的速度下沉;而开泵时，泵压又不能上升太高，以防憋漏地层。提供悬浮能力的决定因素是泥浆的静切力和触变性。

假设钻渣颗粒为球形(Concha，2009;刘永建等，1990;周凤石，1982)，根据它们的重力与泥浆对它们的浮力和竖向切力相平衡的关系，可以得到悬浮钻渣所需要的静切力为:

式中，Ds为钻渣或加重剂颗粒的直径，mm;ρs为钻渣的密度，g/cm3;ρm为泥浆的密度，g/cm3;τs为泥浆的静切力，Pa;g为重力加速度，取g=9.8m/s2。

由公式可以看出，有效悬浮钻渣的静切力与钻渣粒径、密度和泥浆密度有关(Chien，1994)。计算不同粒径钻渣在不同泥浆密度中所需静切力见表6。

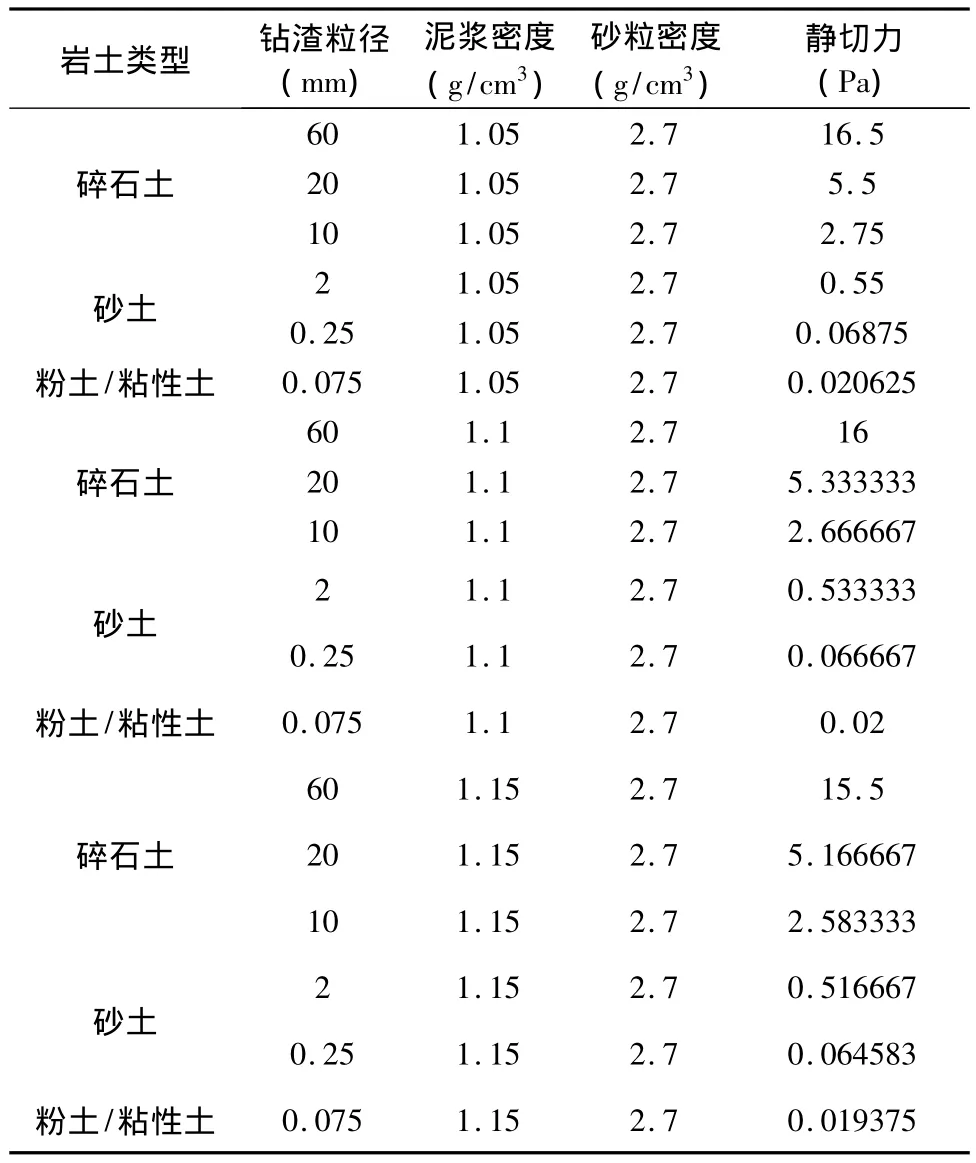
表6 有效悬浮钻渣静切力表Table 6 Static shear stress of effective suspend drilling residual

对于碎石土，钻渣粒径达到60mm时，有效悬浮钻渣静切力＞15Pa;当钻渣粒径为10mm时，有效悬浮钻渣静切力3Pa;对于砂土，其粒径小于2mm，泥浆静切力达到0.5Pa，就可以被泥浆有效悬浮。由六速粘度计测得的实验数据计算出几种典型泥浆的静切力，包括初切力和终切力(见表7)，从表中数据可以看出通过选用不同的泥浆配方一般可以满足悬浮钻渣的要求。

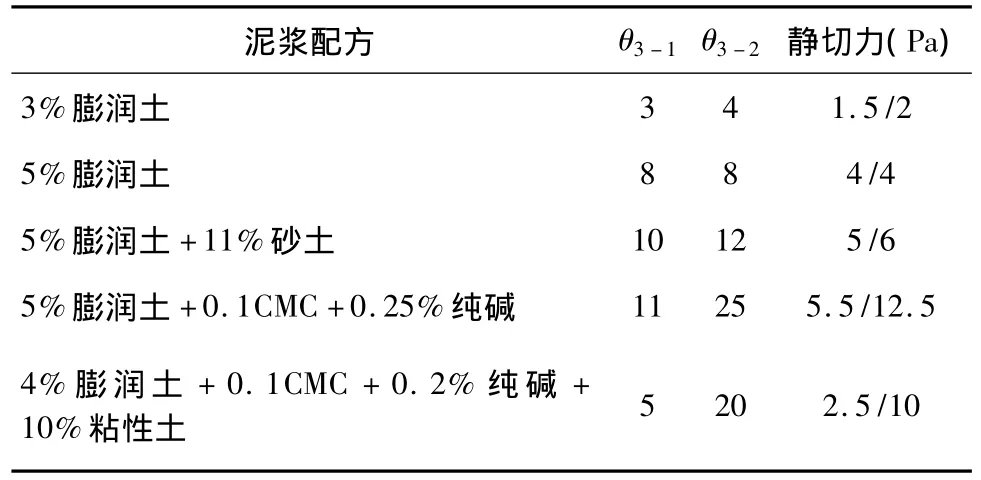
表7 泥浆实验初切力、终切力表Table 7 Initial and final shear stress of mud in tests

3 水力参数分析

钻孔灌注桩泥浆的主要功用之一就是清洗井底并将钻渣携带到地面上来，泥浆的清洗能力除取决于泥浆的流变性能外，还取决于循环系统的水力参数。泥浆流变参数直接用于水力学的有关计算，二者缺一不可。与泥浆携带钻渣密切相关的两个水力学参数是携带比(LC)和雷诺系数(Re)。

3.1 钻孔灌注桩泥浆环空流型分析

紊流上返速度高，携带土渣能力强，但要求泵的排量大(柳宗仁等，2000;査显东，2010)。同时，由于上返速度高对岩土层冲刷容易导致地层失去稳定性，高的上返速度不利于稳定孔/槽壁。因此，钻孔灌注桩泥浆的环空流态应保证为层流。由公式(10)、(11)结合实验数据计算出钻孔灌注桩泥浆在环空中的雷诺系数(见表8)。

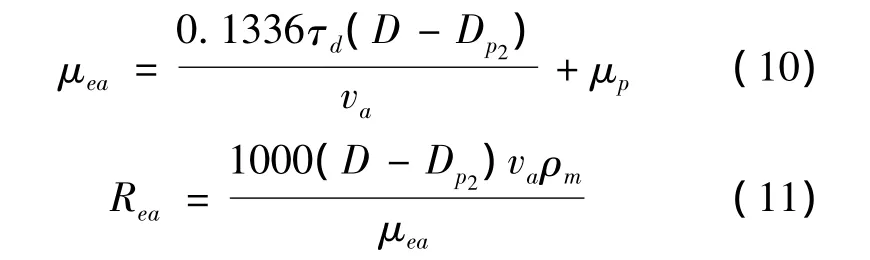
式中，μea为有效粘度，mPa·s;va为上返速度，m/s;D为钻孔直径，mm;Dp2为钻杆外径，mm;ρm为泥浆密度，g/cm3;Rea为环空雷诺系数，无量纲。

从表中数据可以看出，钻孔灌注桩泥浆的环空雷诺系数Re＜2100，属于层流。

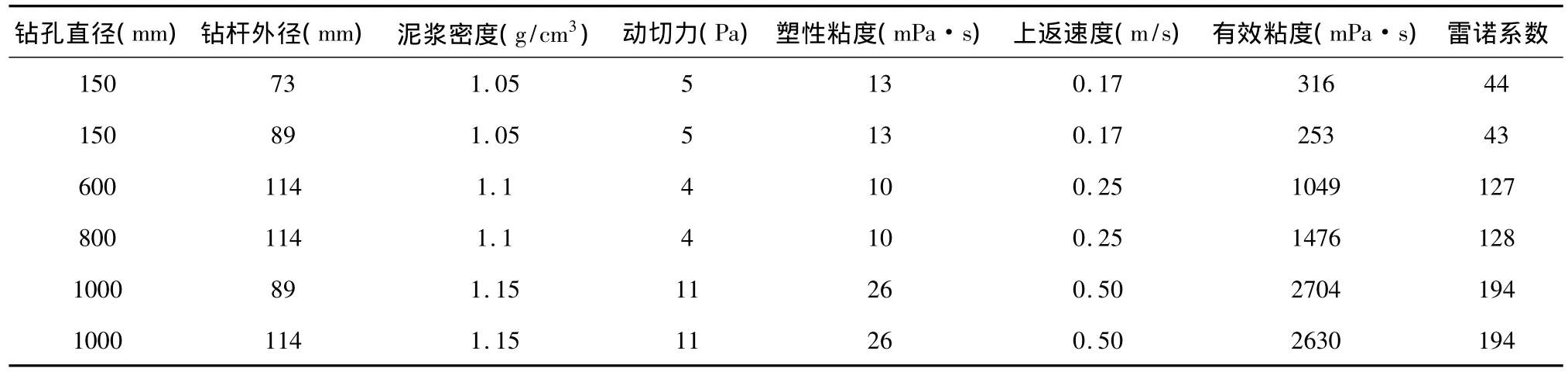
表8 正循环钻孔灌注桩泥浆环空雷诺系数Table 8 Reynolds coefficients of borehole－pile mud in annular space

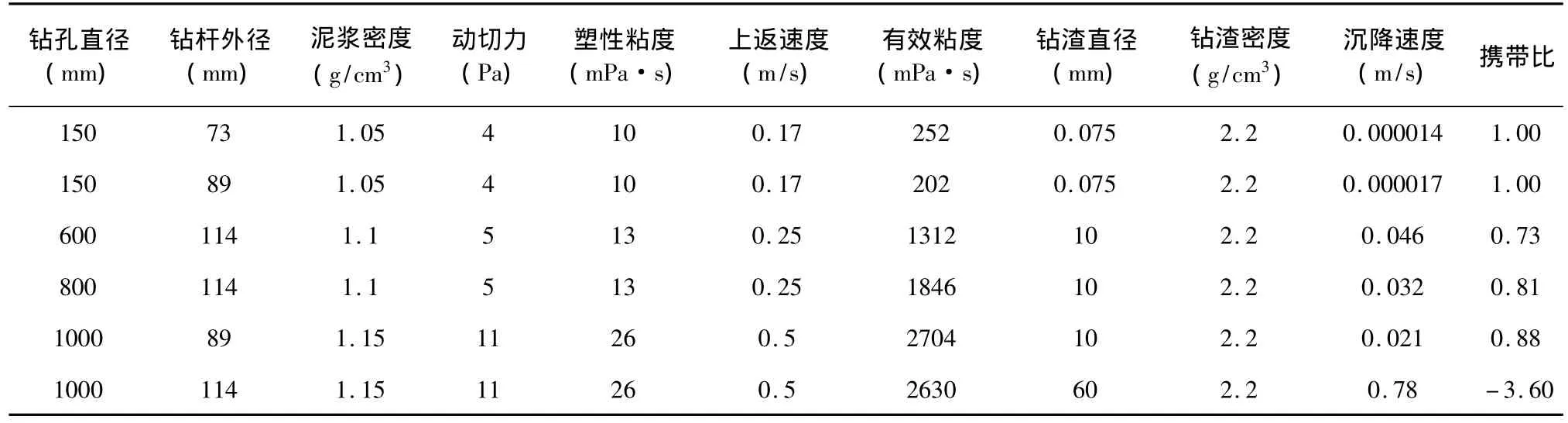
表9 正循环钻孔灌注桩泥浆携渣能力计算Table 9 Carry ability of drilling residual of borehole－pile mud in annular space

3.2 层流携渣原理

钻孔灌注桩桩径大，泥浆上返速度低，环形空间内泥浆处于层流状态。泥浆循环过程中携带钻渣颗粒向上运动，钻渣颗粒由于重力作用向下滑落，钻渣颗粒向上运动的速度取决于泥浆的上返速度与颗粒自身滑落速度之差，即

式中，vp－岩屑的净上升速度，m/s;va－泥浆的上返速度，m/s;vs－钻渣的沉降速度，m/s。

钻渣颗粒的沉降速度与钻渣颗粒的尺寸、钻渣的密度、泥浆密度和泥浆有效粘度有关(方国球，1995;SY5234 －2004，2004)，计算公式如下，

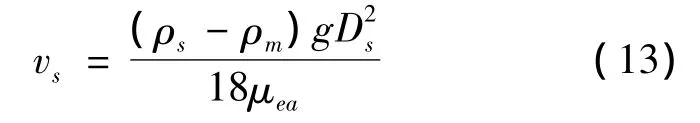
式中，符号物理意义同前。

vp/va为泥浆的携带比，携带比大于等于0.5时认为泥浆能够稳定有效携带钻渣。

从表9数据可以看出，对于稳定地层(如粘土层)，上返速度在0.17m/s时即可满足携渣要求，也可以在泵量允许范围内适当提高返速;对于非固结地层返速在0.25～0.5m/s时一般也可以满足携渣要求，但当钻渣颗粒尺寸特别大时无法靠提高返速将其携带到地面，可以通过重复破碎将少量大块钻渣携带出地面。

4 结论

实验研究表明钻孔灌注桩泥浆基本属于宾汉塑性流体。推导出适合评价钻孔灌注桩泥浆的流变参数计算公式。指出钻孔灌注桩泥浆的层流特性，并对其悬浮和携渣特性进行了定量分析。

Chien S.F.1994.Settling velocity of irregularly shaped particles［R］.SPE Drilling＆ Completion，9(4):281－289

Concha F.2009.Settling velocities of particulate systems［J］.KONA Powder and Particle Journal，27:18 －36

DZ/T 0155－95.1995.Bored-pile construction practice［S］.Beijing:Geological Publishing Press:25－28(in Chinese)

Fang Guo-qiu.1995.An experimental study of free settlement of drilling cuttings in drilling fluid － Drag coefficient and settling velocity［J］.Exploration Engineering，5:41 －43(in Chinese with English abstract)

Giu S A.1980.Applications of slurry walls in civil engineering［J］.Journal of Construction Division，106(6):156－157

Jing He-ping.1990.The cleaning action of foam liquid for rock powder［J］.Geology and Prospecting，12:45－47(in Chinese with English abstract)

Jing He-ping，Jing Ming，Liu Ning-sheng.2001.The alternative of large diameter bored bit and drilling technology in the bounder bed［J］.Geology and Prospecting，37(4):79－80(in Chinese with English abstract)

Li Yue-liang.1987.SM vegetable gum drilling fluid which is used for drilling in cobble stone［J］.Geology and Prospecting，5:69 － 73(in Chinese with English abstract)

Liu Yong-jian，Sun Wei-lin.1990.Settling velocity of spherical drilling cuttings in Herschel-Bulkley fluid［J］.Oil Drilling and Production Engineering，3:15－18(in Chinese)

Lin Zong-yuan.1993.Geotechnical processing manual［M］.Shenyang:Liaoning Science and Technology Press:453－455(in Chinese)

Liu Zong-ren，Wang Zhen-fu.2000.The pumping rate optimization of pumping reverse-circulation under-reamed bored pile［J］.Geology of Shanxi，18(2):68 －71(in Chinese)

Liu Mu-feng，Peng Zhen-bin，Wang Jian-jun，Peng Wen-xiang.2010.Drilling technology of bored-pile in alternating layer of hard and soft rock［J］.Journal of Central South University(Science and Technology)，41(3):1109－1115(in Chinese with English abstract)

SY/T5234－2004.2004.Basic Methods for Optimized Drilling and Applications［S］.Beijing:Petroleum Industry Press:28 － 41(in Chinese)

Wu Xiao-ming，Hu Yu-le，He Bing-xin，Cai Ji-hua.Drilling fluid and geotechnical mud［M］.Wuhan:China University of Geosciences Press:1－105(in Chinese)

Xu Fen-qiang，Wang Xu.2004.Research on stability of hole wall of deep bore hole with mud dado and limit deepness of bore hole［J］.Journal of Lanzhou Jiaotong University(Natural Science)，23(4)，9－12(in Chinese with English abstract)

Yan Jie-nian.2006.Drilling Fluid Technology［M］.Dongying:China U-niversity of Petroleum Press:57－88(in Chinese)

Zhou Feng-shi.1982.Settling velocity calculation and application of drilling cuttings［J］.Oil Drilling and Production Engineering，7:14－29

Zomora M，Bleier R.1997.Prediction of drilling mud rheology using a simplified Herschel-Bulkley model［J］.Journal of Pressure Vessel Technology，99(3)，485－490

Zha Xian-dong.2010.Settling velocity analysis of drilling cuttings［J］.Journal of Suzhou University，25(8):58－59(in Chinese)

Zhan Yang-lie，Xu Li-sheng，Li Yue-liang.2010.Analysis and discussion on the rheology of SM vegetable gum drilling fluid［J］.Geology and Prospecting，46(2):343－347(in Chinese with English abstract)

［附中文参考文献］

方国球.1995.钻井岩粉在钻井液中自由沉降的实验研究－岩粉的沉降阻力系数及沉降速度［J］.探矿工程，5:41－43

DZ/T 0155－95.1995.钻孔灌注桩施工规程［S］.北京:地质出版社:25－28

荆和平.1990.泡沫液对岩屑的携带作用［J］.地质与勘探，12:45－47

荆和平，经 明，刘宁生.2001.卵漂石地层大口径钻头与钻进工艺的选择［J］.地质与勘探，37(4):79－80

李月良.1987.一种用于砂卵石钻进的SM植物胶［J］.地质与勘探，5:69－73

刘永建，孙维林.1990.球形岩屑在赫—巴流体中的沉降速度［J］.石油钻采工艺，3:15－18

林宗元.1993.岩土工程治理手册［M］.沈阳:辽宁科学技术出版社:453－455

柳宗仁，王振福.2000.泵吸反循环灌注桩钻进泵量选择的探讨［J］.陕西地质，18(2):68－71

刘睦峰，彭振斌，王建军，彭文祥.2010.一种软硬互叠岩层钻孔灌注桩钻进技术［J］.中南大学学报(自然科学版)，41(3):1109－1115

SY/T5234－2004.2004.优选参数钻井基本方法及应用［S］.北京:石油工业出版社:28－41

乌效鸣，胡郁乐，贺冰新，蔡记华.2002.钻井液与岩土工程浆液［M］.武汉:中国地质大学出版社:1－105

徐奋强，王 旭.2004.护壁泥浆与孔壁稳定性及极限孔深［J］.兰州交通大学学报(自然科学版)，23(4):9－12

鄢捷年.2006.钻井液工艺学［M］.东营:中国石油大学出版社:57－88

周凤石.1982.岩屑沉降速度的理论计算及其在钻井中的应用［J］.石油钻采工艺，7:14－29

査显东.2010.钻孔灌注桩沉渣分析及处理方法［J］.宿州学院学报，25(8):58－59

占样烈，徐力生，李月良.2010.SM植物胶冲洗液的流变性分析与探讨［J］.地质与勘探，46(2):343－347