基于移滞模型的河道和流域汇流定量分析

杨 鹏，周 波

（海河水利委员会水文局，天津 300170）

1 前言

目前，国内所采用的水文模型中，一部分是从国外引进的，如美国的萨克拉门托模型、斯坦福模型、日本的水箱模型等，这些水文模型参数较多，对资料条件要求较高，应用复杂，不适合海河流域的实际情况。国内较为完善的新安江模型，主要适用于南方湿润地区，不能完全解决海河流域的汇流计算问题。

本着从实际需要出发，笔者采用移滞汇流模型计算流域汇流，该模型弹性较大，适用性较强，既能反映洪流汇流的调蓄和滞后作用，同时也能反映区间入流和汇流过程中的入渗损失等复杂问题。将其应用于海河流域南系的流域汇流计算中，取得了较理想的成果。

2 模型的基本概念

洪流汇流的动力学特征主要反映在河段的蓄泄关系上，这种关系反映以下特征：洪流水体是一种物体，它和其他任何物体一样，在运动过程中具有物理传播的属性，一定的运动位移必然与相应的滞后时间相联系。同时，洪流水体也是流体，它与刚体位移不同，除传播位移作用外，还有调蓄滞后作用。移滞汇流模型则很好地体现了上述两种作用，该模型既可以用于流域汇流，又可以用于河道汇流，是一个弹性大、适用性广的模型。以河道汇流为例，推求其数学表达式。

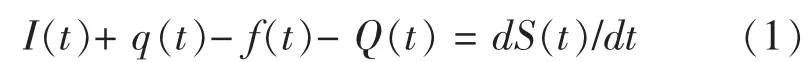
单元河段的水量平衡方程为：式中：I（t）、Q（t）分别为单元河段的入流、出流；q（t）为区间入流；f（t）为河道入渗；S（t）为河槽调蓄。

令：

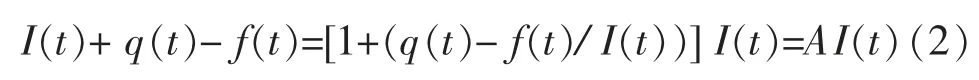
式中：A为河道入渗与区间入流的综合影响系数。

将式（2）代入式（1）得：

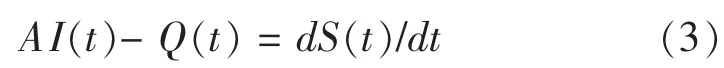
若以线性渠道模拟洪流的传播位移作用，以线性水库模拟洪流的调蓄滞后作用，则单元河段的蓄泄方程为：

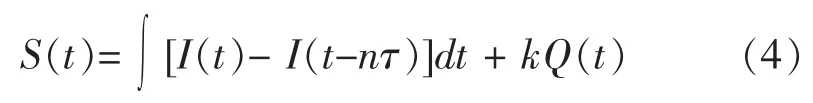
式中：τ、k分别为单元河段的洪水传播位移历时和调蓄滞后历时。

设各单元河段的τ、k值均相等，取上一河段的出流为下一河段的入流，逐次代换，连续演算，则n个河段的入流、出流关系式为一n阶线性常微分方程。

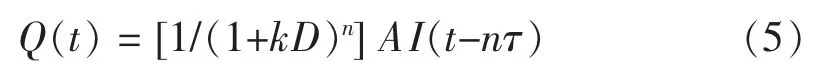
式中：n为单元河段数；D为微分算子。

设A为常数，由卷积公式得：

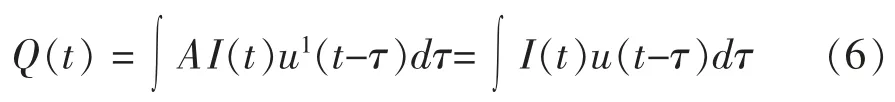
因此，u（t-τ）=A u1（t1-τ），能反映河道汇流入渗和区间入流的综合影响。

对式（5）进行拉普拉斯变换，根据海维赛德平移定理，可得到三参数瞬时河道移滞模型。

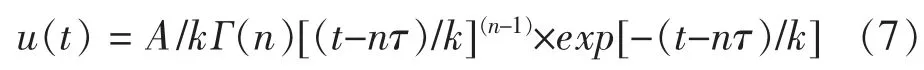
式中：Г（）为伽玛函数。

当n=1时，式（7）就变为迈耶（Meyer）的滞后演算法。当τ=0时，式（7）就变为加里宁—米留柯夫瞬时河道汇流模型，移滞河道汇流模型的适应性显然优于上述模型。

通过S曲线可将瞬时河道移滞模型转化为时段河道移滞模型。

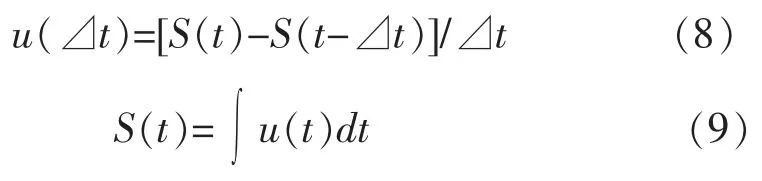
移滞河道汇流模型同样可以用于流域汇流，其入流为时段净雨。也可根据降雨直接进行流域汇流计算，但需在系数A前乘以径流系数r。

移滞汇流模型中的三参数（n，τ，k）原则上可用入流、出流的一、二阶原点矩和二、三阶中心矩与移滞汇流模型三参数间的矩式关系确定。但由于高阶矩式的计算误差常因净雨过程的推求和基流分割的任意性而难以控制，所以利用入、出流对应的水文关系式代替部分高阶矩式可以减少计算误差。

当入流洪峰移滞历时tp和起涨点的传播位移历时nτ均能确定时，则只需借助一阶矩式推求其他参数。式中：m1为移滞模型的一阶原点矩，即入流过程与出流过程重心间的时距；nk为入流的调蓄滞后历时；tp为入流洪峰与出流洪峰间的时距。已知nτ、tp、m1，由式（10）、（11）即可确定n、τ、k三参数的值。

3 汇流模型检验

对于各区间流域及河道，用流域面平均净雨总量（p）或上游断面洪峰值（Qm）与m1、nτ或nk及tp画关系曲线，p或Qm与m1、nτ或nk及tp呈反比关系，均为一条单一曲线。这表明大洪水汇流时间短、调蓄滞后作用小，小洪水汇流时间长、调蓄滞后作用大。实际模拟计算时，只要算出净雨总量或用上游断面的洪峰就可查出m1、nτ或nk及tp值，用式（10）和（11）即可算出n、τ、k值。

为检验汇流模型，流域汇流选择了历史上曾多次发生大洪水且资料较为完整的海河流域大清河北支张坊（控制面积4 810 km2）、东茨村（控制面积1 480 km2）、北河店（控制面积1 530 km2）进行检验计算，河道汇流选择了大清河张坊至新盖房河段（河长83.7 km）进行检验计算。资料采用20世纪50年代以后的几场大洪水，尽可能利用现有资料，以提高代表性。其流域汇流与河道汇流的计算均采用移滞汇流模型，流域汇流的入流为面平均净雨，出流为控制断面出流；河道汇流的入流为河道上断面入流，出流为河道下断面出流，两者计算方法一样。

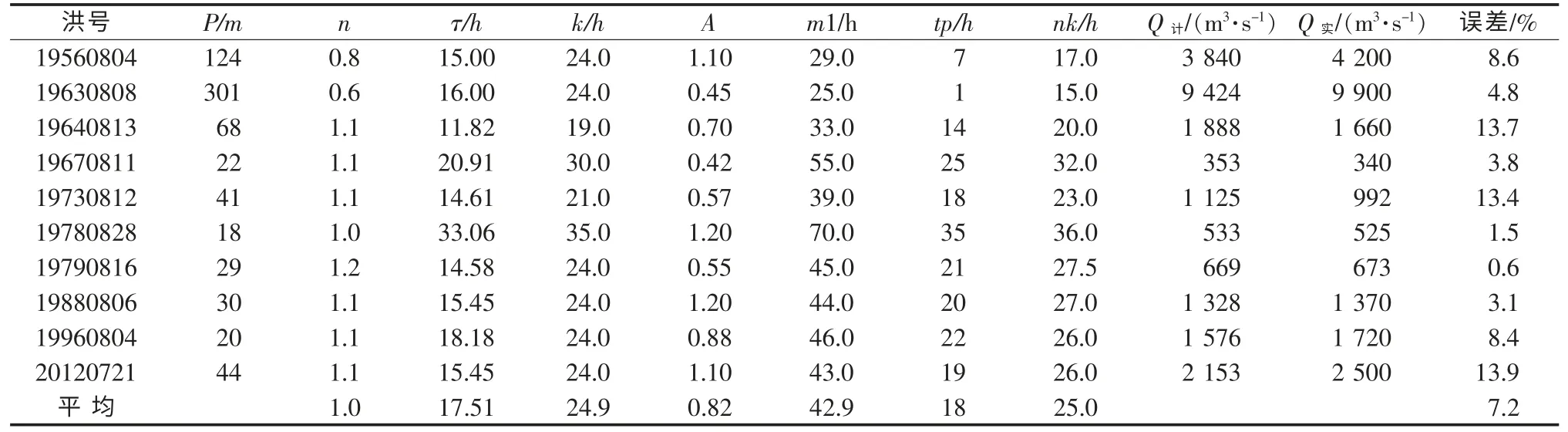
表1 张坊以上流域汇流计算成果（综合参数后）

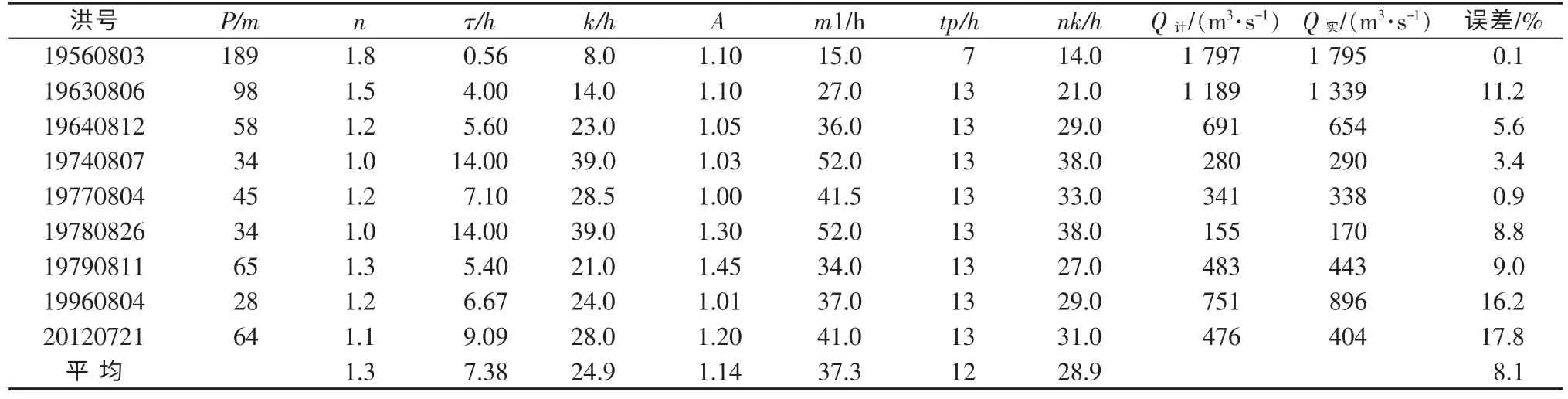
表2 张坊—东茨村区间流域汇流计算成果（综合参数后）

流域汇流模拟结果如下：张坊站10场洪水模拟洪峰相对误差最大为13.9%，平均误差7.2%（详见表1）；东茨村站9场洪水模拟洪峰相对误差最大为17.8%，平均误差8.1%（详见表2）；北河店站7场洪水模拟洪峰相对误差最大为22%，平均误差13.7%，有2场洪水误差超过20%（详见表3）；新盖房站7场洪水河道演算洪峰相对误差最大为12.3%，平均误差4%，有6场洪水误差小于10%（详见表4）。

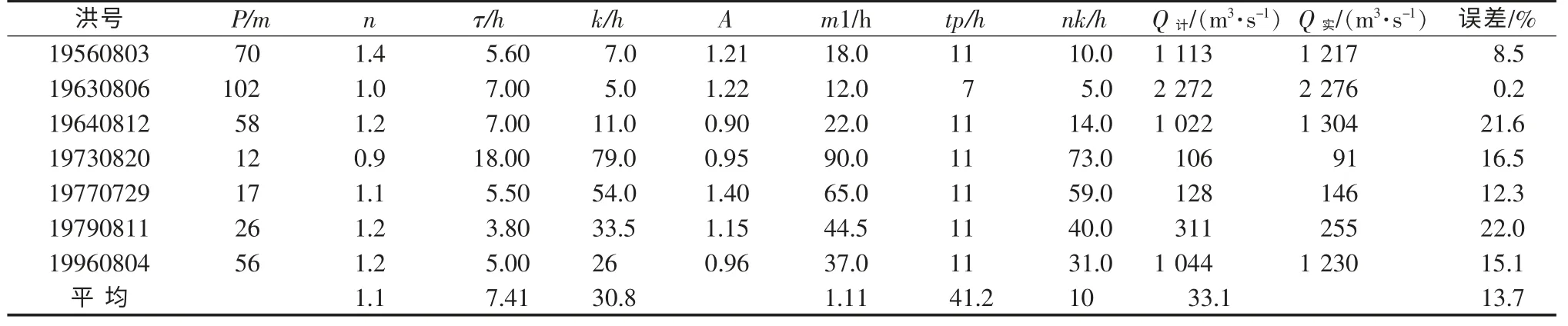
表3 张坊-北河店区间流域汇流计算成果（综合参数后）

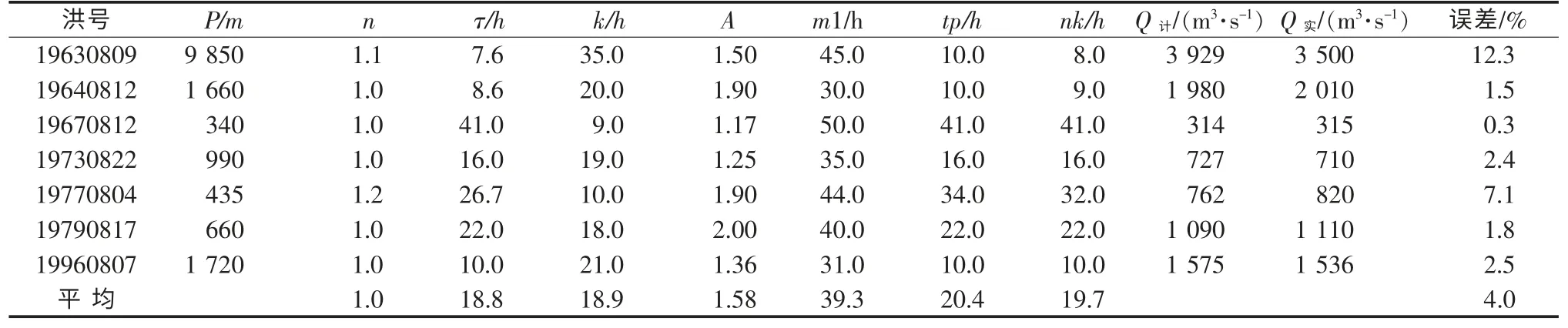
表4 张坊-新盖房河道汇流计算成果（综合参数后）

4 结果分析

对于有区间入流的流域，由于下游出口断面流量包括区间降雨产流和上游河道入流两部分，在分离区间降雨产流产生的流量过程时，采用下游出口断面流量过程减去上游洪水演算到下游断面的流量过程，其产生的误差导致p～tp关系紊乱，无法定线，因此采用了降雨分级法确定tp。在Qm～m1相关线中，m1是以上、下游河段的洪水最快传播时间为渐近的。

移滞汇流模型对洪水的涨水段和洪峰有较高的模拟精度，尤其对于双峰和多峰型降雨反映较敏感，对于复式峰能较好地模拟。该模型适用范围较广，在海河流域大清河北支的洪峰模拟计算中效果较好。总之，移滞汇流模型只要合理选择汇流参数，其洪峰模拟精度即能满足防汛要求。