1000MW超超临界汽轮机高压外缸蠕变强度的分析

蒋浦宁

（1.上海交通大学 机械与动力工程学院，上海 200240；2.上海电气电站设备有限公司 汽轮机厂，上海 200240）

目前，我国1000MW超超临界机组的进汽参数已经达到了27MPa／600℃，因此对汽轮机高温、高压外缸进行科学合理的高温力学性能考核评价是决定其设计成功的关键.在机组运行中，高温、高压外缸承受着巨大的蒸汽内压并长期工作在高温环境下，高温和高负荷导致部件蠕变效应非常明显，因此在其结构强度考核分析中必须予以重视［1-2］.

在1000MW超超临界机组高压外缸的蠕变计算中，笔者引入了Norton－Bailey材料蠕变本构方程，解决了材料在高温下应力与应变非线性化的力学模型问题［3-4］，并使用 Cocks－Ashby（以下简称CA）多轴韧度系数对高压外缸的高温蠕变等效应变进行了计算，实现了将材料的高温单轴试验力学性能数据在多轴复杂应力条件下的工程应用［5-6］.

本文研究包括对汽缸轴对称二维模型的温度场、应力场和CA蠕变等效应变分布进行计算，找出结构设计中不合理区域，对汽轮机高压外缸提出结构设计改进方案，然后对汽缸全三维模型进行计算，并在轴对称二维计算结果的基础上，结合全三维Mises等效应变和CA多轴韧度系数计算结果找出最大CA蠕变等效应变位置并对汽缸蠕变应变进行考核评价.

1 高温力学的理论基础

1.1 高温蠕变的本构模型

蠕变是一种在高温状态持久应力作用下与时间有关的塑性变形过程行为，目前工程中广泛使用较为简单的数学表达式——幂率模型来描述蠕变随时间的变化过程.在计算中，笔者采用Norton－Bailey方程进行蠕变本构特征模拟.

1.2 CA系数

通常，材料蠕变断裂应力数据是在高温固定载荷试验条件下获得的.但在工程实际中，当构件发生蠕变时，其内部应力随时间发生变化，高的工作应力会随着时间的延长而逐渐降低.从表面上看，似乎蠕变时间越长，最高工作应力越小，材料则会变得更加安全.显然，这个结论是完全错误的.相比之下，采用应变的积累能够比较真实地反映材料高温载荷条件下的强度特征状态，因此在对高温部件进行蠕变分析或考核时，推荐使用应变考核来取代传统的应力考核方式［7］.

根据传统塑性理论以及Mises屈服准则，采用有限元计算中使用的式（1）就能得到蠕变后的Mises应力.

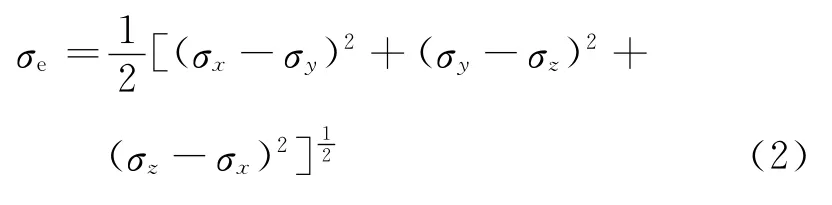
蠕变后的Mises等效应变为

式中：σx、σy、σz分别为x、y和z 3个坐标方向的应力；εx、εy、εz分别为x、y和z 3个坐标方向的应变.

传统概念上认为多轴应力下有效蠕变速率和等效应力的关系与单轴应力下蠕变速率和应力的关系是一致的，因此可以通过有限元计算得到的有效蠕变应变来考核高温蠕变多轴应力状态下的安全性，但是这一方法是建立在理想弹塑性模型基础上的，如果将其直接应用在超超临界汽缸部件结构高温强度评价上则不尽合理，因此只可以作为辅助分析手段，但不可推荐作为最终评价依据［8］.

由于电厂高温部件的失效机理大多受到孔洞长大机制约束，因此只有基于孔洞长大理论的模型才能比较准确地描述汽轮机部件高温条件下复杂应力对材料韧性的影响［8］.在计算中，笔者主要引入了CA模型.CA模型的最大贡献在于解决了将单轴数据推向多轴状态的问题，它以孔洞的受约束长大机理为理论基础，并引入含球形孔的理想圆柱体模型和假设条件而得到一组微分方程，用来转化材料在单轴和多轴应力状态下的蠕变断裂韧性［9-10］.通过求解和拟合得到多轴应力与单轴应力下蠕变失效应变的关联式

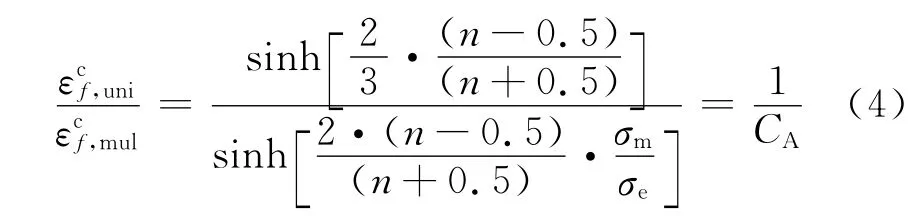
在计算中，只要取单向最大主应变ε1，在式（3）中将其乘以CA就可以获得该点的CA多轴蠕变等效应变εeq，ca.从理论上讲，根据此计算结果来判断多轴蠕变应变强度是偏安全的［11］.

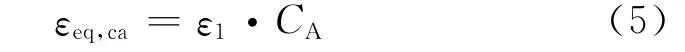
美国的高温压力容器规范ASME BPVC－III（American Society of Mechanical Engineers，Boiler and Pressure Vessel Code，Section III）、英国的高温结构完整性评定规范R5（Assessment Procedure R5）等国外规范都推荐使用考虑多轴效应后的蠕变应变值作为高温应变强度考核标准［12-13］，结合以往工程经验，笔者推荐以小于2%作为高压外缸多轴CA 蠕变等效应变许用值［14-16］.

2 汽缸轴对称二维模型的蠕变考核计算

2.1 轴对称二维模型的结构与边界条件

先将1000MW超超临界汽轮机高压外缸实际结构简化为轴对称二维模型，然后对其进行计算和分析.图1为高压外缸的轴对称二维模型.图1中的二维模型包括6个分段：12CrMoV铸钢后轴封外侧段（1），12CrMoV 铸钢后轴封内侧段（2），1CrMoV铸钢外缸排汽段（3），10CrMoWVNbN铸钢外缸进汽段（4），12CrMoV铸钢前轴封内侧段 （5）和12CrMoV铸钢前轴封外侧段（6）.另外，根据汽缸实际结构，在外缸进汽段（4）内壁装有U型密封环和I型密封环，将其分隔成不同压力的区域：高压第1级回热抽汽腔室、内外缸夹层压力平衡腔室和转子平衡活塞压力平衡腔室，分别用于回热抽汽、降低高压内缸内外压差和平衡高压转子轴向推力.

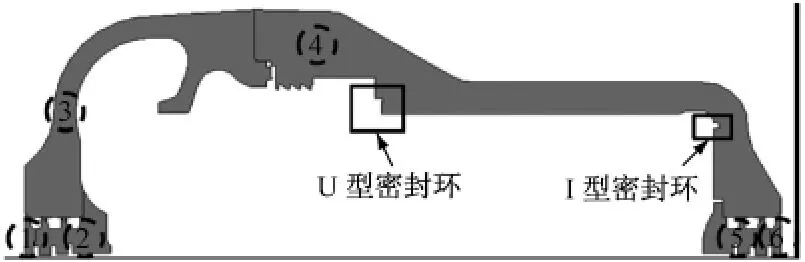
图1 高压外缸的轴对称二维模型Fig.1 2Daxisymmetric model of the HP outer casing

在计算中，首先采用UG建模，然后将其导入Abaqus软件中进行网格绘制.根据汽缸的几何特征，采用轴对称二维坐标建模.有限元几何模型的离散采用四节点CAX8RT单元，计算域单元总数为55117个.计算边界条件分为热学边界和力学边界两类.高压外缸内外壁的传热和载荷边界条件根据汽缸在汽轮机阀门全开（VWO）工况下各位置的温度、压力和传热系数进行选取.

2.2 轴对称二维模型的温度场与应力场

图2给出了汽缸及其附属部件在满负荷VWO工况下的温度场分布.

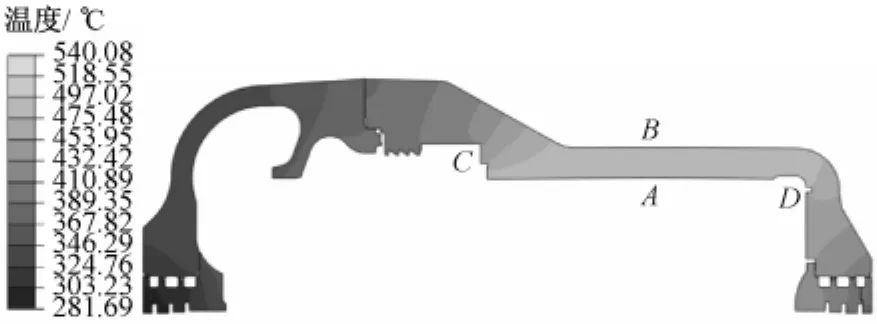
图2 VWO工况下的温度分布Fig.2 Temperature distribution under VWO condition

从图2可以看出，温度最低部位在后轴封段，最低温度为281.7℃.相对后轴封段（1）和（2），前轴封段（5）和（6）与高温平衡活塞压力平衡腔室接触，那里的蒸汽源自高压进汽的漏汽，相对蒸汽温度水平较高，达到420～440℃.外缸排汽段（3）缸壁处于高压缸第1级回热抽汽与高压排汽位置，整体温度在350～420℃.相比之下，外缸进汽段（4）的缸壁温度达到450～540℃，是整个高压外缸分析系统中温度最高的部分，同时也是本文汽缸蠕变强度分析的主要对象.

从图2还可以看出，高压外缸进汽段（4）的温度分布呈现出先沿轴向中间高，然后向两侧逐渐下降的趋势，这是因为进汽段（4）中的2个密封环将其内腔室分隔为3段，腔室间的温差形成较大的部件金属温度梯度.因此在整个计算中，选取工作温度最高区域的内壁A点和外壁B点以及2个密封环所在的温度梯度最大区域C点和D点作为重点蠕变强度考核位置.

对汽缸进行了20万h蠕变计算，得到汽缸20万h蠕变应力比和CA蠕变等效应变.图3给出了高压外缸轴对称二维模型20万h后的蠕变应力比.从图3可知，蠕变应力比最大位置为C点，其比值为0.7793，主要由于此处结构为直角，应力集中显著，相对其他部位，蠕变应力比较大.

图3 高压外缸轴对称二维模型20万h后的蠕变应力比Fig.3 Creep stress ratio based on 2Daxisymmetric model after 2×105 h

图4为C点Mises应力随时间变化的曲线.从图4可知，在蠕变作用下，C点初始工作应力为302 MPa，在发生蠕变效应后，高应力区域的应力值随着时间逐渐减小，起初C点应力下降剧烈，但由蠕变应变本构方程式（1）可推出，应力会影响蠕变速率，而蠕变同时反过来又会影响应力，在二者相互作用下，此应力下降由强变弱并逐渐趋于平缓.该曲线说明，在高应力位置的工作应力从蠕变一开始就大幅下降到长期蠕变后的应力水平，因此笔者再次强调：对经过蠕变后的应力进行长期蠕变强度考核分析不一定正确合理［7］.

2.3 轴对称二维模型CA等效蠕变应变场

利用式（2）和式（3）计算进汽段（4）的CA 蠕变等效应变.图5给出了高压外缸轴对称二维模型20万h后的CA蠕变等效应变计算结果.从图5可以看出，高压外缸进汽段中部的CA蠕变等效应变值较大，主要原因是该处的蒸汽温度最高.而高压外缸两端部件的蒸汽温度较低，因此蠕变应变值较小，其量级为10－3.

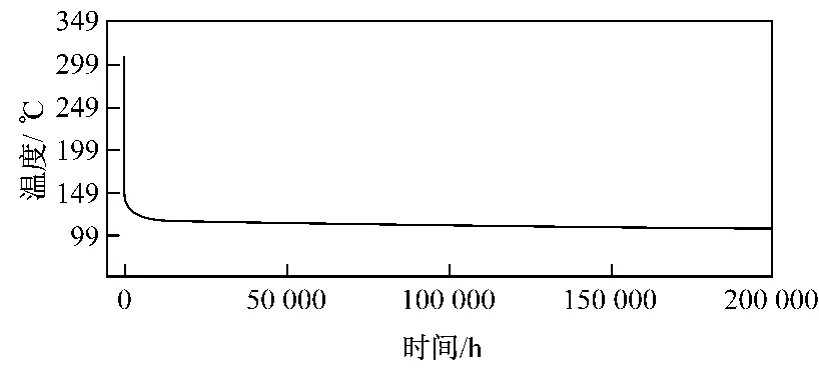
图4 C点Mises应力随时间变化的曲线Fig.4 Mises stress at point Cvs.time

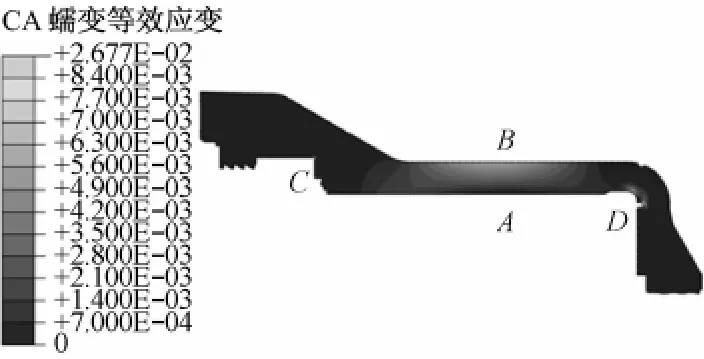
图5 轴对称二维模型20万h后的CA蠕变等效应变Fig.5 CA equivalent creep strain based on 2D axisymmetric model after 2×105 h

高压外缸各点的CA蠕变等效应变计算结果见表1.从表1可以看出，A、B、D点20万h后的蠕变应力比均小于1，而20万h后的CA蠕变等效应变均小于2%.但是，在对C点的计算结果中发现，虽然蠕变应力比也小于1且不是应力最大的点，但是20万h后的CA蠕变等效应变超过了工程许用值2%.这更清楚地说明，在高温强度考核中采用应力考核会产生判断误差，另外也说明C点本来由于温度梯度差已经存在热应力过分集中的现象，而局部直角结构则进一步增大了应力集中的效应，因此有必要对此点进行局部结构优化改进.

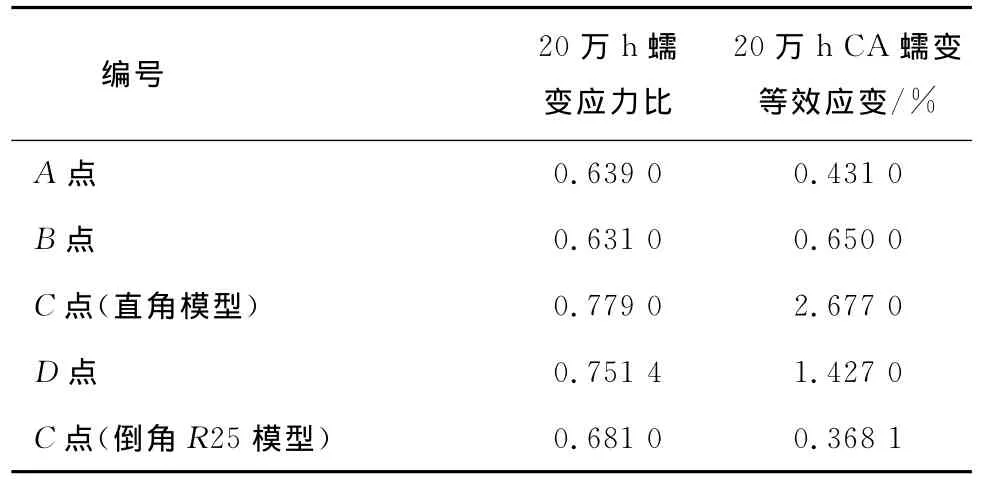
表1 高压外缸各点的蠕变计算结果Tab.1 Calculation results of CA equivalent creep strain for all points

3 高压外缸的结构改进

根据以上计算结果，虽然C点位置的应力比小于1（在许用范围内），但是其CA蠕变等效应变已经超过了许用值2%.从结构上看，C点附近存在一个直角（图3中圆圈位置），因而增大了C点处应力集中的影响，相应地增大了该点附近的应力与应变幅值，进而影响到该点的CA蠕变等效应变.为此，建议将此处结构改为对直角进行一个R25倒角设计，并对高压外缸进汽段（4）无倒角与有R25倒角的2种模型计算结果进行对比分析.

图6给出了2种不同模型20万h后的蠕变Mises应力比.从图6可知，由于其他部位结构尺寸没有变化，两者整体的应力分布趋势仍然一致.但是倒角R25模型在20万h后最大蠕变应力比有所下降，从0.7793（原模型）降低到0.6810（倒角R25模型），说明R25倒角有效降低了应力集中.图7给出了2种不同模型20万h后的CA蠕变等效应变.从图7可以看出，CA蠕变等效应变从原始模型的2.6670%降低到R25倒角模型的0.3681%，说明在该点处理上增加圆角降低了局部应力集中，对蠕变应变计算结果的影响相当大［11］.

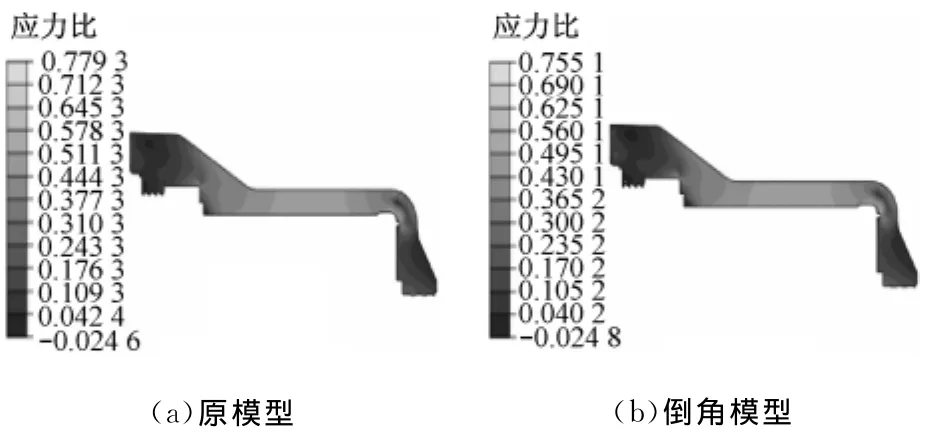
图6 2种模型20万h后的蠕变应力比对比Fig.6 Comparison of creep stress ratio between two models after 2×105 h

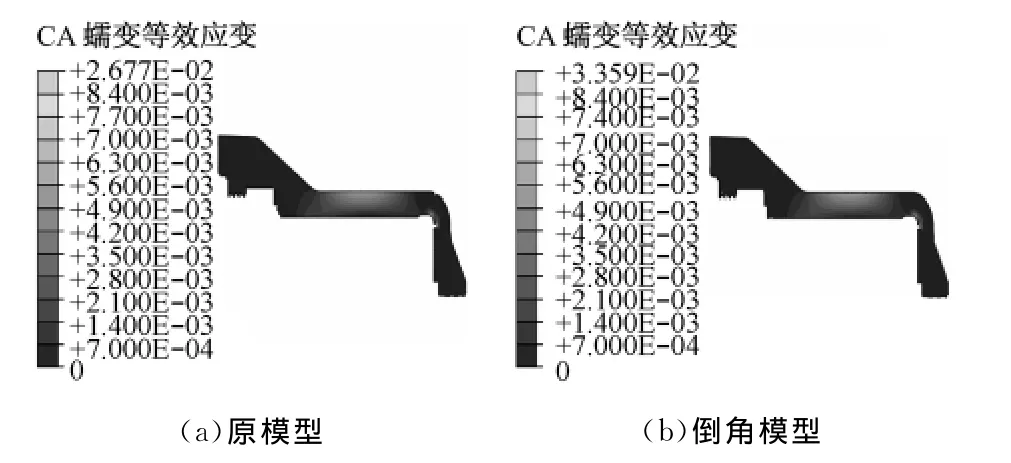
图7 2种模型20万h后的CA蠕变等效应变对比Fig.7 Comparison of CA equivalent creep strain between two models after 2×105 h

综上分析表明：在高压外缸进汽段拐角C点，原设计采用直角模型时，由于应力集中导致20万h后CA蠕变等效应变超过了工程许用值2%.在对高压外缸结构进行倒角R25优化后，20万h后蠕变应力比下降0.1左右，CA蠕变等效应变大幅降低，因此可以满足小于本文第一节提出的蠕变等效应变工程许用值2%的要求.

4 高压外缸的全三维高温蠕变计算

通常，轴对称二维模型计算的处理周期比较短，在方案初期可以利用轴对称二维模型来确定总体结构的合理性.但实际的高压外缸进汽段不完全是轴对称结构，在其两侧存在进汽口和猫爪、温度测点凸台等不规则形状区域，这些位置的实际应力和应变情况不能在二维模型上反映，所以要对高压外缸进汽段（4）模型进行全三维蠕变应力应变计算验证.但是，全三维结构的计算量非常庞大，难以在有限元计算中直接获取CA蠕变等效应变分布，一般在设计过程中只有结构基本确定后才进行全三维分析，然后根据计算获得Mises等效应变和CA较大的位置并结合二维计算发现的CA蠕变等效应变较大位置，再逐点验证其全三维计算CA蠕变等效应变.

4.1 20万h全三维蠕变计算Mises应力场

图8给出了高压外缸进汽段20万h后的全三维模型Mises等效应变分布.由图8可知，Mises等效应变最大区域与轴对称二维CA等效蠕变应变计算结果一样，都位于I型密封环区域D点，其Mises等效应变最大值为1.663%，比轴对称二维CA蠕变等效应变计算值1.427%略大.同时，计算结果表明，在过载阀和主汽阀的进口内侧位置E点和F点以及2个入口通道与缸体相贯位置G点和H 点也是Mises等效应变较大的位置，因此在全三维CA蠕变等效应变考核中应给予重点关注.

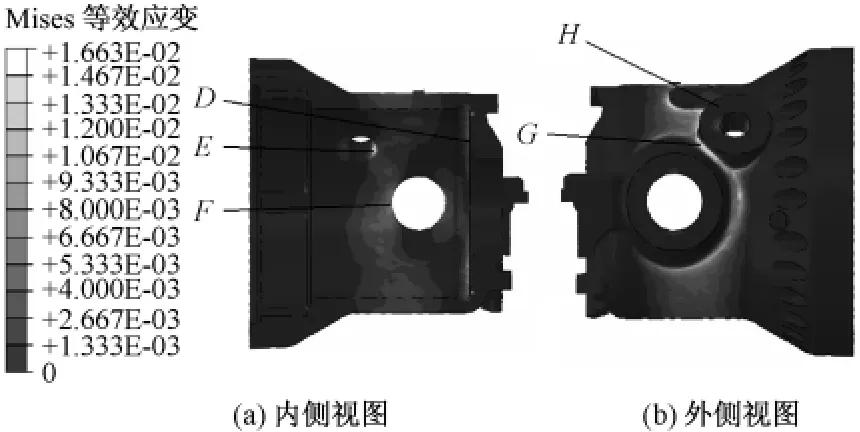
图8 全三维模型20万h后的蠕变Mises等效应变分布Fig.8 Mises creep strain based on 3Dmodel after 2×105 h

4.2 20万h全三维CA蠕变等效应变的考核

图9 全三维模型20万h后的CA系数计算结果Fig.9 Calculation results of CA coefficient based on 3D model after 2×105 h

图9给出了高压外缸全三维20万h后的多轴韧度系数CA的计算结果.从图9可以看出，高压外缸大部分区域多轴韧度系数CA小于或等于1，包括U型密封环区域C点和I型密封环区域D点以及上述E、F、G和H点重点考核位置的CA均在1～10的合理区间范围内.除此之外，CA大于或等于10的部位主要在高压外缸的猫爪和凸台等结构加强位置，这些点的工作温度都不在高温区域，CA过大主要是由于结构突变比较大而导致计算结果失真，因此从另一角度说明直接获取全三维CA蠕变等效应变场十分困难，因为在计算过程中还需要剔除这些CA系数失真的结构突变点.

结合图8和图9的计算结果，选取D、E、F、G和H5个点作为蠕变重点考核位置，并将这些点的全三维最大主应变以及对应的CA系数进行相乘，获取这些点的全三维20万h CA蠕变等效应变.图10给出了高压外缸全三维模型计算中CA蠕变等效应变的较大值.从图10可知，CA蠕变等效应变最大位置依然在I型密封环区域D点，其计算结果为1.49%，略小于二维计算结果的1.427%，但比全三维Mises等效应变1.663%要低，仍然小于本文推荐的工程许用值2%，证明该1000MW超超临界汽缸高温应变强度设计满足工程许用值要求.

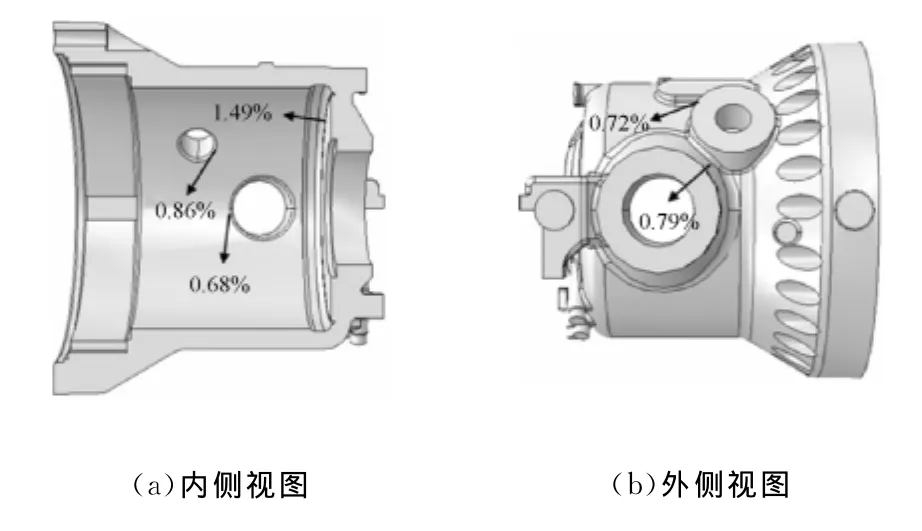
图10 全三维模型计算中CA蠕变等效应变的较大值Fig.10 Larger values of calculated CA equivalent creep strain based on 3Dmodel

5 结 论

（1）对于超超临界机组，不能只采用传统的蠕变断裂应力作为高温强度考核指标，推荐使用考虑多轴效应后的蠕变应变值作为补充的高温强度考核标准.

（2）推荐使用Norton－Bailey幂率方程表征材料的蠕变本构方程并引入CA多轴韧度系数，通过有限元计算方法获得的高压外缸结构的CA蠕变等效应变值能科学合理地反映部件在高温蠕变条件下的强度特征.

（3）将高压外缸直角结构进行R25倒角优化后，最大蠕变应力比下降到0.681，CA蠕变等效应变值大幅下降到0.3681%，说明局部应力集中对部件的蠕变变形影响较大.

（4）在轴对称二维CA蠕变等效应变计算结果的基础上，结合全三维Mises等效应变和CA计算结果能够找出比较危险的位置，并对其进行蠕变应变强度评估.

（5）1000MW超超临界高压外缸蠕变应变最大位置为I型密封环区域D点，二维计算获得的CA蠕变等效应变为1.427%，全三维计算获得的Mises等效应变为1.663%，全三维计算获得的CA蠕变等效应变为1.49%，均小于本文推荐的工程许用值2%，证明该高压外缸高温应变强度设计满足考核要求.

［1］ENO D R，YOUNG G A，SHAM T L.A unified view of engineering creep parameters［C］／／ASME Pressure Vessels and Piping Division Conference.Chicago，USA：ASME，2008.

［2］KEIENBURG K H，WIEMANN W，MUEHLE E E，et al.Selection of creep resistant steels and design criteria for large steam turbines［C］／／Indian National Symposium on Creep Resistant Steels for Power Plants.Hyderabad，India：［s.n.］，1983.

［3］NAUMENKO K， ALENBACH H.Modeling of creep for structural analysis［M］.Berlin，Germany：Springer－Verlag Berlin Heidelberg，2007.

［4］NAUMENKO K.Modeling of high－temperature creep for structural analysis applications［D］.Halle，Germany：Martin－Luther－Universit¨at Halle－Wittenberg，2006.

［5］YAO H T，XUAN Z H，WANG Zhengdong，et al.A review of creep analysis and design under multi－axial stress states［J］.Nuclear Engineering and Design，2007，18（10）：1969－1986.

［6］HUDDLESTON R L.An improved multiaxial creeprupture strength criterion［J］.Journal of Pressure Vessel Technology，1985，107（4）：421－429.

［7］涂善东，轩福贞，王国珍.高温条件下材料与结构力学行为的研究进展［J］.固体力学学报，2010，31（6）：679－695.TU Shandong，XUAN Fuzhen，WANG Guozhen.Recent progress in high temperature mechanical behavior of materials and structures［J］.Chinese Journal of Slid Mechanics，2010，31（6）：679－695.

［8］涂善东.高温结构完整性原理［M］.北京：科学出版社，2003.

［9］COCKS A C F，ASHBY M F.Intergranular fracture during power law creep under multiaxial stresses［J］.Metal Science Journal，1980，14（8）：395－402.

［10］HULL D，RIMMER D E.The growth of grain boundary voids under stress［J］.Philosophical Magazine，1959，42（4）：673－687.

［11］姚华堂，轩福贞，王正东，等.基于孔洞长大原理的多轴蠕变设计模型及其工程应用［J］.核动力工程，2007，28（3）：72－77.YAO Huatang，XUAN Fuzhen，WANG Zhengdong，et al.Multi－axial creep design models based on the cavity growth theory and its applications in engineering［J］.Nuclear Power Engineering，2007，28（3）：72－77.

［12］Nuclear Electric Plc.An assessment procedure for the high temperature response of structures，procedure R5issue［S］.Gloucester，UK：British Energy，1997.

［13］American Society of Mechanical Engineers.Boiler and pressure vessel code：Section III，Subsection NH Class 1［S］.New York，USA：ASME，1998.

［14］AINSWORTH R A，BUDDEN P J，DEAN D W，et al.Assessment of creep and creep－fatigue crack growth following the R5procedures［C］／／ASME Pressure Vessels and Piping Conference.Cleveland，USA，ASME，2003.

［15］ALTENBACK H，NAUMENKO K，GORASH Y.Numerical benchmarks for creep－damage modeling［C］／／Proceedings in Applied Mathematics and Mechanics.Zurich，Switzerland：WILEY－VCH Verlag GmbH ＆Co.KGaA，2007.

［16］WICHTMANN A.Evaluation of creep damage due to void growth under triaxial stress states in the design of steam turbine components［J］.JSME International Journal，Series A：2000，45（1）：72－77.