一种新的多光谱和全色图像的融合算法*

李龙澍，朱 超（安徽大学 计算机科学与技术学院，安徽 合肥 230601)

遥感图像融合是一种通过数字图像处理技术来融合两个或者两个以上遥感图像的技术。多光谱和全色图像的融合是遥感图像融合的一个特殊应用领域。一般地，图像融合可分为像素级融合、特征级融合和决策级融合。目前,很多图像融合方法都是在像素级融合方法基础上发展起来的,如HIS变换[1]、拉普拉斯金字塔变换和离散小波变换[2-3]等。

由于HIS变换融合方法计算简单，能极大地提高多光谱图像的空间分辨率，因而得到广泛的应用[1]。离散小波变换融合方法[2]直接舍弃了全色图像的低频分量,容易出现分块效应。平移不变离散小波变换克服了小波变换在分解信号时先滤波后抽样，重建信号时先插值后滤波的弊端，使得融合后的图像降低了偏差系数，提高了清晰度和空间分辨率[4-5]。本文结合了平移不变离散小波变换和HIS变换的优点，对多光谱图像的HIS变换的分量与全色图像进行SIDWT分解，然后高低频子图采用基于邻域特征值的融合规则，选取对应高低频系数，最后将SIDWT逆变换的结果进行HIS逆变换转换到RGB空间，得到最终的图像融合结果。

1 HIS变换和SIDWT变换

1.1 HIS变换

HIS反映了人的视觉系统感知色彩的方式，以色调(H)、饱和度(S)和强度(I)3种基本特征量来感知颜色,而且这三要素相关性很低。

式(1)、式(2)、式(3)为 HIS正变换公式，通过 HIS正变换可将图像变换到HIS空间中，得到H、S和I分量；式(4)是HIS逆变换公式，通过逆变换可将图像从 HIS空间转换到RGB空间。

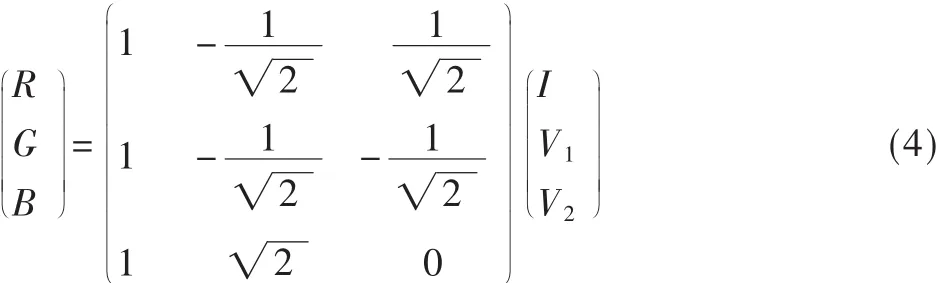
1.2 SIDWT变换

SIDWT正变换就是在小波变换时将输入序列分解为平移不变的小波来表示。SIDWT的每一步都将输入图像分解成小波序列 wi(n)和尺度序列 si(n)。将 wi(n)存储起来，而si(n)作为下一层分解的输入。分解公式为：

其中，s0(n)=f(n)。相对于标准的 DWT分解框架，SIDWT丢弃了一个高度冗余小波表示的子采样。通过在滤波器原型g(k)和 h(k)的序列间插入合适的 0值，即可得到第i 层的高通滤波器 g(2i·k)和低通滤波器 h(2i·k)。

SIDWT的逆变换是将具有平移不变性的小波序列wi(n)和尺度 序列 si(n)分别与合适的重 构滤 波器g˜(2i·k)和h˜(2i·k)求卷积，SIDWT 的逆变换公式为：

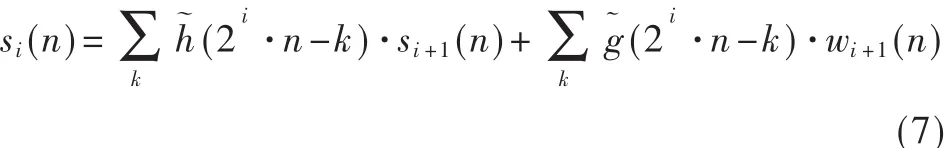
通过式(7)可实现重构输入序列f(n)。对于二维图像，其分解方法可以通过一维的分解方式分别在图像的行和列上连续进行得到。

2 基于邻域特征的图像融合新方法

HIS颜色空间的I分量是图像的强度表现，SIDWT能保留图像的边缘、轮廓和纹理等结构信息。因此，将HIS变换后的I分量与全色图像进行SIDWT变换，得到分解后的第j层低频部分和高频部分、、分别对低频和高频部分采取对应的融合规则,最终获取融合结果。

2.1 融合规则

在像素级融合中，融合规则一般采取对单个像素进行计算，使图像的每个像素点都孤立起来，没有考虑到区域结构的相似性，丢失了与周围像素点的相关性。因此，本文采取基于邻域像素特征的规则，这种规则是使用一个像素的一些邻域特征来指导该位置的系数选择。

2.1.1 低频部分的融合规则

本文采用参考文献[6]的融合规则和边缘分割的融合规则，以一个像素点为中心点的3×3窗口来考虑每个像素点。低频系数F(x,y)的融合公式为：

对于权重系数 λ1、λ2，对区域采用 Sobel边缘检测算子进行图像分割的方法来确定。假设B(x,y)为经过Sobel算子求得的像素点(x,y)的边缘特性值。对于检测结果中的孤立点，可能是由噪声引起的，可忽略不记。因此，去除孤立点的公式为：

其中，B(x,y)为通过Sobel边缘检测算子检测图像的边缘特征值。

根据整合后的分割结果来匹配两个子图的边缘信息，分为4种情况：

对于情况(1)和情况(2)，像素点只是其中一幅子图的边缘特征值，故分别是多光谱图像和全色图像所占的权重系数大；对于情况(3)，像素点均是两幅子图的边缘特征值，故两者所占的比例相同;情况(4)像素点均不是两幅子图的边缘特征值。因此，设置融合权重系数如下：情 况 (1)取 λ1=0.25，λ2=0.75； 情 况 (2)取 λ1=0.75，λ2=0.25；情况(3)取 λ1=0.5，λ2=0.5；情况(4)的权重选择采用对应两幅图像的平均梯度的比重作为权重系数的处理方法。本文通过计算两幅逼近图像的邻域平均梯度来确定权重系数，平均梯度计算公式为：

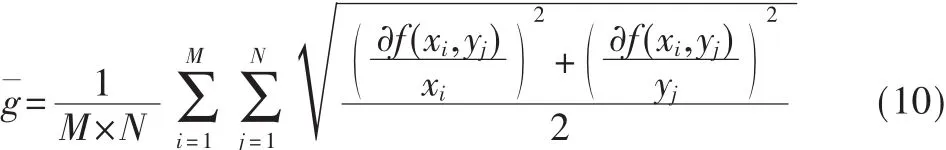
其中，M、N分别为区域窗口大小的长度和宽度，这里采用3×3的窗口。而权重系数的计算公式为：

2.1.2 高频部分的融合规则

高频部分包含了图像的显著细节特征，在高频部分的融合规则中，计算像素领域的方差来确定高频系数的选择。

2.2 融合步骤

本文算法的融合步骤如下。

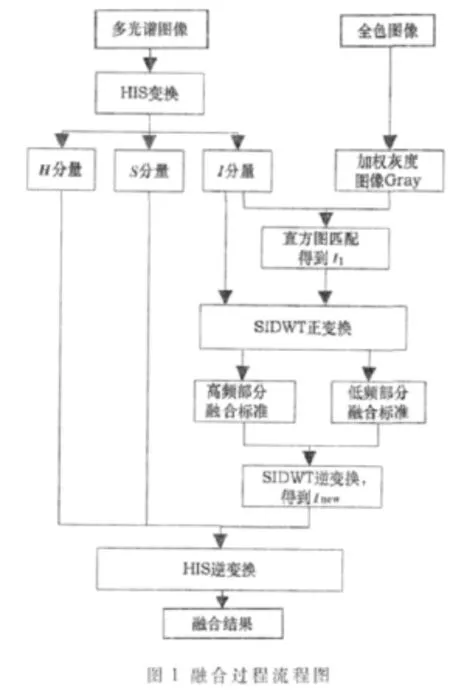
(1)将多光谱图像进行HIS分解,得到H、S和I分量。

(2)按分量I对全色图像的加权灰度图像进行直方图匹配，即将加权灰度图像映射到分量I的直方图空间，得到与 I相似直方图的 I1。

(3)将分量I和匹配后的I1按照一定的融合规则,进行SIDWT融合，得到融合结果Inew。

(4)将 H、S、Inew进行 HIS逆变换转换到 RGB空间，得到融合后的图像。

融合的流程图如图1所示。

3 实验结果与分析

3.1 多光谱和全色图像的融合结果

采用已配准的某场景低分辨率多光谱图像和高分辨率全色图像作为源图像实验数据进行融合，结果如图2所示。

从图2可以看出，HIS变换算法虽然分辨率得到了提高，但是产生了不同程度的光谱畸变；DWT算法由于在低频处理时丢失了全色图像的低频信息，导致融合图像中仅体现了较好的光谱信息，但是全色图像的分辨率没有有效地提高；SIDWT算法提高了图像的细节轮廓信息；使用本文算法得到的融合图像充分利用了多光谱图像的光谱信息和全色图像的细节信息。

3.2 融合结果质量评价

本文采用了均值、标准差、信息熵、平均梯度、空间频率和互信息常用的几种客观评价指标,对实验结果进行统计，结果如表1所示。可以看出SIDWT方法的标准差、信息熵、平均梯度和空间频率这些指标统计值优于HIS和DWT方法，但是均值和互信息方面没有得到有效提升；而本文方法在标准差、信息熵、平均梯度和空间频率方面高于其他方法的融合结果，而不足之处就是互信息的统计值低于HIS变换。

表1 本文图像不同融合算法的融合质量评价结果

本文结合了平移不变离散小波变换和HIS变换的优点，对多光谱图像的HIS变换的I分量与全色图像进行SIDWT分解，然后对得到的低频部分按照区域信息量、边缘信息和区域梯度等特征进行低频部分的融合，而对于高频部分采用局部方差最大的原则选取高频系数，最后将HIS逆变换转换到RGB空间，得到最终的图像融合结果。通过对比实验可以看出，本文方法的融合结果较理想，获得的融合图像综合了多光谱与全色遥感图像的互补性信息，在信息量、清晰度方面更优，丰富了光谱信息。

[1]黄金,潘泉,皮燕妮.基于区域特征加权的 HSI图像融合方法[J].计算机工程与应用,2005,41(6)：39-41.

[2]晁锐,张科,李言俊.一种基于小波变换的图像融合算法[J].电 子 学 报 ,2004,32(5)：750-753.

[3]任青,韩焱.基于小波邻域信息量的图像融合[J].微型机与 应 用,2010,29(4)：62-64.

[4]ROCKINGER O.Image sequence fusion using a shift-invariant wavelet transform[C].Processings of IEEE International conference on Image Processing,1997.

[5]余连生,文贡坚,李智勇.基于 SIDWT的遥感图像融合算法[J].计 算 机 工 程 ,2011,37(17)：197-199.

[6]TIAN J,CHEN J,ZHANG C.Multispectral image fusion based on fractal feature[C].Prosceedings of SPIE,2004,5308：824-832.