氩流体扩散行为的分子动力学模拟研究

李 群 ，王宝和

(大连理工大学化工学院，辽宁大连 116024)

扩散系数是表征物质运输过程的重要参数，但采用常规实验手段很难准确测量得到。对于受限空间的流体，扩散系数的研究更加困难。随着计算机和分子动力学模拟技术的发展，从分子水平研究流体的扩散规律已经引起了国内外许多学者的极大关注［1－3］。Meier等采用平衡分子动力学方法，模拟得到了Lennard－Jones(L－J)流体的自扩散系数和黏度［2］。葛宋和陈民采用平衡分子动力学方法，通过均方位移计算得到了超临界条件下，L－J流体的自扩散系数随温度的变化规律;同时，利用Green－Kubo法计算了超临界L－J流体混合物的扩散性质［4］。本文拟采用L－J模型，探究非受限空间中温度、截断半径、模拟粒子数和受限空间中能量系数 、狭缝宽度及温度对氩流体自扩散系数的影响。

1 模拟方法

目前，采用分子动力学模拟技术，计算自扩散系数的方法主要有两种，即Green－Kubo法和Einstein法，分别如式(1)和(2)所示［1］。本文采用Einstein法计算氩流体的自扩散系数。

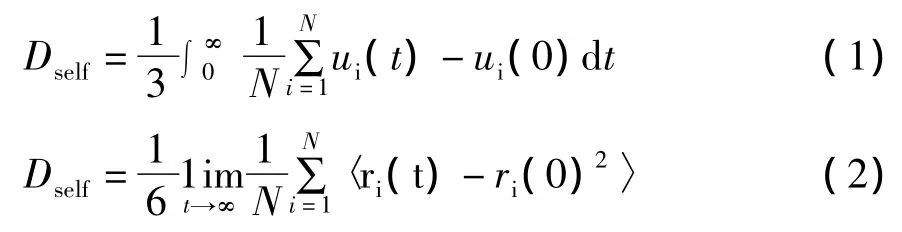
式中，Dself为自扩散系数，m2/s;N为粒子总数;ui(t)和ui(0)为第i个粒子在t和0时刻的速度，m/s;ri(t)和ri(0)为粒子i在t和0时刻的位置，m;t为时间，s;〈*〉表示系综平均。

1.1 非受限空间模拟体系的建立

非受限空间的模拟盒子如图1所示。在模拟的初始时刻，氩流体粒子以面心立方晶格(FCC)均匀分布在边长为L的正方体模拟盒中。模拟过程中，系统采用正则系综(NVT)，并不断调整体系质心使之处于坐标原点;控温方式采用Nose－Hoover控温法;在x、y、z方向上均采用周期性边界条件。

1.2 受限空间模拟体系建立

对于受限空间的分子动力学模拟(图1a)，壁面有着极其重要的作用。壁面大致分为虚拟热壁面和结构壁面。在虚拟热壁面体系中，不考虑壁面的微观粒子结构和壁面与流体之间的相互作用，入射到壁面的流体粒子被弹回到流体系统，流体粒子弹回速度的大小和方向由壁面的温度和粗糙度决定。结构壁面模拟真实壁面的原子晶格结构，除了要考虑流体粒子自身两两相互作用外，还要考虑流体粒子与壁面粒子的相互作用。结构壁面又分为刚性壁面，Phantom壁面和Einstein固体壁面［5］。

本文受限空中的壁面是由固定不动的虚拟LJ原子组成的刚性壁面，模拟盒子如图1b所示(上面和下面的三层原子为壁面原子，中间夹层的六层粒子为氩原子)。与非受限空间一样，在受限空间中也采用正则系综(NVT)。x和z方向为周期性边界条件，y方向为固体壁面边界条件。

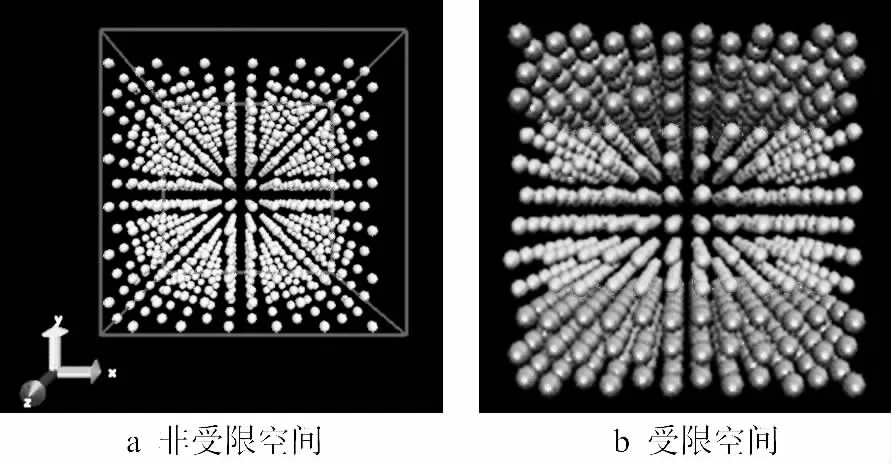
图1 空间模拟体系的示意图

1.3 势能模型的选取

分子动力学模拟结果的准确性，主要取决于描述分子间作用力的的势能函数;因此，选择合适的势函数至关重要。势函数可分为对势与多体势。本文采用L－J(12－6)对势函数，如式(3)所示。

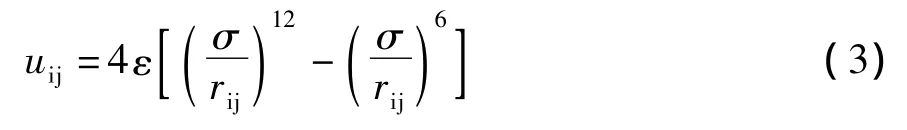
式中:uij为对势势能，J;ε能量参数，J;σ长度参数，m;rij为粒子i与j之间的距离，m。在本文中，流体与固体壁面之间的L－J势能函数如式(4)所示。

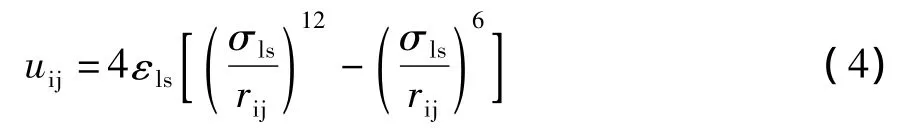
式中:εls、σls分别表示流体粒子和固体壁面粒子之间的能量参数和距离参数，分别由式(5)和(6)确定。

式中:下标l为氩流体，s为固体壁面，ls为固体壁面与氩流体的相互作用势能参数，α为壁面粒子与流体粒子相互作用能量系数(本文简称为能量系数)，β为壁面粒子与流体粒子相互作用长度系数，本文β取1.03来研究壁面粒子能量系数α对氩流体在受限空间中自扩散系数的影响［6］。氩流体的σAr－Ar=0.3405 nm，εAr－Ar/kB=119.8 K。

1.4 模拟体系的运算

在分子动力学模拟中，需要对各物理量进行无量纲化，如表1所示。表中，上标*代表无量纲的物理量;kB为波尔兹曼常数，1.3810－23J/K;m 为质量，kg;T为温度，K;ρ为密度，kg/m3;H为狭缝宽度，m。初始速度由速度发生器随机给定，控温方法为Nose－Hoover控温法。时间步长为2fs，总模拟时间400 ps，总步数为200000步，每1000步输出一个数据。本文模拟数据均采用LAMMPS(Largescale Atomic/Molecular Massively Parallel Simulator)软件计算得到。

表1 物理量的无量纲化

2 模拟结果与讨论

2.1 非受限空间的氩流体自扩散系数

2.1.1 截断半径对自扩散系数的影响

在粒子数Num=864，温度T=90 K条件下，对截断半径 rc=0.85、1.02、1.19、1.36、1.53、1.70 nm进行分子动力学模拟，得到粒子的均方位移(MSD)，再由均方位移计算得到氩流体的自扩散系数(每个条件进行三次模拟计算，并取其平均值)，结果如表2所示。从表2可以看出，所有模拟值与实验值的相对误差都小于7%。其中rc=1.36 nm时，模拟值与实验值最接近，相对误差为0.41%，因此，下文均取截断半径rc=1.36 nm进行模拟计算。

表2 截断半径对氩流体自扩散系数的影响

2.1.2 粒子数对自扩散系数的影响

在T=100 K，截断半径rc=1.36 nm的条件下，粒子数 Num=256、500、864、1372 和2048 时的氩流体自扩散系数如表3所示。由表3可知，模拟平均值与实验值的相对误差均小于10%，且随着粒子数增大，相对误差的绝对值逐渐减小，由此可知，随粒子数增加模拟结果越接近于实验值。但模拟耗时随着粒子数增多急剧增大，综合考虑计算时间、计算机内存和相对误差，下文中的模拟粒子数均采用864。

表3 粒子数对氩流体自扩散系数的影响

2.1.3 温度对自扩散系数的影响

在粒子数Num=864，截断半径rc=1.36 nm，温度 T=90、100、110、120、130 K 时，氩流体的自扩散系数模拟结果如表4所示。由表4可见，随着温度升高，自扩散系数逐渐增大。各温度的自扩散系数模拟值和实验值基本吻合，除130 K外相对误差都在10%以内，但越接近于临界状态，自扩散系数的模拟误差越大。

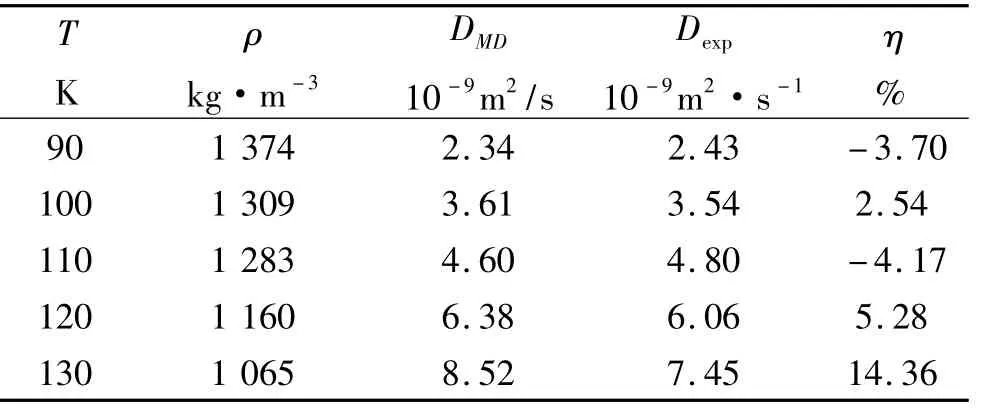
表4 不同温度下氩自扩散系数模拟结果

可见，氩流体的自扩散系数随温度的升高而增大。假定氩流体的自扩散系数与温度的关系服从Arrhenius方程(8)［7］。

式中，D0为极限自扩散系数，m2/s;E为扩散活化能，J/mol;R气体常数。

对式(8)取对数得到式(9)。可见，lnD与1/T呈线性关系，其斜率为－E/R，截距为1nD0。如图2所示，直线斜率为－E/R=－3.695，计算得到自扩散活化能 E 为3072.19 J/mol;截距 1nD0=4.945，则其极限自扩散系数D0为139.77×10－9m/s2。因此，可以认为氩流体的自扩散系数与温度的关系符合Arrhenius方程。

图2 lnD与1/T关系曲线

2.1.4 径向分布函数

径向分布函数g(r)可以直接反映物质分子的聚集特性。在粒子数Num=864，rc=1.36 nm条件下，对 T=90、100、110、120、130 K 的氩流体体系进行模拟，得到粒子的径向分布函数图像如图3所示。由图3可以看出，当r＞4.0σ时，各图中径向分布函数的值都趋近于1，r＞0.9σ时径向分布函数的值均为零，这表示该流体系统中分子与分子之间的最近距离不可能小于0.9σ，而且当分子间的距离超过4.0σ时，与均匀流体性质相同。此外，径向分布函数的最大峰值均出现在r约为1.2σ处，这表明离分子1.2σ处附近出现其他分子的概率最大，此处的区域密度最大，但峰值却随着温度升高而减小。

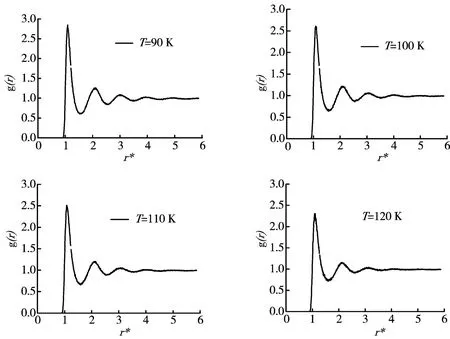
图3 不同温度下氩流体的径向分布函数

2.2 受限空间的氩流体自扩散系

2.2.1 能量系数对自扩散系数的影响

当狭缝宽度 H=2.99nm，rc=1.36 nm，能量系数 α =0.1、0.6、1.0、3.0、5.0、7.0 时，模拟得到的氩流体自扩散系数如图 4所示(T=90、100、110、120 K)。由图4可见，随着温度增大，氩流体自扩散系数逐渐增大，但随着能量系数的增大，自扩散系数逐渐减小。

图4 能量系数α对自扩散系数的影响

2.2.2 狭缝宽度对自扩散系数的影响

在温度T=100 K，rc=1.36 nm，狭缝宽度 H=2.99、4.11、5.28、6.45、8.21 nm 的条件下，模拟得到的氩流体自扩散系数如图5所示。从图中可以看出，随着狭缝宽度的增大，氩流体自扩散系数逐渐增大，且增大趋势渐趋于平缓，最终接近于非受限空间中的自扩散系数。

图5 狭缝宽度对氩流体自扩散系数的影响

2.2.3 温度对自扩散系数的影响

在狭缝宽度 H=2.99 nm，rc=1.36 nm 的受限空间中，当温度 T=90、100、110、120、130 K 时，氩流体自扩散系数的模拟结果如图6所示，并与非受限空间中自扩散系数的模拟值及实验值进行了比较。从图6可见，在受限条件下，氩流体自扩散系数的模拟值与实验值都随着温度升高而增大，氩流体自扩散系数模拟值随温度的变化也满足Arrhenius关系，计算得到的自扩散活化能E=2362.85 J/mol，极限自扩散系数D0=51.21×10－9m2/s。但在相同温度的条件下，受限空间氩流体的自扩散系数比非受限空间的要低。

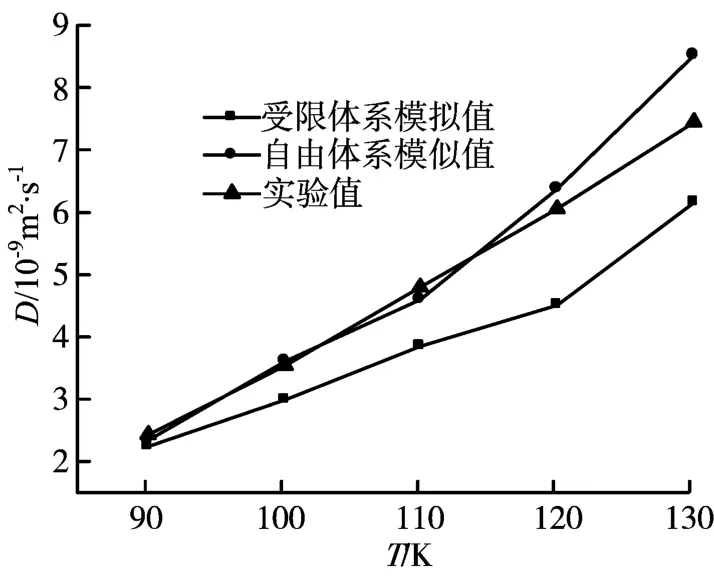
图6 温度对受限空间氩流体自扩散系数的影响

3 结论

本文采用分子动力学模拟方法，考察了非受限空间中截断半径、粒子数、温度等和受限空间中能量系数、狭缝宽度及温度等对氩流体自扩散系数的影响，并得到了不同温度下氩流体的径向分布函数。通过对模拟结果的分析，得到以下结论:

在非受限空间中，随温度T升高，自扩散系数增大，且符合Arrhenius方程，自扩散活化能为 3072.19 J/mol。

在受限空间中，随着能量系数α的增大，氩流体的自扩散系数逐渐减小;随着温度的升高，氩流体的自扩散系数增大，且满足Arrhenius方程，扩散活化能为2362.85 J/mol;随着狭缝宽度的增加，氩流体的自扩散系数也逐渐增大，最后趋于实验值;在相同温度的条件下，受限空间氩流体的自扩散系数比非受限空间的要低。

［1］Allen M P，Tildesley D J.Computer simulation of liquids［M］.Oxford:Oxford University Press，1987.

［2］Meier K，Laesecke A，Kabela S C.A molecular dynamics simulation study of the self－diffusion coefficient and viscosity of the Lennard － Jones fluid［J］.International Journal of Thermophysics，2001，22(1):161 －173.

［3］严六明，严琪良，刘洪来.Ar－Kr溶液扩散系数的分子动力学模拟及其与温度的关系［J］.高等学校化学学报，1997，18:2026 －2029.

［4］葛 宋，陈 民.超临界L－J流体混合物互扩散性质的分子动力学模拟［J］.高等化学学报，2011，32:2593－2597.

［5］曹炳阳.速度滑移及其对微纳尺度流动影响的分子动力学研究［D］.北京:清华大学航天航空学院，2005.

［6］秦 星，张秉坚，张 晖，等.微孔中简单流体混合物自扩散系数的分子动力学模拟与关联［J］.化学物理学报，2003，16(6):467 －471.

［7］方俊鑫，陆 栋.固体物理学［M］.上海:科学技术出版社，1981.