基于时间序列模型预测汽车销量研究

郭顺生，王磊，黄琨

（武汉理工大学 机电工程学院，武汉 430070）

1 引言

2013 年初，中国汽车工业协会信息发布会在京召开。中国汽车工业协会副秘书长师建华发布了2012 年汽车市场运行情况概述及2013 年汽车市场形势预测。数据显示，2012 年全国汽车产销1927.18 万辆和1930.64 万辆，同比分别增长4.6%和4.3%，比上年同期分别提高3.8和1.9个百分点。我国汽车的销量再创新高，稳居全球产销第一。

虽然我国2012 年的汽车销售量很好，但是也的确暴露出了很多的问题。例如，很多制造商在上半年对于整个汽车销售市场盲目乐观，造成了2012 年汽车市场高库存的局面,最后演变成了大打价格战的结局，对整个汽车销售市场产生了巨大冲击和影响，这一教训在制定2013 年汽车销售目标时，能否吸取教训还难说，能否客观、冷静、实际地制定2013 年计划，也很难说。

汽车的销量也就是汽车的增加量，可以准确地反映人们对汽车的需求。相比于以往文章中预测我国汽车市场的年销售情况，本文引入时间序列模型，以月份为单位，对2013 年上半年整个中国汽车市场的月销量进行了一个预测，这样更有利于企业根据每个月份的预测结果快速地调整库存以及整个供应链，从而更好地适应市场变化。

本文尝试用自回归移动平均模型（ARMA）通过Eviews软件［1］，建立我国汽车销量预测模型，希望可以对企业在根据预测值进行产量和库存安排的同时、及时地调整市场战略提供一定的帮助。此外，政府相关部门在交通布局、道路整改、停车位增设、城市绿化等政策的制定上参照预测结果进行相应调整。

2 ARMA 模型概述

ARMA 模型全称为自回归移动平均模型（Auto-Regressive Moving Average Model，简称ARMA），是由Box和Jenkins 于1970 年代初提出的著名时间序列预测方法，又称为box-jenkins 模型、博克思-詹金斯法［2］。ARMA 模型可分为三种类型：自回归（AR:Auto-Regressive）模型、移动平均（MA：Moving-Average）模型和自回归移动平均（ARMA：Auto-Regressive Moving-Average）模型［2］。

（1）AR 模型。时间序列用前期值和随机项的线性函数表示，是系统对过去自身状态的记忆。p阶自回归模型记为AR（p），其式为［3］：

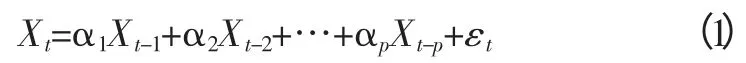
（2）MA 模型。用当期和前期的随机误差项的线性函数表示，是系统对过去时刻进入系统的噪声（随机扰动项）的记忆［3］。q阶移动平均模型记为MA（q），其式为：

其中，εt为随机扰动项。

（3）ARMA 模型。用当期和前期的随机误差项以及前期值的线性函数表示，是系统对过去自身状态以及进入系统的噪声的记忆［3，4］。ARMA（p，q）的形式为:

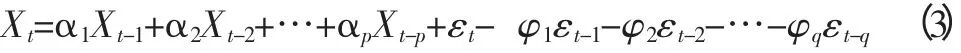
3 ARMA 模型的建立与检验

3.1 时间序列平稳性分析

集合ARMA 模型的使用条件，选用2009 年1 月到2012年12 月中国汽车月销售量，见表1，构成时间序列｛sh｝。

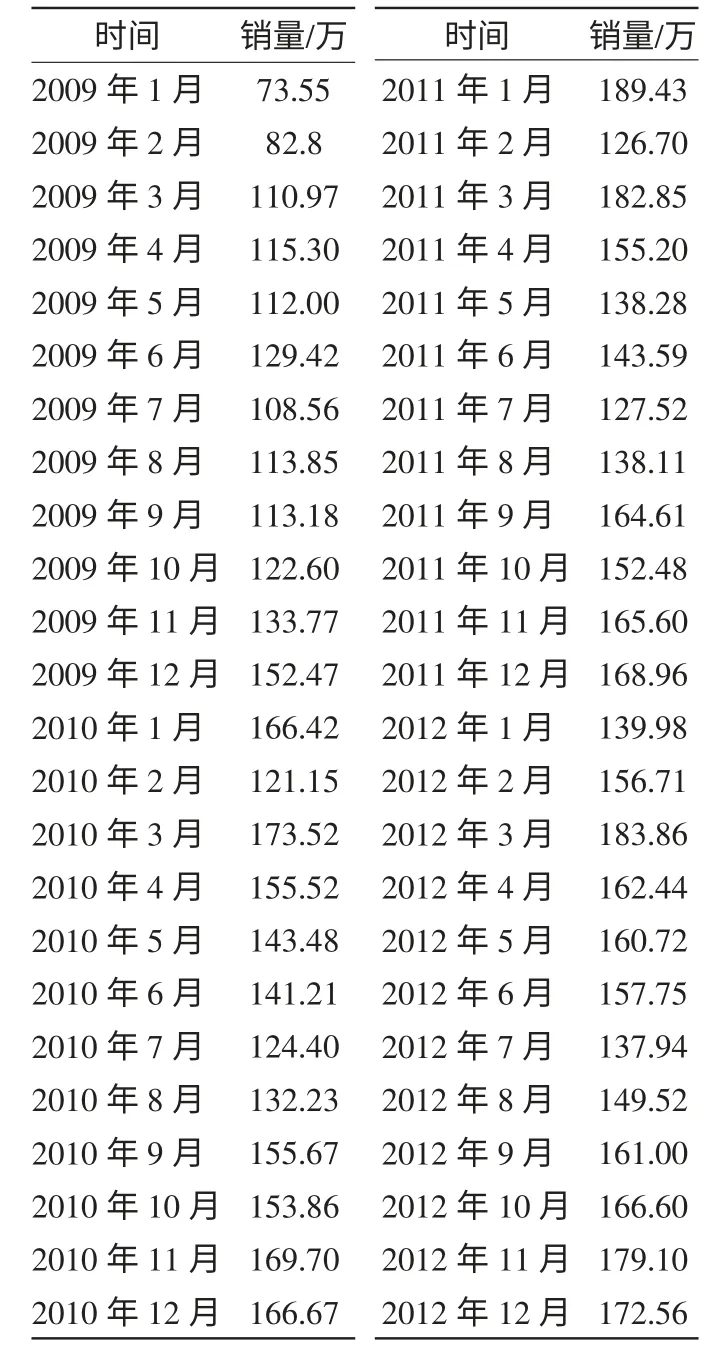
表1 2009 年1 月-2012 年12 月中国汽车月销量

根据表1中的时间序列，做出中国汽车月销售量时间序列图（见图1），由图1 可以看出该序列自2010 年之后有明显的季节性规律，每年的年初和年末，汽车销售量都会较高，而年中则会比较低靡。并且在2 月份，由于过年放假的原因，汽车销售市场也会冷淡，所以每年的前三个月波动会比较大。根据图1，做出时间序列｛sh｝的自相关以及偏相关函数图（图2），由于序列的自相关系数不是很快地（如滞后期K=2，3）趋于零，即缓慢下降，表明序列是非平稳的。

图1 序列｛sh｝走势图

图2 序列｛sh｝的自相关及偏相关分析

因非平稳序列｛sh｝存在异方差，且2009年的数据对于季节性很不明显，因此除去2009 年，并对序列｛sh｝取 对 数做差分运算再进 行 ADF 检验，经过差分运算后，记时间序列为｛sh1｝，该序列的自相关系数（图3）很快地趋近于零，可初步表明该序列为平稳序列。

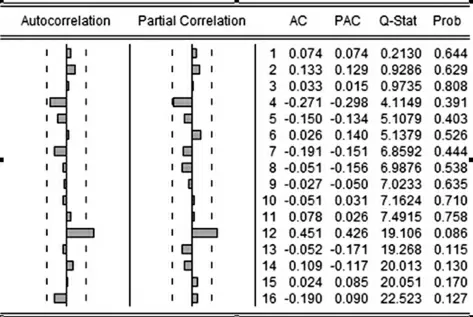
图3 序列｛sh1｝的自相关及偏相关分析

将该序列进一步进行ADF 检验（表2），原假设为该序列存在单位根，而检验结果t 统计量值为-5.748626，低于显著水平为1%的临界值。这表明可以在99%的置信水平下不接受原假设，也就是该序列｛sh1｝不存在单位根，是平稳序列。

表2 序列｛sh1｝的ADF 检验

3.2 模型识别及定阶以及检验

通过图3 判断，该序列在滞后期12 处的自相关系数和偏相关系数显著异于零，因此可认为该序列存在一个周期为12的季节性变动。建立模型时，可在模型中加入周期为12的SAR 或SMA 项。

而AC 在滞后期k＞4和PAC 在滞后期k＞5 时出现结尾现象，具有ARMA 模型的特征，同时采用Akaike 提出的AIC 准则和Schwartz 提出的SC 准则，对序列｛sh｝的ARMA 模型进行逐步比较定阶。当p=2，q=5 时，达到可以取得的最大值（R2＝0.994596），AIC 与SC的一组值达到最小值（AIC=-5.912577，SC=-5.467391）。对该模型的残差序列｛ε1｝进行自相关分析（图4），由图中可看出残差序列的自相关系数都均匀的分布在置信区间内，并趋近于零，这表明该序列通过白噪声检验。由上述分析可确定｛sh｝ 适合ARMA（5，2）模型。

图4 序列｛εt｝的自相关及偏相关分析

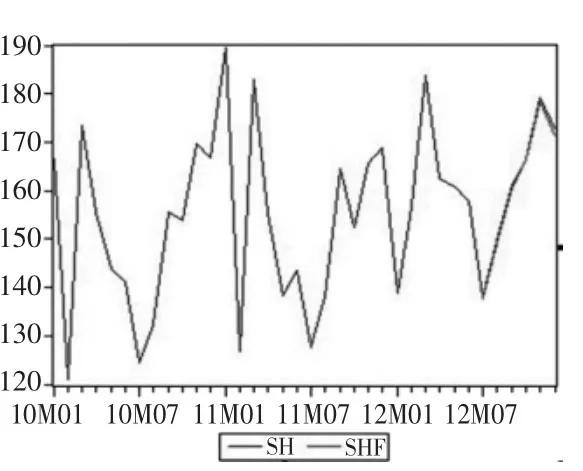
图5 2012 年下半年预测结果与真实结果

3.3 模型的评估

利用该模型预测2012 年7 月 到2012 年12 月汽车月销量，与真实值拟合（图5，表3），由图中可以看到预测结果与真实结果拟合度非常好，预测误差也都控制在了3%以内，而预测结果的Theil 不等系数为0.002075，因此认为该模型预测在短期内具有较高的精度。

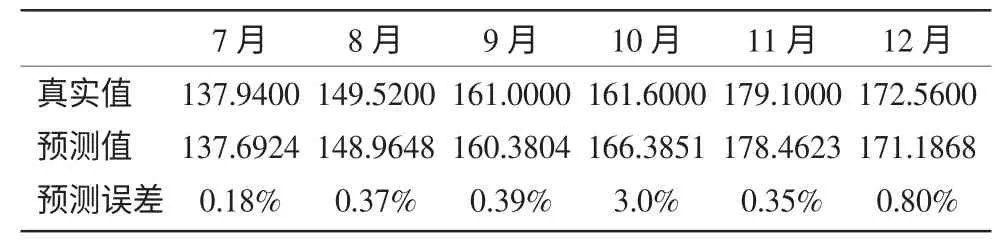
表3 2012 年下半年预测结果与真实结果

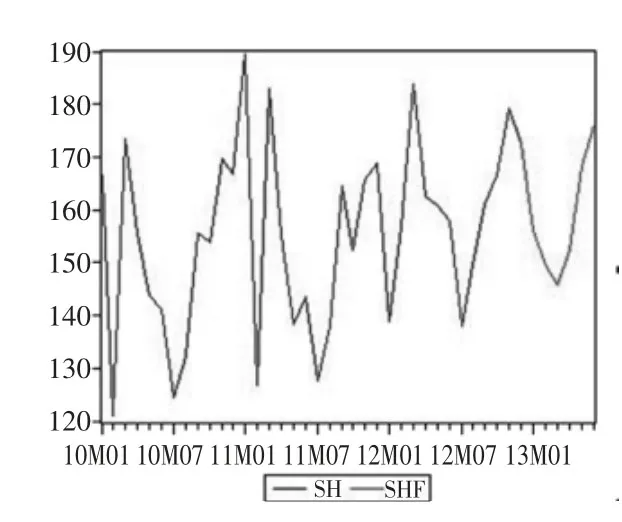
图6 2013 年上半年预测结果

4 模型的预测

由于该模型在短期内具有较高的精度，且不利于长期预测，因此将扩展样本至2013 年6 月，利用ARMA（5，2）模型，以及2009 年1 月到2012 年12 月的有关数据，对2013 年上半年汽车月销量进行预测，结果如图6、表4所示。

表4 2013 年上半年预测结果

5 结语

通过ARMA（5，2）模型预测的结果表明，2013 年上半年中国汽车销量会有一个先降后升的趋势，但是由于原时间序列较少，对预测精度是一个不利的影响，本次预测只考虑了历年数据的变化趋势，没有考虑市场中一些随机因素，如节能减排的压力以及世界经济的影响，求出的预测值只是一个大概值，因此笔者认为如果考虑将ARMA 模型与其他模型混合使用，同时考虑时间序列以及随机因素并且增加样本，那么应该优于此模型，并大大提高预测精度。

［1］李敏，陈胜可.Eviews 统计分析与应用［M］.北京：电子工业出版社，2011：112-142.

［2］LIM C,et al.Forecasting h（m）otel guest nights in New Zealand［J］.International Journal of Hospitality Management，2009（28）：228-235.

［3］李根，赵金楼，苏屹.基于ARMA 模型的世界集装箱船手持订单量预测研究［J］.科技管理研究，2012（16）：217-220.

［4］卢小丽，何光.基于ARMA 模型的四川省农村居民收入趋势预测［J］.中国农学通报，2012，28（5）：110-114.