基于数据预处理的DDoS攻击检测方法研究*

高一为,赖英旭,吴 欢,陈伟桐

（北京工业大学 计算机学院，北京 100124）

现有的基于网络流量的DDoS攻击检测方法可以按照对时间尺度的敏感程度进行划分,通常将小于100 ms的网络模型称为小尺度网络模型，将以小时(hour)或天(day)作为时间单位的网络模型称为大尺度网络模型。基于大尺度网络模型的检测方法主要有方差分析法(ANVOA)[1]、泛化似然比检验法(Generalized Likelihood Ratio Test)[2]、自适应残差比较法[3]等，这些方法虽然有较好的检测率和较低的误报率，但是因其以hour或day为统计单位而不具备实时检测的能力。相比之下小尺度网络模型更适合于实时检测，但因其表现出多分形性[4]而难以观测。参考文献[5]提出的Holder指数检测法虽然检测延时短，但是受到短相关性质对网络流量整体观测能力不足的影响，误报率过高。针对这一问题，参考文献[6]提出了一种基于传统Hurst指数和Holder指数的分形检测法，通过判断网络流量的实时分形特性,分别采用两种不同方法进行检测，虽然提高了分形模型中长相关部分的检测准确率，但是当流量数据表现出短相关时，误报问题仍没有解决。参考文献[7]提出了一种基于Hurst指数的方差-时间图法VTP(Variance-Time Plots)，试图利用多分形模型中包含的长相关特性进行检测。受多分形模型中长相关特性并不明显的影响，误报率虽然有所下降，但是检测率上还存在不足。

现有小尺度网络模型通常采用Holder、Hurst等指数进行检测，Holder指数观测尺度狭窄、误报率高；Hurst指数能够在整体上对流量的自相似性进行刻画，具有较高的检测精度，但要求观测的时间尺度宽，不利于实时检测。本文提出的基于数据预处理的DDoS攻击检测方法在Hurst指数检测的基础上，通过提高流量间相关度，满足了Hurst指数定义对模型长相关程度的要求，从而能够更准确地对具有多分形特性的流量进行分析。

1 流量预处理

小尺度网络模型中包含的网络业务信息相比大尺度网络模型少但更为细致，因而也更易受流量的突发性影响。基于流量的DDoS攻击检测技术正是利用了流量突发性对统计特性造成的奇异点进行检测，因此为了降低误报率就需要降低正常流量发生时对小尺度模型统计特性的影响。最直接的方法就是增加小尺度模型各节点包含的信息量，增强其长相关性。参考文献[8]就可能影响流量性能的因素提出了假设，并认为均值和方差对多分形有较大影响。本文在参考文献[8]的基础上，提出采用滑动平均值来代替原有采样值的方法，在保证不丢失原有信息特性的前提下，将前后时间节点的特性包含进来，提高了节点中包含的信息量，使得小尺度网络模型的长相关性增强，同时降低了正常流量发生时对统计特性可能造成的影响。流量预处理方法如式(1)所示：

式中，t(n)为进行预处理前时间序列；g(n)为采用滑动平均变换后的时间序列；m为增加关联度的权系数，m值越大，经过预处理后的时间序列长相关性质越强。

2 DDoS攻击检测方法

2.1 数据预处理

利用式(1)，将参数 m设为 100，从时间序列 t(n)中取100个序列值(总时长为1 s的流量数据)，作滑动平均计算得到序列g(n)。

2.2 小波分解

由于传统的模型和分析工具不适用多分形模型，本文利用小波分解法对小尺度网络模型进行分解获得网络流量的高频系数（或称细节系数），为求解Hurst指数提供基础。 将 g(n)分为 i个子区域 g′(n),i=1,2,…,n,如式(2)所示：

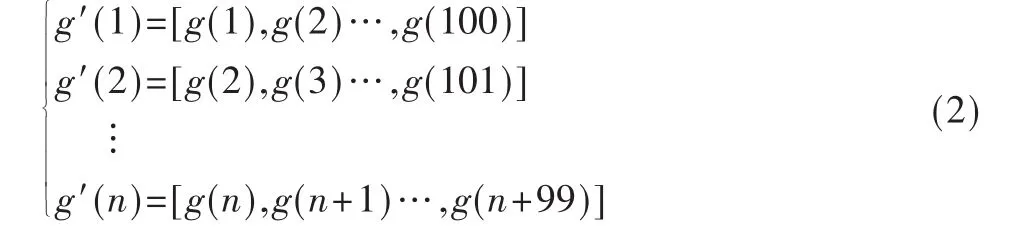
每次获得的新采样数据插入到序列末尾，这种序列构造方式减少了获取定长数据的等待时间,提高了构造速度。

第i个子区的j级分解低频系数 (或称为近似系数)和j级分解高频系数(或称为细节系数)分别用 aig(j,k)和dig(j,k)表示,如 式(3)所 示:

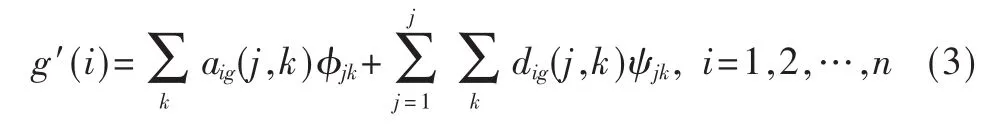
其中j为小波分解层数，k为小波的移动尺度，φjk为小波尺度函数，ψjk为小波函数。

[9,10]的研究表明，消失矩与小波分解求自相似参数Hurst的准确性有着密切关系。根据参考文献[9]中的研究结果，db小波（Daubechies）在求解 Hurst值的过程中准确性普遍优于一般方法（如R/S）。因此本文选取db(3)作为小波消失矩，小波分解层数为j=10，小波移动尺度k=1。

小波分解过程中通常采用二进制伸缩的方式,如式(4)所示:

2.3 Hurst指数求解

参考文献[11]中的研究表明，利用小波高频系数dig(j,k)求解Hurst指数的方法主要有方差法、谱估计法和能量法等。本文选择方差法求解Hurst指数,如式(5)所示:

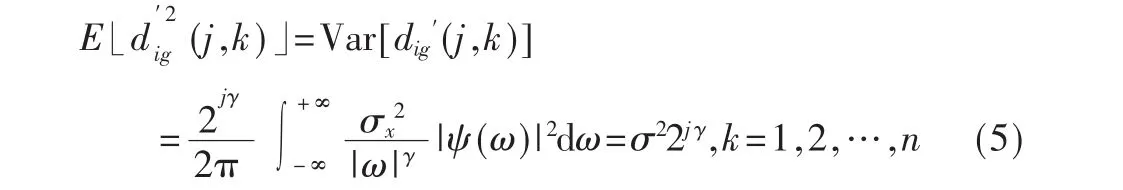
根据式(5)的定义对小波高频系数（或称细节系数）dig(j,k)做零值化处理，以达到均方误差最小的目的，如式(6)所示。

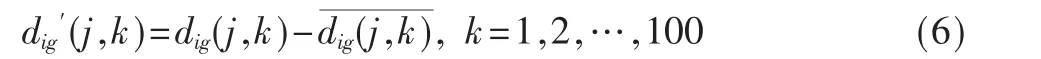
经过小波变换分解和零值化处理后,通过对式(5)两边取对数进行线性拟合,如式(7)所示：

得到以 j为自变量，以 log2Var⎿dig′(j,k)」,k=1,2,…,100 为函数的直线，其斜率b=2H+1，即为Hurst指数。

2.4 Hurst指数阈值设定

对于小尺度网络模型而言，当平稳的DDoS攻击流量发生时，网络流量整体的波动性下降，突发性减弱，自相似性增强。经过本文提出的预处理方法处理，Hurst指数升高并趋于平稳。本文方法正是利用这一原理对DDoS攻击进行检测，并通过计算方差的方法来检测Hurst指数的平稳性。

本文提出,对经过预处理的流量采用Hurst指数方差平均值 Var[H′]来量化其变化程度，如式(8)所示。

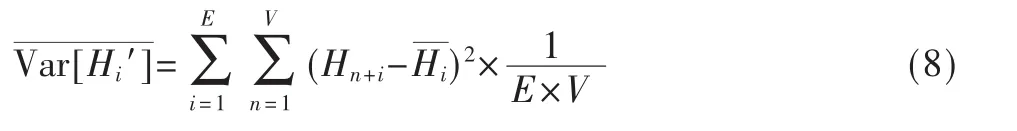
式中E为计算平均值的尺度大小，V为计算方差的尺度大小。E和V的选取将会对算法的检测延迟和误报率产生影响。取值越高,观测越准确，误报率越低，但也会造成检测延迟上升。相反则会降低检测延迟，提高误报率。在此本文将阈值设定为

3 DDoS攻击检测实验

本文采用模拟攻击的方法对文中提出的网络异常检测算法进行测试。

3.1 数据来源

实验数据由正常的背景流量和模拟的攻击流量汇聚而成。

以北京工业大学某楼层的真实流量为正常流量样本，采用Wireshark截取上午 10：30～11:17之间的全部流量。时间精度为1 ms,包括各类正常访问的数据包1 620 400个。分别汇聚为精度10 ms的BJUT-10流量和精度为1 s的BJUT-1000流量。

利用Sprient公司的ThreatEx2600作为攻击流量的产生工具，模拟了DDoS攻击中最经典的SYN-Flood攻击流量，并将攻击强度以1 000 threats/s的幅度逐渐增加。将攻击行为分为两次，分别在小背景流量和大背景流量下进行，小背景流量攻击发生在100 000 ms，大背景流量发生在200 000 ms。每次攻击持续180 s，其中流量上升阶段30 s，峰值攻击 120 s，流量下降阶段30 s。测试环境如图1所示。

3.2 检测实验

通过第2.3节中所描述的检测算法对实验数据进行检测，Hurst值的结果如图2所示。

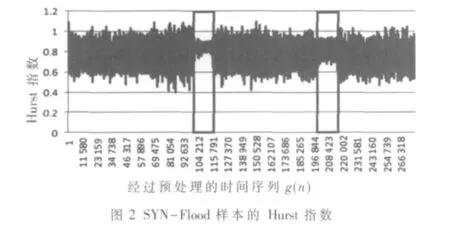
在框内的部分发生DDoS攻击(攻击发生于100 000 ms～117 998 ms及 200 000 ms～217 998 ms之间)，Hurst值在攻击发生时段明显趋于稳定。

经过方差处理后，在低流量背景情况下，Hurst指数方差值明显趋于0，比较容易检测出攻击。但是在高流量背景下（后一个框），攻击时Hurst方差值同正常流量的Hurst方差值大小并无明显区别，只能从趋势和前后节点数据关联性上看出一定特性。

用式(8)方法对Hurst指数进行方差和均值处理后，如图3、图4所示。从图中可以看出当DDoS攻击发生时，Hurst指数方差均值处于所设的阈值之下。

定义 1：误报率 σ，攻击发生的次数为 T，误报攻击的次数为t。误报率为误报攻击的次数与实际攻击发生次数的比值，即

定义2：检测延迟T，即攻击被检测出的时间与攻击发生时间之间的延迟。

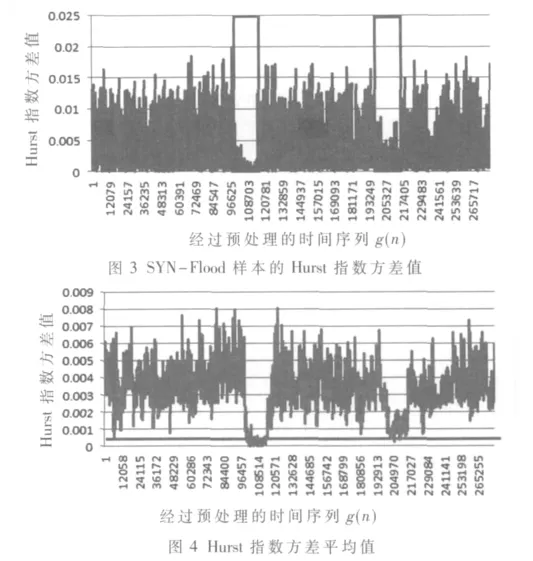
从实验结果可以得出,在利用BJUT-10流量模型进行异常检测时,当攻击流量达到背景流量36.90%时,攻击被检测出来，但检测完整性较差，仅为2.10%，检测延迟91.28 s。

当攻击增强而背景流量不变时，攻击的检测率提高，攻击检测完整性也相应提高；当攻击流量占到总流量91.36%时,检测率达到100%,检测完整性达到75.18%，检测延迟为26.1 s。

当攻击强度不变，背景流量发生变化时，在大流量背景下,检测的完整性较小流量背景下攻击的检测完整性和检测率差距较大，检测延迟明显降低。

4 与典型算法对比

为了验证本文算法的性能，采用相同的实验数据与典型检测方法进行了对比测试。

4.1 Holder指数检测法

本文重现了参考文献[6]中的Holder指数计算方法，并将关键实验参数设置为λ=0.9,s=10。

4.2 传统Hurst指数检测法

根据参考文献[6-7]中的 Hurst指数检测法，因Hurst指数检测法只适用于大尺度的网络模型，即时间敏感度大于1s的网络模型，因此本文采用BJUT-1000流量进行模拟检测。采用db(3)小波分解，小波分解层数为j=10，小波移动尺度 k=1，时间区间n=10。

4.3 性能比较

本文模拟的DDoS攻击包含了30 s攻击速率上升的过程，因此检测延迟在一定程度上反应了检测算法对攻击发生初期（0 s～30 s）的检测能力。

从图5可以看出本文方法在检测延迟上同Holder指数检测法性能相当。从算法误报率上看，本文方法误报率较Holder指数检测法有明显改善。因而本文方法在检测率和检测完整性上优于其他两种检测算法。如图6所示。

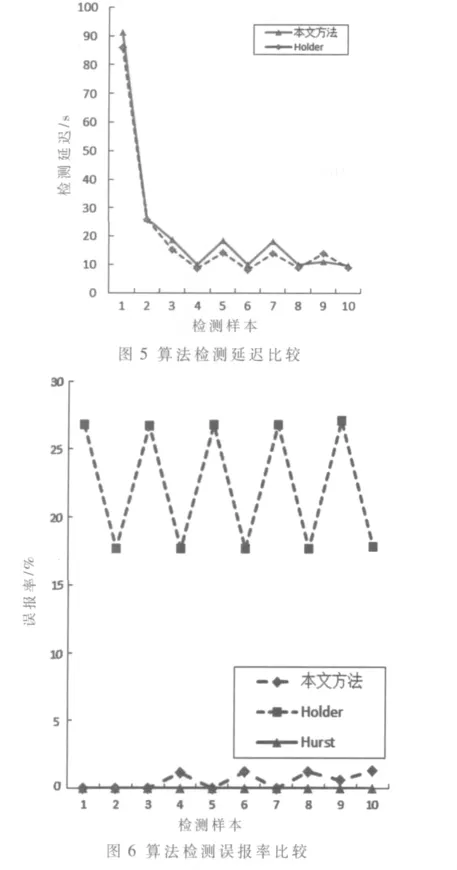
本文提出了一种基于多分形模型数据预处理的异常检测方法。利用小波分解的方法对网络流量进行分析。通过增加数据间相关性使得短相关的流量数据具备一定的长相关特性，而长相关数据的特性更加明显。同时使用Hurst指数方差平均值对攻击流量进行检测。相比于现有的实时检测算法,其误报率明显降低，并保持较低的检测延迟，提高了检测率和检测完整性。

参考文献

[1]JOSEPH L H,FAN Z,PEIWEZ S.Characterizing normal operation of a Web Server:application to workload forecasting and problem detection[C].Proceedings of the Computer Measurement Grouy,1998.

[2]THOTTAN M,JI C Y.Statistical detection of enterprise network problem[J].Journal of Network and Systems Management,1999,7(1):27-45.

[3]曹敏,程东年,张建辉,等.基于自适应阈值的网络流量异常检测算法[J].计算机工程,2009,35(19):164-167.

[4]ABRY P,VEITCH D,Wavelet analysis of long-range dependence traffic[J].IEEE Trans on Information Theory,1998,44(1):2-15.

[5]任义龙,刘渊,一种基于Holder指数的DDoS攻击检测方法[J].计算机应用研究,2011,28(2):724-727.

[6]任义龙,刘渊.一种基于小波分析的DDoS攻击检测方法[J/OL].[2011-09-29].http://www.cnki.net/kcms/detail/11.2127.tp.20110929.1037.054.html.

[7]李金明,王汝传.基于VTP方法的 DDoS攻击实时监测技术研究[J].电子学报,2007,35(4):791-796.

[8]胡俊,谭献海,覃宇飞.基于小波技术的网络流量分析与刻画[J].计算机应用,2007,27(11):2659-2665.

[9]任勋益,王汝传,祁正华.消失矩对小波分析求解自相似参数Hurst的影响研究[J],电子与信息学报,2007,29(9):2257-2261.

[10]任勋益,王汝传,王海艳.基于自相似检测DDoS攻击的小波分析方法[J].通信学报,2006,27(5):6-11.

[11]李永利,刘贵忠,王海军,等.自相似数据流的 Hurst指数小波求解法分析[J].电子与信息学报,2003,25(1):100-105.