基于B2DPCA和极端学习机的人脸识别

赵永卿，安建成

(太原理工大学计算机科学与技术学院，山西 太原 030024)

一个完整的人脸自动识别系统必须能可靠地完成人脸检测、特征提取和人脸识别。在此之前，一些研究人员使用了局部面部特征提取和分类来达到理想目标。自动人脸识别系统分为基于部件识别和基于面部识别［1］。可靠的面部特征提取是一个极其复杂的任务，因为人脸当大小和形状发生微小的变化时将会引起提取的特征发生变化。因此，研究人员提出把人脸看作二维强度模式的基于面部识别系统，并且通过检测和匹配其统计特性，将该系统实现，本文主要介绍基于面部识别。

Kirby［2］等人利用主成分分析法(Principal Component Analysis，PCA)把人脸描述成加权特征向量的线性组合，基于PCA的人脸识别系统有辨别能力差和计算量过大的缺点，J.Lu［3］等人为了改进人脸识别，提出利用线性判别分析法(Linear Discriminant Analysis，LDA)使类间散布矩阵和类内散布矩阵的比例达到最大值。J.M.Fellus［4］提出EP(Evolutionary Pursuit)法和弹性束图匹配法(Elastic Bunch Graph Matching，EBGH)以期产生最优轴投影。为了改善针对高维图像的人脸识别系统的性能，近些年研究的基于曲波变换的人脸识别方法有基于曲波变换的PCA法［5］、基于曲波变换的 LDA 法［6］和基于曲波变换的PCA+LDA法［7］。人脸识别算法有其自身局限性，比如对视点的变化、原型数量、分类速度有较大的敏感性。本文把曲波变换与双向二维主成分分析(Bidirectional Two Dimensional Principal Component Analysis，B2DPCA)和极端学习机(Extreme Learning Machine，ELM)结合起来消除以往方法中固有的缺陷。

1 曲波变换［8］

小波变换在传达准确的时间和空间信息上是一个显著的多分辨率分析工具，但小波变换也存在很多问题，针对这些问题，Candes和Donoho在1999年提出了曲波变换理论［9］，并构造了曲波的紧框架，对于具有光滑奇异性曲线的目标函数，曲波提供了稳定的、高效的和近乎最优的表示。曲波变换直接以边缘为基本表示元素，曲波变换是各向异性的，具有很强的方向性，非常有利于图像边缘的高效表示。它符合生理学研究所指出的“最优”的图像表示方法应具有的特征。

第一代曲波变换理论由脊波理论衍生而来。曲波变换和小波变换相同之处是都是多尺度变换，以刻度和空间位置参数为构成基础。但曲波变换有方向参数，曲波金字塔包含一种方向特征的基本原理。此外曲波变换基于各向异性尺度法则。

第二代曲波与第一代曲波在构造上已经完全不同，第一代曲波的构造思想是通过足够小的分块将曲线近似地当作每个分块中的直线来看待，然后利用局部的脊波分析其特性。而第二代曲波和脊波理论并没有关系，实现过程也不需要用到脊波。本文中主要利用曲波变换分解图像。

2 双向二维主成分分析法(B2DPCA)

Karhunen-Loeve展开式，又被称作主成分分析法(PCA)，是一种被广泛地应用在模式识别和压缩的数据表示技术。Yang［10］等人提出了2DPCA图像表示法，与PCA不同，2DPCA是基于二维矩阵而不是一维向量。因此，图像的矩阵在进行特征提取前不需要矢量化，而是使用原始图像矩阵直接计算图像协方差矩阵。

设X表示一个q维单位化列向量，2DPCA的思想是将p×q图像的矩阵A经线性变换Y=AX直接投影到X上，得到一个A的投影特征向量Y。可以用投影样本的总体散布情况来衡量投影向量X对样本的识别能力。投影样本的总体散布可用投影特征向量的协方差矩阵的迹进行描述。这样，可采用以下判定准则

式中:SX表示训练样本的投影特征向量的协方差矩阵，tr(SX)表示SX的迹。找出上式中判定准则的最大值的物理意义是找到一个使所有样本都能被涉及到的投影方向X，以使这些投影样本的总体散布被最大化。协方差矩阵SX可以表示为

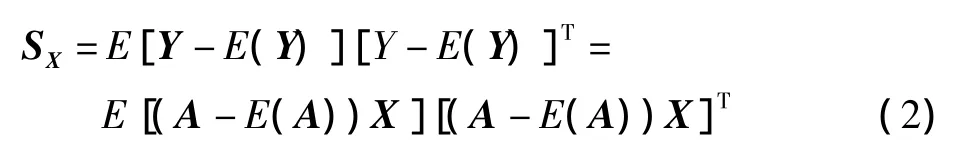
所以

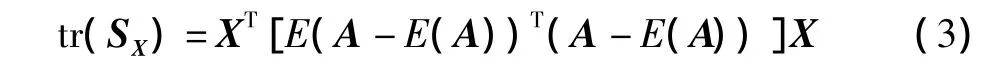
定义一个图像的协方差矩阵Gt

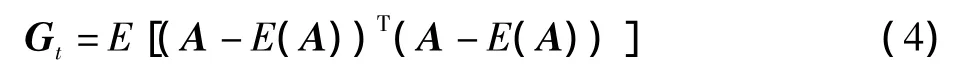
从定义容易证明Gt是一个非负的q×q矩阵。可使用训练图像样本直接计算Gt。假定共有M个训练图像样本，第α个训练图像样本用一个p×q矩阵Aα表示(α=1，2，…，M)，所有训练图像样本的平均图像用A表示。则Gt可由下式计算得到

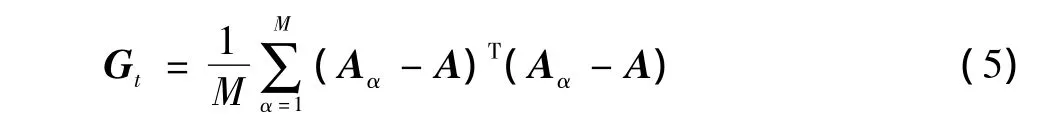
则有

使判定准则J(X)取最大值的线性向量Xopt称作最佳投影轴，一般情况下，只有一个最佳投影轴是不够的，通常需要选择满足正交条件和使判定准则J(X)取最大值的一簇投影轴 X1，X2，…，XM，实际上，最佳投影轴是 Gt对应于前M个最大本征值的正交本征向量。

基于2DPCA识别的局限性使它的可操作性只能沿着行方向，Zhang和Zhou［11］在基于假设训练图像零均值的基础上提出(2D)2PCA方法。因此，可以用行/列图像矢量的外积计算图像的协方差矩阵。利用式(5)计算出GtRow和GtCol，首先按照Aα和A的行向量计算，接着对其列向量用相同方法。对GtRow和GtCol的最佳投影轴进行取值分别记作X1opt和Z1opt，值得一提的是Gt和GtRow都是基于行计算的，因此它们的最佳投影轴Xopt和X1opt是相似的，通过变换把Aα表示成。

为了保证行列关系和生成区别特征集，降维算法沿行列是独立完成的，本文方法是利用最佳投影轴生成图像协方差矩阵［11］，并对其进一步优化。一旦最佳投影轴把Xoptα计算出来，图像的矩阵Aα沿其列向量降维，利用式(7)得到图像集Aβ，把新生成的图像集看作一个新的数据库，计算得出新的图像协方差矩阵Gtβ和新的最佳投影轴Xoptβ。最后，通过式(8左乘Aβ得到输出矩阵AΘ

Kong［12］等人将 2DPCA 进行改进，提出了 B2DPCA(Binary Two Dimensional Principal Component Analysis)算法来降维。本文在算法一中简单介绍了此算法主要步骤。

算法一:B2DPCA算法

INPUT:输入图像的矩阵 AN×N，N∈Z+。

OUTPUT:输出M×M矩阵AΘ，N∈Z+。

1)利用式(5)计算Aα图像的协方差矩阵Gtα;

2)计算 J(X)=XTGtαX;

3)最佳投影轴 Xoptα={X1，X2，…，XM}，Xi表示正交向量;

4)沿列降维得到 Aβ=AαXoptα;

5)计算Aβ的图像协方差矩阵Gtβ;

6)同步骤(3)计算 Xoptβ;

7)通过式(8)进行行降维。

3 极端学习机

传统前馈神经网络多采用梯度下降算法调整权值，缺点是学习速度较慢、泛化性能差，为了解决这些缺陷，Huang［13］等人提出了极端学习机算法(Extreme Learning Machine，ELM)，该算法对单隐层神经网络的输入权值和隐层节点偏移量进行随机赋值，并且只通过一步计算即可解析求出网络输出权值，如图1所示。

考虑到N 个不同样本集(xi，ti)，其中 xi=［xi1，xi2，…，xin］T∈Rn，ti=［ti1，ti2，…，tim］T∈Rm，可以把含有 L 个隐节点和一个激活函数ξ(x)的ELM建模为

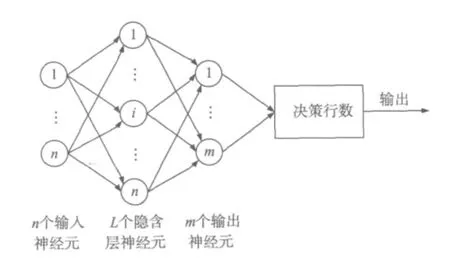
图1 极端学习机分类器结构

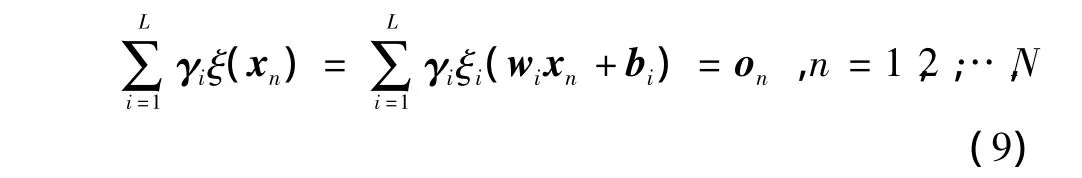
式中:wi=［wi1，wi2，…，win］表示输入;γi=［γi1，γi2，…，γin］表示隐含层权值向量;bi是隐节点偏移量。极端学习机以最小的误差近似于N个样本如下

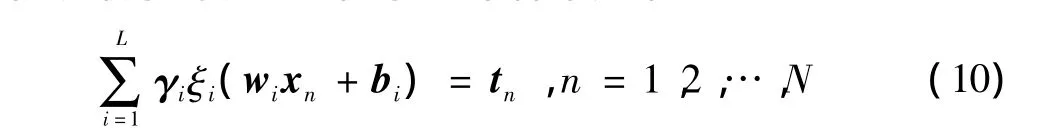
式(10)也可以表示成 δγ = τ ，δ =(w1，w2，…，wL，b1，b2，…，bL，x1，x2，…，xN)，这样 δ 的第 i列就表示输入为x1，x2，…，xN的第i层隐节点的输出。如果激活函数ξ(x)是无穷可微的，事实证明隐节点数L≪N，极端学习机的训练需要把误差函数E最小化

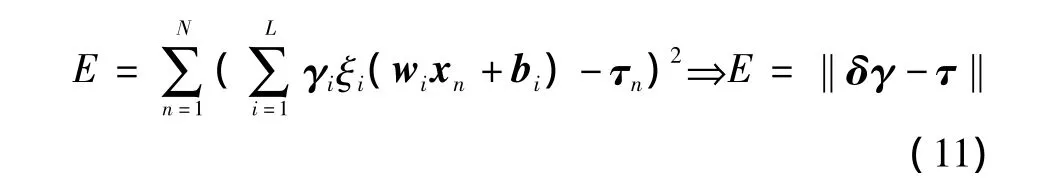
经典神经网络δ是利用梯度下降算法调整的，在学习效率为ρ情况下，把输入权值wi，隐含层权值γi，隐节点偏移量bi进行迭代调整。ρ值过小将会使学习算法收敛速度过慢，而ρ值过大又会导致不稳定。为了解决这一问题，ELM采用了极小范数最小二乘法。网络的输入权值和偏移量可直接随机赋值而不必采用梯度下降算法迭代调整，而δγ=τ的最小二乘法可以简化这个问题。隐含层输出矩阵δ是一个非方阵，范数最小二乘法可以归纳为γ=δ*τ，其中δ*表示δ的广义逆矩阵。因为ELM表示一个线性系统的最小二乘法，所以可以得到一个无限小的训练误差，公式为

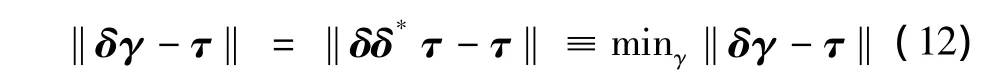
4 本文提出的人脸识别算法

本文方法是基于曲波变换的图像分解和使用降维后的系数来识别的，利用B2DPCA得的特征集来训练和测试ELM分类器，算法示意图如图2所示。

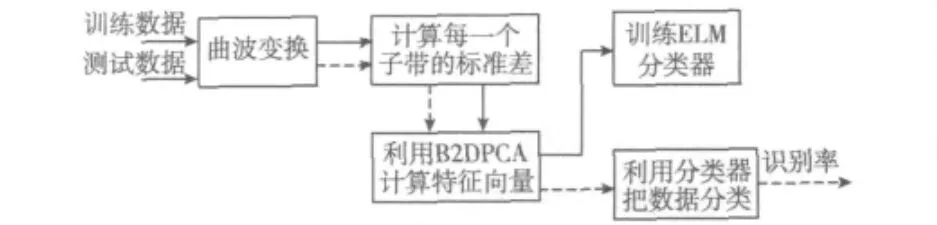
图2 本文人脸识别算法示意图

数据库中每个图像大小减小一倍转换成灰度图像，每个图像数据库随机分为训练集和测试集，这样每个目标图像有40%～45%当作原型，剩下的图像用在测试阶段。曲波变换用来生成初始特征向量，因为它不仅在存有奇异点的高维矩阵中显示优越的性能，而且能以最小的噪声影响增强高频成分的定位。首先把输入图像尺寸重置，因为当全局信息在同一层次的时候，类似图像尺寸支持曲波特征向量的生成。此外，所有数据库中图像的曲波分解是在3个尺度8个角方向下计算的，因此，长生25个不同的子带。

计算出每个子带的标准差，选取标准差最大的子带作为初始特征向量，尺寸为U×V，其中U×V≪R×C，其中R×C是输入图像尺寸。与T.Mandal［14］等人选择2个子带相比，本文仅仅选择了1个子带，那是因为2个标准差不同子带的区别是十分明显的，所有被测试数据库标准差都有显著差别。该方法的基础是选择最大标准差的子带，这在降维时可以最大限度地节约计算成本。

B2DPCA是用来生成独特特征集的，并且使整体框架计算复杂度最简化。2DPCA法以一个单一的协方差矩阵分别沿行和列对图像降维，然而本文提出的方法是沿与坐标轴无关的正交方向降维。通过初始特征矩阵的初次降维提取中间特征，即沿其列选取曲波子带。然后沿中间特征的行对其进行降维以得到最终特征集，每个特征集尺寸为U′×C′，其中U′×C′≪U ×V。本文经过改进的方法能保存临近像素点之间的关键邻域信息，并且能生成区别性的特征。对于每一个数据集，随机选择其中降维后的曲波特征集用于ELM的训练，而同一个数据集中剩余特征集用来判断框架的可分离性。

5 实验结果与分析

利用ORL和GTech人脸数据库，用本文提出的方法进行了大量实验。所有图像的维数降低一倍，并从RGB转换成灰度图像。在所有数据库中，每个目标图像的40%～45%作为原型，而剩下的用作测试目的。利用曲波变换在3个尺度8个角方向下训练和测试图像，先利用B2PCA得到降维后的近似曲波系数，接着利用ELM进行矢量化、训练和测试。针对每个数据库，每个实验做100次，保留平均结果。为了简单起见，接下来的实验把本文方法的结果和基于曲波的PCA+LAD方法［14］得到的结果相比较。

通过ORL数据库和GTech数据库，用不同数目主成分实验得到的平均识别率和基于曲波的PCA+LAD法相比较得到的结果如表1所示。以下实验数据可以看出，本文提出的方法识别准确率高于基于PCA+LAD的方法。本文的方法对于ORL数据库和GTech数据库识别率的提高是明显的，并且适用于具有挑战性的数据库(视点在各个方向)。值得一提的是，增加主成分数量不是提高识别率的必要条件，利用人脸识别的局部信息也有可能产生更好的结果。本文提出的方法和其他人脸识别算法相比除了提高了识别率之外，另一个优点是原型的数量对于识别率影响非常小。ORL数据库中原型数量分别占30%，40%，60%，70%时的识别率如图3所示(y轴表示平均识别率，x轴表示主成分的数量)。

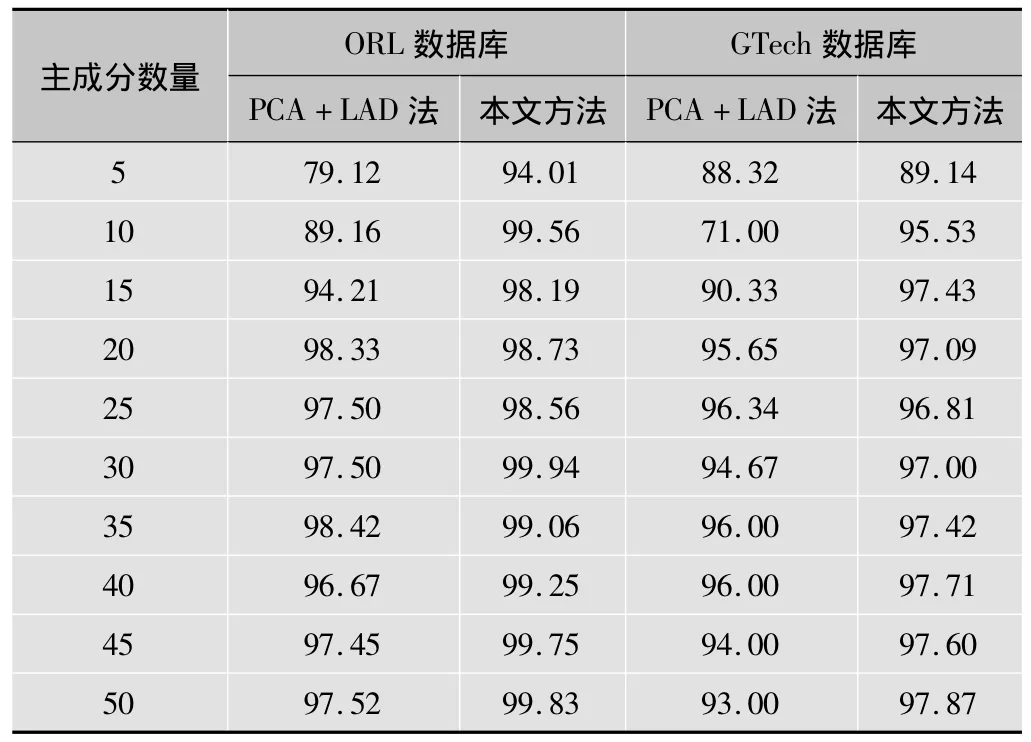
表1 ORL和GTech人脸数据库平均识别率 %

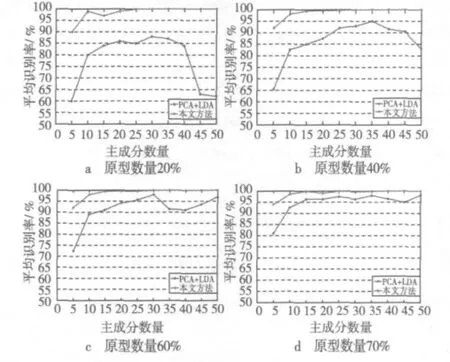
图3 原型数量占不同比例时的平均识别率

6 结论

本文基于曲波特征空间提出了一种高效的人脸识别技术，曲波变换是用来实现高维稀疏性的，利用B2DPCA对稀疏特征降维得到不同特征集。最后把这些特征集作为ELM的输入来分析学习最优模型。实验证明本文提出的方法不仅比现存的方法识别准确率有所提高，而且在用以训练的原型数量上具有独立性。在将来，希望能把局部特征和基于曲波分解的全局信息结合起来应用到识别精度和分类速度上。

［1］闫娟，程武山，孙鑫.人脸识别的技术研究与发展概况［J］.电视技术，2006，30(12):67-69.

［2］KIRBY M，SIROVICH L.Application of the Karhunen– Loeve procedure for the characterization of human faces［J］.IEEE Trans.Pattern A-nalysis and Machine Intelligence，1990，12(1):103-108.

［3］LU J，PLATANIOTIS K N，VENETSANOPOULOS A N.Face recognition using LDA-based algorithms［J］.IEEE Trans.Neural Networks，2003，14(1):195-200.

［4］WISKOTT L，FELLUS J M，KRUGER N，et al.Face recognition by elastic bunch graph matching［J］.IEEE Trans.Pattern Analysis and Machine Intelligence，1997，19(7):775-779.

［5］FENG G C，YUEN P C，DAI D Q.Human face recognition using PCA on wavelet subband［J］.Journal of Electronic Imaging，2000，9(2):226-233.

［6］CHIEN J T，WU C C.Discriminant waveletfaces and nearest feature classifiers for face recognition［J］.IEEE Trans.Pattern Analysis and Machine Intelligence，2004，24(2):1644-1649.

［7］MANDAL T，WU Q M，YUAN Y.Curvelet based face recognition via dimension reduction［J］.Elsevier Signal Processing，2009，89(3):2345-2353.

［8］吴春颖.浅谈曲波变换的应用［J］.福建电脑，2011(10):79-80.

［9］CANDES E J，DEMANET L，DONOHO D L，et al.Fast discrete curvelet trans-forms［J］.Multiscale Modeling and Simulation，2006，5(3):861-899.

［10］YANG L，ZHANG D，FRANGI A F，et al.Two-dimensional PCA:a new approach to appearance based face representation and recognition［J］.IEEE Trans.Pattern Analysis and Machine Intelligence，2004，26(1):131-137.

［11］ZHANG D，ZHOU Z H.(2D)2PCA:two-directional two-dimensional PCA for efficient face representation and recognition［J］.Elsevier Neurocomputing，2005，69(1):224-231.

［12］KONG H，WANG L，TEOH E K，et al.Generalized 2D principal component analysis for face image representation and recognition［J］.Neural Networks，2005，18(5-6):589-594.

［13］HUANG G Q，ZHU Q，SIEW C.Extreme learning machine:theory and applications［J］.Elsevier Neurocomputing，2006，70(1-3):489-501.

［14］MANDAL T，WU Q M，YUAN Y.Curvelet based face recognition via dimension reduction［J］.Elsevier Signal Processing，2009，89(3):2345-2353.