结合粒子群算法的一类双层纺织材料厚度设计反问题
周 远, 徐映红, 徐定华
(浙江理工大学 理学院,浙江 杭州 310018)
结合粒子群算法的一类双层纺织材料厚度设计反问题
周 远, 徐映红, 徐定华
(浙江理工大学 理学院,浙江 杭州 310018)
为给纺织材料的功能性设计提供理论支持和科学解释,基于低温环境下纺织材料热湿传递稳态模型,研究一类双层纺织材料厚度设计反问题。首先给出一个双层纺织材料热湿传递稳态模型及相应的边界条件,该模型是关于温度和湿度的耦合常微分方程组,通过解耦可化为两点初边值问题,并采用有限差分法求解;然后根据服装热湿舒适性要求,将纺织材料内层厚度看成一个未知量,提出了一类双层纺织材料厚度设计反问题,并将该反问题归结为一个具有最小二乘解的优化问题;最后采用粒子群算法求解该优化问题。结果表明,双层纺织材料厚度设计反问题是合理的,粒子群算法能有效地解决该反问题,该算法具有鲁棒性。
纺织材料; 厚度设计; 双层热湿传递模型; 反问题; 粒子群算法
从20世纪30年代开始,世界各国的学者对纺织服装材料热湿传递问题进行了大量研究,主要集中在数学模型的建立与分析、数值模拟上。Farnworth[1]给出了多层纺织材料间的热湿传递模型,模型包含了热传导、辐射热和扩散引起的湿传递,忽略了对流引起的热湿传递。Li等[2]研究了人体、环境和织物之间动态的热湿耦合模型。Fan等[3]研究了包含吸附和凝结在内的多孔织物的耦合动态热湿传递模型。Fan等[4]研究了在低温下内外层由一种新型的出汗防护热板覆盖的多孔纤维材料的温度和水分分布。
纺织材料热湿传递研究主要解决数学模型的合理提出,边界值与初始条件如何给出,并通过数值模拟来研究纺织材料的热湿传递特性。纺织材料热湿传递模型因为材料的极薄性、多层性、多孔性并同时伴随热力过程,如凝结、汽化、湿传递等特点变得十分复杂,其模型往往是耦合的非线性方程,因此对纺织材料热湿传递正问题的合理性研究显得非常重要。在已有研究工作中这些模型的合理性没有通过数学理论来验证,甚至有些模型解的存在性、唯一性和连续依赖性都没有进行合理分析,所进行的数值模拟也是依据不足。因此有必要从数学上研究纺织材料热湿传递问题以及相应的功能设计反问题。
服装舒适性包含3个潜在的独立感觉因子:热湿舒适因子、触觉舒适因子和压力舒适因子[5]。热湿舒适性作为服装总体舒适性的主要部分对服装舒适性有积极影响。基于热湿传递特征的功能性纺织材料设计是根据人体热湿舒适性要求,决定材料的类型、厚度或组织结构等,这属于一类数学物理的反问题。通过反问题的理论和方法研究纺织材料设计,可为纺织材料设计试验和产品研发提供理论依据。国内外关于该方面的研究结果很少,徐定华等[6-7]研究了一类单层纺织材料类型设计反问题和一类双层纺织材料厚度设计反问题。
本文主要研究了一类双层纺织材料厚度设计反问题,并使用粒子群算法进行数值求解。在文献[7]的基础上,主要做了以下2方面的改进:减少为5个边界条件,使边界条件的提法更为合理;2)使用粒子群算法求解,该方法是一种随机性算法,不依赖于初始值的选取,在参数值选取适当的情况下能收敛到问题的全局最优解。
1 双层纺织材料厚度设计正问题
首先,提出双层纺织材料厚度设计的正问题及其数值求解过程。
1.1 热湿传递模型
假设衣服由2层不同材料组成,织物内、外层厚度分别为L1、L2,总厚度为L=L1+L2。织物内层与人体之间的空气构成一个微气候区,外层暴露在稳定的外部环境中。
对于服装内层有如下一维稳态热湿传递模型:
(1)
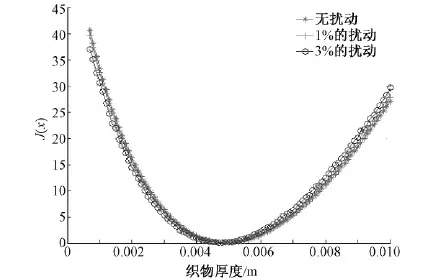
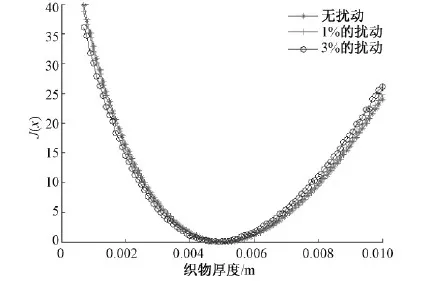
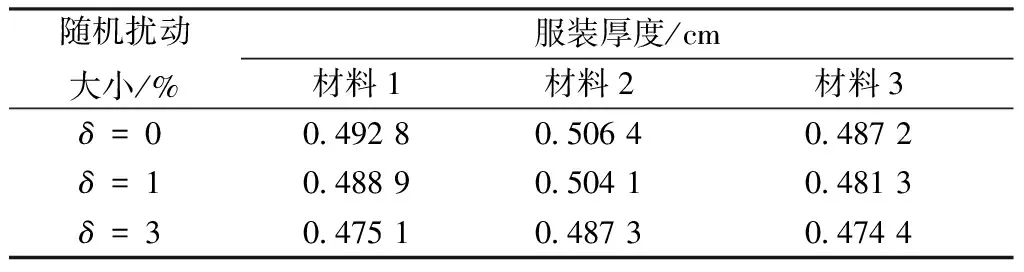
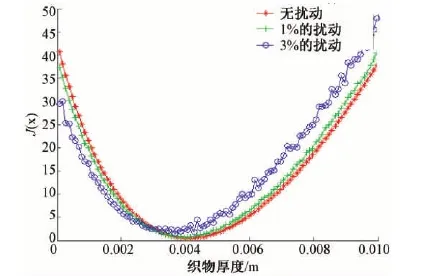
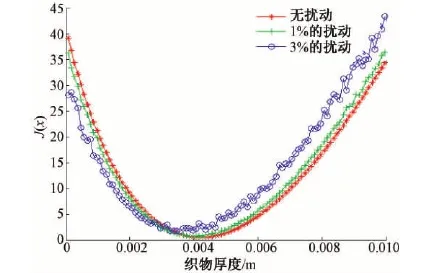
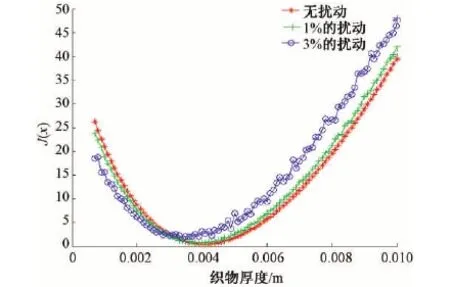
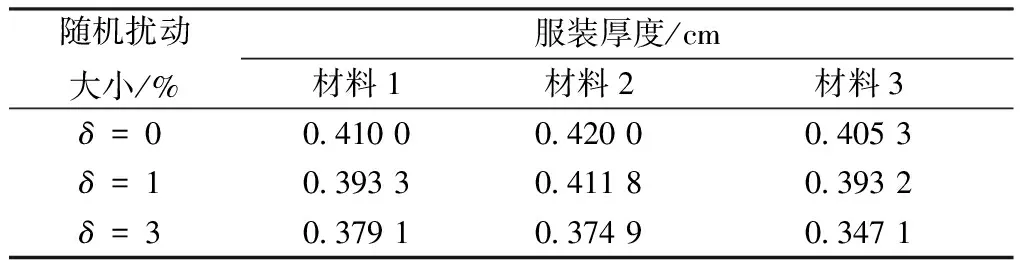
式中0 T(0)=T0 (2) 对于织物外层有: (3) 式中L1 (4) 上述模型建立在以下假设条件下:1)纺织品空隙形态结构采用“平行圆柱孔”模型;2)纺织品各向同性;3)系统各边界处的热湿传递都是连续;4)因为湿度和水含量的变化而导致纺织材料的体积变化可忽略不计。已知常微分方程组(1)、(3)以及边界条件(2)、(4)求纺织物内部的温度和湿度分布为双层纺织材料热湿传递正问题。本文与文献[7]相比,主要减少了织物内层与外层之间水蒸气质量通量这个边界条件。 1.2 热湿传递正问题的数值求解 利用有限差分法对正问题进行数值求解。令 对外层织物,将方程组(3)解耦,得到如下2点边值问题: (5) 其中: (6) 当i=N时,有: (7) 对于i=0,1,2,…,N-1,还有 (8) (9) 对内层织物,对方程(1)进行解耦,可以得到: (10) 式中: pv(x)= 关于服装热湿舒适性,衣服内侧至皮肤表面间服装微气候区的最舒适条件可表述为温度、湿度和气流速度的组合:温度为(32±1) ℃,相对湿度为50%±10%,气流速度为(0.25±0.15)m/s[8]。 下面考虑双层纺织材料厚度设计反问题,给定环境温度-湿度组合为 双层织物的材料结构和类型以及外层织物厚度,根据服装的热湿舒适性要求,决定内层织物的厚度,其中Tmin、Tmax分别为某地某时间段的最低日平均温度、最高日平均温度,RHmin、RHmax分别表示某地某时间段的最低日平均相对湿度、最高日平均相对湿度。 该反问题可转化为一个最小二乘问题。将环境温度-湿度的组合离散为 (Ti,RHj)(i=1,2,…,n;j=1,2,…,m) 满足上式的x*称为双层厚度设计反问题的最小二乘解。 3.1 反问题的算法设计 上述最小二乘问题属于单变量最优问题,但计算出RHi,j,0(x)的导数非常困难,故不使用导数的算法进行求解。文献[7]采用直接搜索法Hooke-Jevees算法进行求解,该算法是一种局部收敛方法,依赖于初始值的选取,而本文使用粒子群算法[9-10]求解,该方法是一种随机性算法,不依赖于初始值的选择,能收敛到全局最优解。 (11) (12) 式中:i=1,2,…,M;d=1,2,…,D;k为迭代次数;ω为惯性因子;r1和r2为[0,1]之间的随机数;c1和c2为学习因子。粒子群算法的计算步骤如下: 第1步:选择阈值ε和最大迭代次数Nmax;每个粒子的初始位置和初始速度分别为: 3.2 数值实例 下面将给出几个数值实验,以此来检验上述双层纺织材料厚度设计反问题提法的合理性和算法的有效性。 考察服装材料在2组不同温度和湿度组合下的厚度反演结果。材料的类型和结构参数见文献[7],3种材料类型分别为,材料1:外层羊毛,内层涤纶;材料2:外层涤纶,内层羊毛;材料3:外层羊毛,内层聚丙烯纤维。 情况1:当环境温度为[-15 ℃,0 ℃],相对湿度为[40%,90%]时,图1、2、3分别给出了对应3种不同类型材料的函数J(x)的图像。 图1 情况1下材料1的J(x)图像Fig.1 Figures of J(x) with material 1 in case 1 图2 情况1下材料2的J(x)图像Fig.2 Figures of J(x) with material 2 in case 1 图3 情况1下材料3的J(x)图像 Fig.3 Figures of J(x) with material 3 in case 1 情况2:当环境温度为[0 ℃,15 ℃],相对湿度为[30%,85%]时,图4、5、6分别对应3种不同类型材料的函数J(x)的图像。 由图1~6可知,3种材料在上述2组温度-湿度组合下都存在极值且唯一。表1、2给出了用粒子群算法分别计算出情况1和情况2下3种类型织物的厚度反演结果,粒子群算法计算结果与图形所示结果一致。 表1 情况1下3类服装的厚度设计的数值结果Tab.1 Numerical results of three kinds of textile materials in case 1 图4 情况2下材料1的J(x)图像Fig.4 Figures of J(x) with material 1 in case 2 图5 情况2下材料2的J(x)图像Fig.5 Figures of J(x) with material 2 in case 2 图6 情况2下材料3的J(x)图像Fig.6 Figures of J(x) with material 3 in case 2 随机扰动大小/%服装厚度/cm材料1材料2材料3δ=0041000420004053δ=1039330411803932δ=3037910374903471 服装热湿舒适性反问题的研究可为服装设计尤其是恶劣条件下的防护服装设计提供科学依据,以设计出更人性化的服装,可以在服装制作之前就对服装的舒适性和功能性进行全面预测,从而指导生产。 本文根据双层纺织材料的稳态热湿传递模型,提出双层纺织材料厚度设计反问题。采用有限差分法来求解相应的正问题,将反问题归结为最小二乘问题,并采用粒子群算法进行求解,获得了有效的数值结果。 1)双层纺织材料厚度设计反问题的提法是合理的,在类型给定的情况下,为纺织服装产品厚度设计提供理论支持和科学解释,以确保服装的热湿舒适性。 2)粒子群算法能够有效地解决双层纺织材料厚度设计反问题,获得最优解;粒子群算法具有全局收敛的,无初值依赖性。但是,在采用粒子群算法时,需要选择一个合适的速度控制,太大会错过最优值,太小又将导致搜索不充分。 3)粒子群算法对小扰动问题是稳定的,即当条件给与了一个微小扰动的时候,结果的变化很小。 FZXB [1] FARNWORTH B. A numerical model of the combined diffusion of heat and water vapor through clothing[J]. Textile Research Journal, 1986, 56(11): 653- 665. [2] LI Yi, HOLCOMBE B V. Mathematical simulation of heat and moisture transfer in a human-clothing-environment system [J]. Textile Research Journal. 1998, 68(6): 289-297. [3] FAN Jintu, LUO Zhongxuan, LI Yi. Heat and moisture with sorption and condensation in porous clothing assemblies and numerical simulation[J]. International Journal of Heat and Mass Transfer, 2000, 43: 2989-3000. [4] FAN Jintu, CHENG Xiaoyin, CHEN Yisong. An experimental investigation of moisture absorption and condensation in fibrous insulations under low temperature[J].Experimental Thermal and Fluid Science, 2003, 27(6):723-729. [5] 孟祥玲,张渭源. 服装压力舒适性的研究进展[J].纺织学报, 2006,27(7): 109-112. MENG Xiangling,ZHANG Weiyuan. Progress of study on pressure comfort of clothing[J].Journal of Textile Research, 2006,27(7): 109-112. [6] 徐定华,陈远波,程建新.低温环境下纺织材料类型设计反问题[J]. 纺织学报, 2011, 32(1): 6-11. XU Dinghua,CHEN Yuanbo,CHENG Jianxin. Inverse problem of textile material design at low temperature[J]. Journal of Textile Research, 2011, 32(1): 6-11. [7] XU Dinghua, CHENG Jianxin, CHEN Yuanbo, et al. An inverse problem of thickness design for bilayer textile materials under low temperature[J]. Journal of Physics: Conference Series, 2011, 290(1): 12-18. [8] 黄建华.服装的舒适性[M]. 北京: 科学出版社, 2008. HUANG Jianhua.Clothing Comfort [M].Beijing:Science Press,2008. [9] 纪震,廖惠连,吴青华.粒子群算法及应用[M].北京:科学出版社, 2009. JI Zhen,LIAO Huilian,WU Qinghua.Particle Swarm Algorithm and Its Application[M].Beijing: Science Press, 2009. [10] 徐定华,葛美宝.一类纺织材料热湿传递模型的数值解法[J].江西科学,2010,28(5):578-582. XU Dinghua, GE Meibao.A numerical method of a heat and moisture transfer model in textiles[J].Jiangxi Science,2010,28(5):578-582. Inverse problem of thickness design for bilayer textile materials combined with particle swarm algorithm ZHOU Yuan, XU Yinghong, XU Dinghua (SchoolofScience,ZhejiangSci-TechUniversity,Hangzhou,Zhejiang310018,China) This paper deals with an inverse problem of estimating bilayer textile fabric thickness based on a one-dimensional steady-state heat and moisture transfer model to provide theoretical support and scientific explanation for functional design for textile material. We first present a model of heat and moisture transfer for bilayer textile materials with boundary conditions, which is a coupled ordinary differential equation including temperature and humidity. We transform them into two two-point initial and boundary value problems by decoupling and solve them by finite difference method. According to the requirement of heat and moisture comfort of clothing, we then formulate this inverse heat and moisture transfer problem which estimates the thickness of inner layer fabric as an optimization problem with least square solution. Finally, we use particle swarm algorithm to solve this inverse problem. The results demonstrate that our inverse problem is quiet acceptable, and the particle swarm algorithm effectively solves this inverse problem, showing the proposed method is robust. textile material; thickness design; model of heat and moisture transfer for bilayer textile; inverse problem; particle swarm algorithm 0253- 9721(2013)06- 0040- 06 2012-06-10 2012-08-17 国家自然科学基金面上项目(NSFC11071221);浙江省自然科学基金青年基金项目(LQ12A01024) 周远(1989—),男,硕士生。主要研究方向为数学物理方程反问题、纺织材料设计的数理分析。徐映红,通信作者,E-mail:xyh7913@126.com。 TS 101.1 A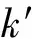
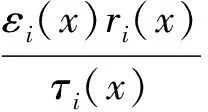
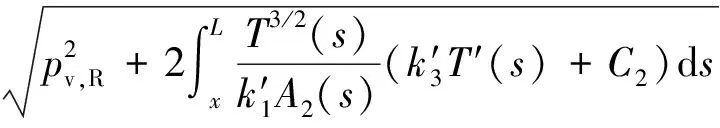
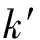
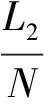
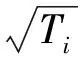
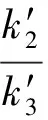
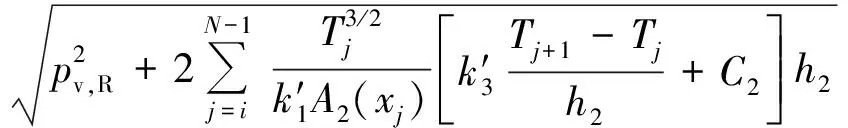
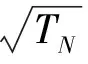
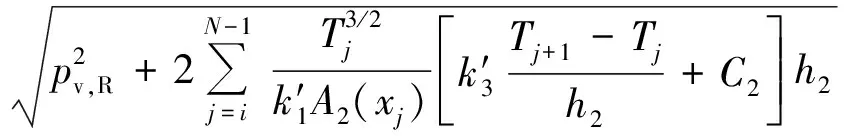
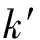
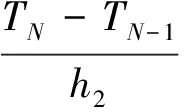
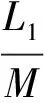
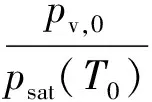
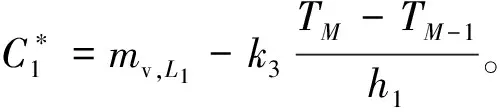
2 内层厚度设计反问题及其数学描述
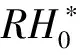
3 厚度设计反问题的数值求解
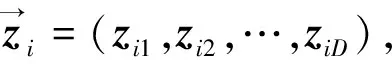
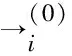
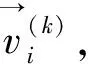
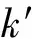
4 结 论

