自升式平台的自由振动计算方法研究

孙雪荣 程维杰

（中国船舶及海洋工程设计研究院 海洋工程部 上海200011）

0 引 言

自升式海洋平台主要由平台主体结构、桩腿、升降结构、钻井机构等组成；作为支撑平台站立和安全进行钻井作业要求的桩腿结构，因其自由振动的周期一般在 5～15 s［1］，尤其是现代自升式海洋平台日趋向更深水域发展，平台自由振动的周期与工作水域海浪周期遭遇的几率越来越大，平台的振动动态响应问题愈加显著；因此在工程设计的初始阶段快速和准确的预估平台的自由振动周期和动力效应显得尤为重要。

论文以某400 ft平台为基础，以直接简化计算［2］和有限元方法进行自升式海洋平台自由振动计算方法的探讨。文章对于理论上的振动计算方法不加以阐述，旨在探讨比较方便和快速有效的工程实用方法，达到前期设计阶段辅助平台总强度和桩腿设计的目的。

1 计算模型简介

论文中的计算模型选取平台处于风暴自存状态下的装载为计算状态，其环境载荷见表1。

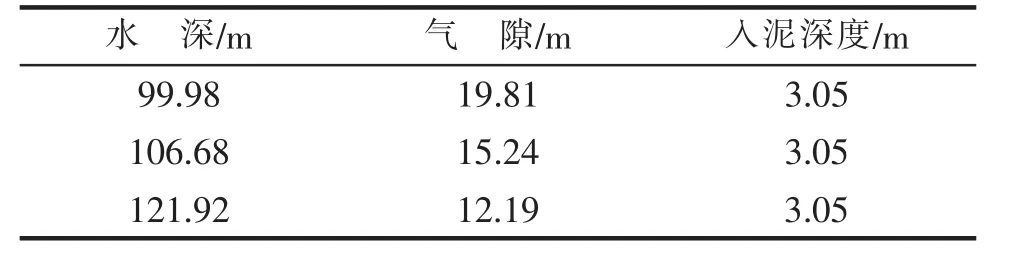
表1 风暴自存状态下的环境载荷

该平台的桩腿结构图参见图1和图2。

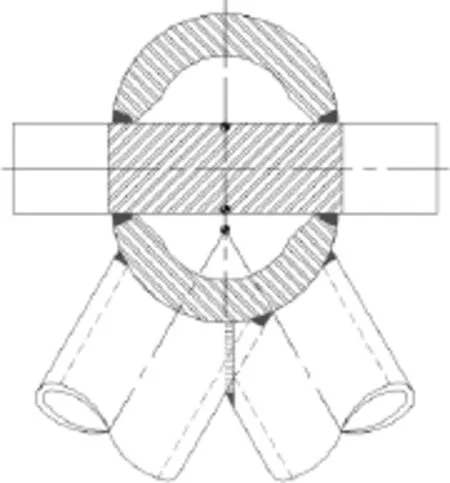
图1 桩腿剖面结构示意图

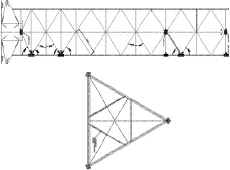
图2 桩腿结构示意图

2 直接简化计算

本节中自由振动直接简化计算方法参考自文献［2］中第7.3.5节，平台振动的一阶自然频率计算公式：。其中，各参数的详细含义可参见文献［2］中相应章节，本文仅列出典型参数的含义及计算：

Me为与单个桩腿相应的有效质量，

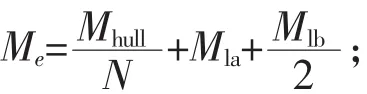
Mhull为主船体质量，包括最大可变载荷；

Mla为LOWER GUIDE之上的桩腿质量；

Mlb为LOWER GUIDE之下桩腿质量，含附连水质量；

Ke为单个桩腿的有效刚度。

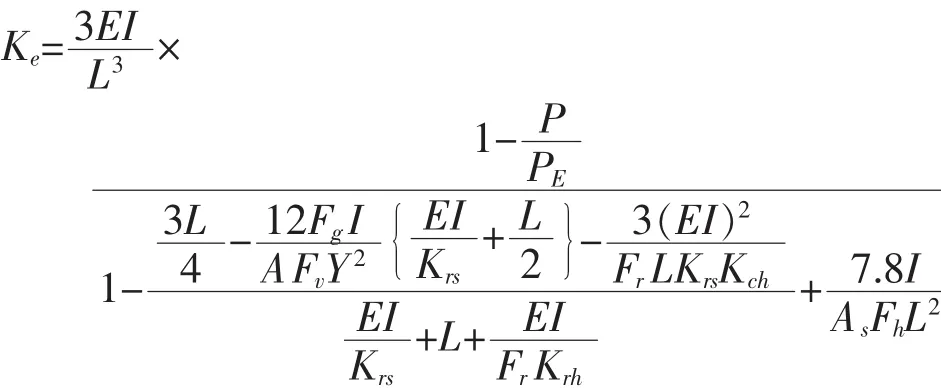
PE为单个桩腿的EULER屈曲载荷）；

Kvs、Krs、Khs分别为平台站立处的泥介质与桩靴作用的垂向刚度、扭转刚度与水平刚度；

Kvh、Krh、Khh分别为桩腿与船体连接处的垂向刚度、扭转刚度与水平刚度；

Fr为考虑主船体弯曲刚度的因子

Fv为考虑泥土垂向刚度和桩腿船体连接垂向刚度的因子，

Fh为考虑泥土横向刚度和桩腿船体连接横向刚度的因子，

至此，可以认为：

（1）泥面以下3 m处桩腿简支：Kvs=Khs=∞，Krs=0；

（2）主船体的升降机构室与桩腿的连接；Krh=∞，Kvh、Khh与升降机构室系固系统以及桩腿自身的垂向和水平刚度有关。

2.1 桩腿的附连水质量

桩腿具体几何参数见表2。

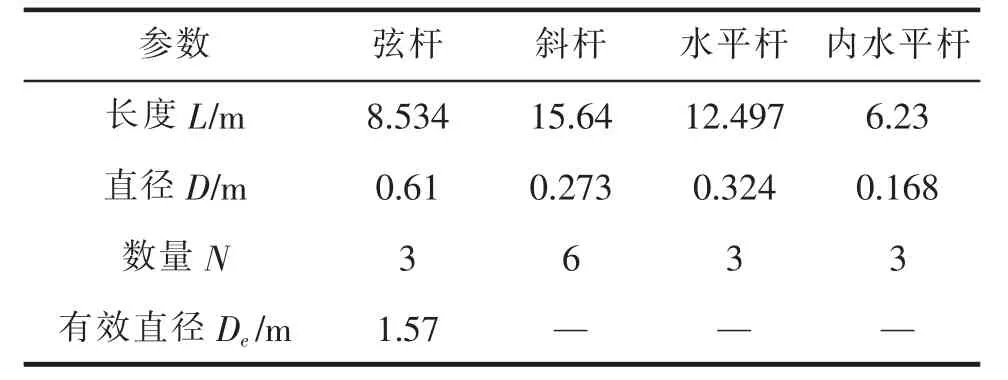
表2 桩腿截面几何参数

单位长度的附连水质量由公式Mlb-f=Aeρ（CMe-1）计算得出。

式中：ρ=1.025 t/m3，为海水密度；

CMe=2.0，为惯性力系数；

De为桩腿等效直径［2］，单个桩腿总的附连水质量由公式 Mlb-ft=Aeρ（CMe-1）Lwater计算得出，依次为：197.8 t（99.98 m水深）、211 t（106.68 m 水深）、241.2 t（121.92 m 水深）。

2.2 单个桩腿的有效质量

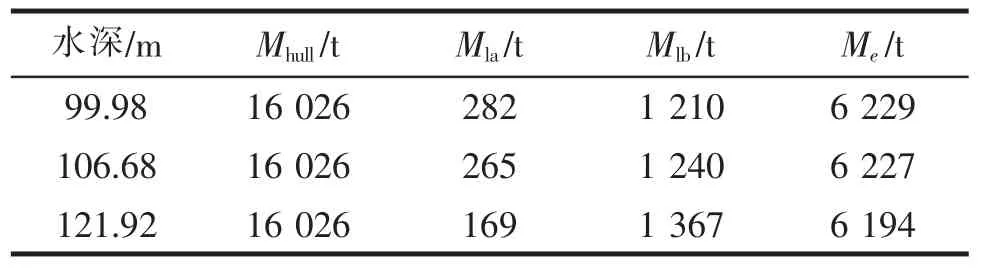
表3 桩腿有效质量计算

2.3 桩腿截面的各参数

桩腿弦杆截面属性如图3所示。

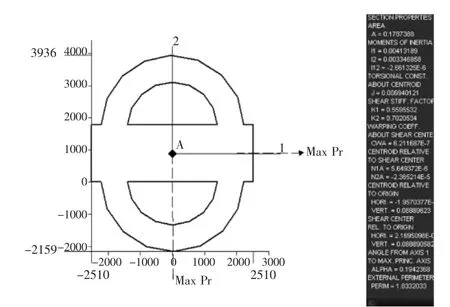
图3 桩腿弦杆截面属性（含10%齿条）

依据文献［1］附录1中相应内容进行，其桩腿截面各参数属性及计算过程如下：

截面边长H/m 13.11

斜杆截面面积Ad/m20.017

水平杆截面面积Av/m20.027

弦杆截面面积Ac/m20.179

等效剪切面面积Aqi/m20.034

桩腿截面积A=3Aci/m20.536

桩腿剪切面积Aqy=Aqz=1.5·Aqi0.051

平面惯性矩 Iy=Iz=0.5·Aci·h215.352

扭转惯性矩 It=0.25·Aqi·h21.448

2.4 桩腿与船体连接处刚度

桩腿与船体连接处刚度计算流程如下：

弹性模量E 206 000 MN/m2

绑扎系统结构长度L13.26 m

rack chock截面积A_CHOCK0.124 6

rack chock长度L_CHOCK1.727

绑扎系统刚度Kvfix_system/chord

14 866 mn/m/chord EA_CHOCK/L_CHOCK

垂向连接有效刚度Kv_effective

19 255 MN/m 1/（1/（3×Kfix）+L/（EA））

BAY间距 8.1 m

绑扎系统有效结构深度 858 mm

绑扎系统有效结构宽度 767 mm

绑扎系统有效结构惯性矩Ic0.012 m4

绑扎系统有效结构长度Lc3.26 m

水平杆水平有效刚度Khch_hori437 EA_hor/L_hor

支杆水平有效刚度Khch_br

446 mn/m 2×E×Abr/Lbr

弦杆水平有效刚度Khch_chord

251mn/m 192×E×Ichord/Lchord3

上导向结构处的有效水平刚度Khch_guide

140 mn/m （2×E×Ic）/（Lc3）

水平连接有效刚度Khch_deflection41 mn/m

1/（2/Khch_ah+2/Khch_ab+2/Khch_b+1/Khch_c）

2.5 主船体二阶矩

主船体横截面可简化为一箱形截面结构，参数计算流程如下：

桩腿横向间距一半Wh/m 23.774

主船体型深Hh/m 9.45

板有效厚度th/m 0.021

轴向面积/m21.395

扭转刚度Ix=5·Iy/m4125.54

弯曲刚度Iy/m425.11

弯曲刚度（×10）Iz/m41 027.6

2.6 桩腿有效刚度

桩腿有效刚度的计算流程如下：

水深/m 121.92 106.68 99.98

弹性模量E/Pa 2.06E+11 2.06E+112.06E+11

桩腿水平惯性矩I/m415 15 15

下导向至泥面间桩腿

长度L/m 146 133 131

平均最大垂向重量/kn 52 405 52 405 52 405

桩腿屈曲载荷P_E/kn 3.68E+05 4.39E+054.53E+05

垂向刚度因子F_V0.96 0.95 0.95

水平刚度因子F_H0.60 0.58 0.58

弯曲刚度因子F_R0.00 0.00 0.00

极限因子乘积F_R·K_RH9.26E+12 9.26E+129.26E+12

有效刚度K_E/（N·m-1）1.90E+06 2.46E+062.57E+06

2.7 桩腿自然频率

3 有限元方法计算

自升式平台的自由振动有限元计算主船体进行了梁式结构简化，具体方法可参见文献［2］（第5.6.5节），论文中自由振动有限元模型的桩腿结构为详细模型，桩靴和主船体及升桩机构室均做简化处理，有限元模型参见图4～图6。

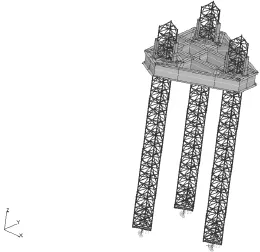
图4 121.92 m水深的有限元模型

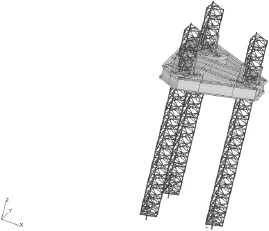
图5 106.68 m水深的有限元模型

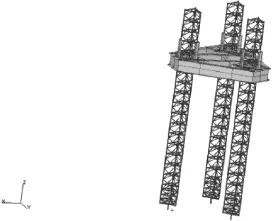
图6 99.98 m水深的有限元模型

有限元模型同样在泥面下3 m作简支处理，三个方向线位移为零，无旋转自由度约束。如图4所示，梁式主船体结构尽量在垂向上体现其质量分布，借助大型有限元软件MSC/PATRAN、MSC/NASTRAN进行直接模态计算，体现桩腿的附连水质量后的自由振动计算结果依次为：10.39 s（99.98 m水深）、10.48 s（106.68 m 水深）、11.67 s（121.92 m 水深）。

4 计算结果分析

由直接简化计算和有限元计算结果，结合该平台基本设计数据，得到如表4所示结果。

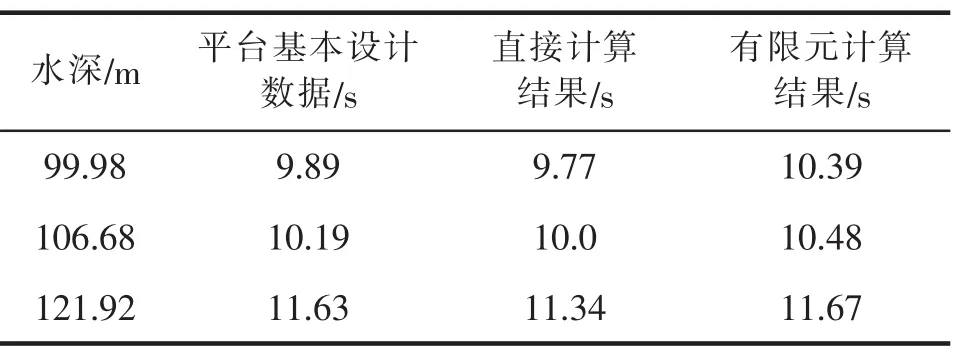
表4 计算结果总结

由此可得出如下分析结论：

（1）初期设计阶段的自由振动计算，两种方法均能达到工程应用的要求；

（2）直接简化计算结果偏低，有限元计算结果偏高；

（3）有限元方法计算时，主船体垂向质量分布对自由振动计算结果影响与水深有关；随着水深的增加，主船体之上的质量分布对自由振动计算结果的影响越来越小；

（4）直接简化计算方法虽过程较为繁琐，但相对有限元计算方法建立在三维有限元的基础上，需对主船体垂向质量分布描述相对准确这一点而言，直接简化计算在前期设计阶段较为方便和有效；

（5）直接简化计算和有限元计算均对泥面下3 m作简支处理，对泥面的支撑属性研究需要在后续工作中进一步展开。

［1］ABS.Guidance notes on dynamic analysis procedure for self-elevationdrillingunits［S］.ABS，Houston：January2004.

［2］SNAME.Guidelines for site specific assessment of mobile jack-up units［S］.Technical&Research Bulletin 5-5 A，January 2002.