On the Nonlinear Matrix Equation X+A*f1(X)A+B*f2(X)B=Q

SANG HAI-FENG,LIU PAN-PAN,ZHANG SHU-GONGAND LI QING-CHUN

(1.School of Mathematics,Jilin University,Changchun,130012) (2.School of Mathematics and Statistics,Beihua University,Jilin City,Jilin,132013)

Communicated by Ma Fu-ming

On the Nonlinear Matrix Equation X+A*f1(X)A+B*f2(X)B=Q

SANG HAI-FENG1,2,LIU PAN-PAN1,2,ZHANG SHU-GONG1,*AND LI QING-CHUN2

(1.School of Mathematics,Jilin University,Changchun,130012) (2.School of Mathematics and Statistics,Beihua University,Jilin City,Jilin,132013)

Communicated by Ma Fu-ming

In this paper,nonlinear matrix equations of the form X+A*f1(X)A+ B*f2(X)B=Q are discussed.Some necessary and sufficient conditions for the existence of solutions for this equation are derived.It is shown that under some conditions this equation has a unique solution,and an iterative method is proposed to obtain this unique solution.Finally,a numerical example is given to identify the efficiency of the results obtained.

nonlinear matrix equation,positive def i nite solution,iterative method

1 Introduction

Denote by P(n)the set of all n×n positive semi-def i nite matrices.In this paper,we consider the class of nonlinear matrix equations

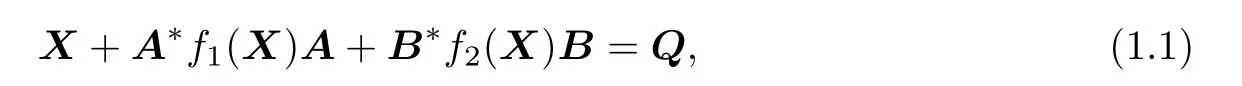
where A is a nonsingular matrix,Q is a Hermitian positive def i nite matrix,f1,f2are continuous maps from P(n)into P(n),and they are either monotone(meaning that 0≤X≤Y implies that f(X)≤f(Y))or anti-monotone(meaning that 0≤X≤Y implies that f(X)≥f(Y)).

Nonlinear matrix equations of the form(1.1)often arise in dynamic programming,control theory,stochastic f i ltering,statistics,and so on.In recent years,these equations have been extensively studied by several authors,and some properties of their solutions have beenobtained.

(1.1)has been investigated in some special cases.Some authors considered(1.1)in the case that f2(X)=0(see[1–2]).Du[3]treated the case that f1(X)=-X-α,f2(X)= -X-βand Q=I,where α,β∈(0,1].For the case f2(X)=0,many authors discussed the equation for particular choices of f1(X)and matrix Q.For example,the case f1(X)=X-1is studied in[4–5],the case f1(X)=X-2and Q=I is discussed in[6],and the case f1(X)=X-nis considered in[7–8].A more general case is f1(X)=X-qwhere q is a positive number,which is discussed in[9–13].Some other authors studied similar equations as in[14–16].

In this paper,we derive some necessary and sufficient conditions for the existence of the solutions of(1.1).And we investigate the uniqueness of the solution,and then we propose an iterative method to obtain this unique solution.Finally,we give a numerical example to identify the efficiency of the results obtained.

The following notations are used throughout this paper.For a positive def i nite matrix A,λmax(A)and λmin(A)stand for the maximal and minimal eigenvalues of A,respectively. A*is the conjugate transpose of the matrix A,and A-*is the inversion of A*.‖A‖denotes the spectral norm of A.A＞0(A≥0)denotes that A is a positive def i nite(semi-def i nite) matrix,and A＞B(A≥B)means A-B＞0(A-B≥0).The notation LA,Bdenotes the line segment joining A and B,i.e.,

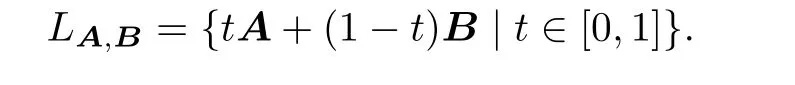
2 On the Positive Def i nite Solutions of(1.1)

Theorem 2.1If fi(D2)=(fi(D))*fi(D),i=1,2,for any nonsingular matrix D,then (1.1)has an Hermite positive def i nite solution if and only if there is a nonsingular matrix W such that

Proof.If X is an Hermite positive def i nite solution of(1.1),then there is a unique Hermite positive def i nite matrix W such that X=W2(see[17–18]).Substituting X=W2into (1.1)gives

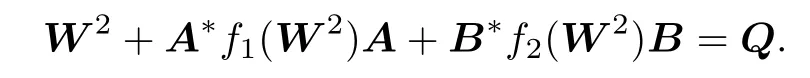
Then we have

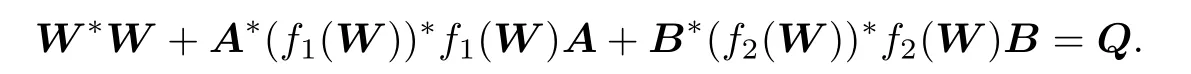
Q is Hermite positive def i nite,so

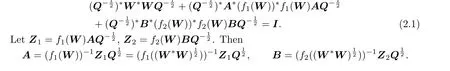
By(2.1)we know that

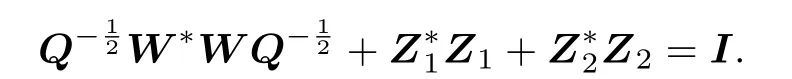
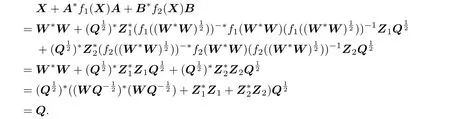
Corollary 2.1Let f1,f2be monotone.If,then(1.1)has a solution in[0,Q].

Proof.If f1,f2are monotone,and,then for all X∈[0,Q], we have

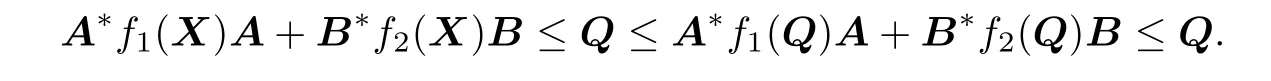
So the condition of Theorem 2.2 is satisf i ed,and then(1.1)has a solution in[0,Q].

Theorem 2.3Let X be a positive def i nite solution of(1.1).If both f1,f2are monotone, and fi(aI)=φfi(a)I,i=1,2,for all a∈R,such that

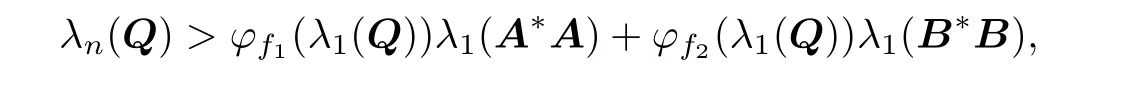
then one has

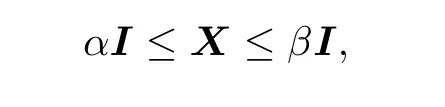
where α and β are the positive solutions of the equations

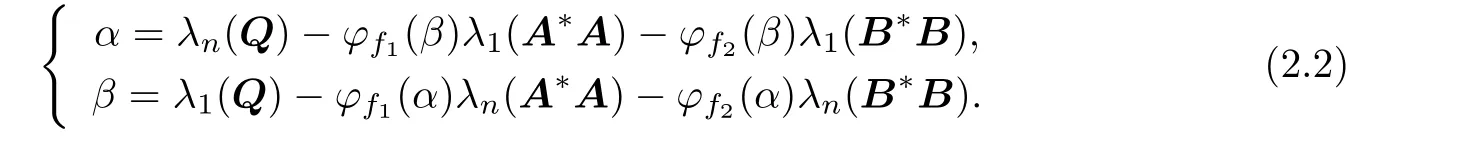
Proof.We def i nite two sequences as follows:

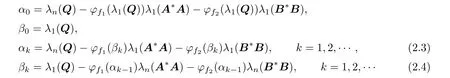
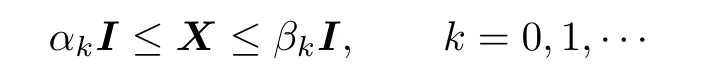
In fact,from the condition of this theorem and the def i nition above we have 0＜α0＜β0. Then

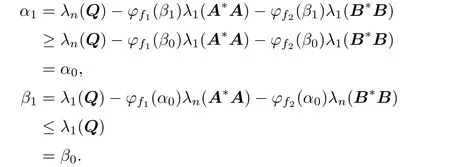
Assume that αk≥αk-1,βk≤βk-1.Then

Therefore,for every k,we have αk+1≥αk,βk+1≤βk.That is,the sequence{αk}is monotonically nondecreasing,and the sequence{βk}is monotonically nonincreasing.

Let X be a positive def i nite solution of(1.1).Then X≤Q≤λ1(Q)I=β0I.f1and f2are monotone,so

and then

Furthermore

that is,X∈[αI,βI].

00

Assume that X∈[αkI,βkI].Then

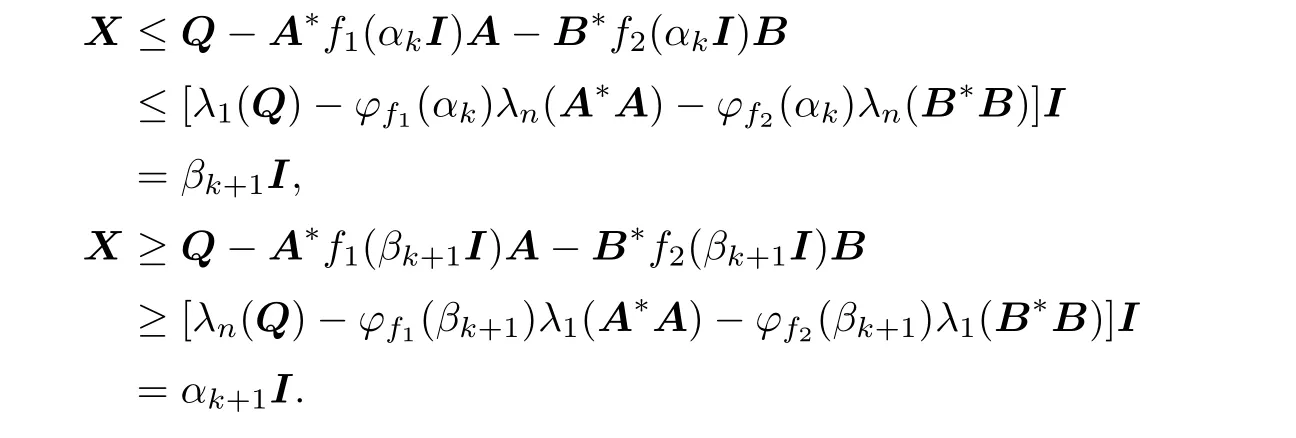
So X∈[αk+1I,βk+1I].By inductive method we can obtain that X∈[αkI,βkI]for every k.Therefore,the sequence both{αk}and{βk}are convergent.

Let

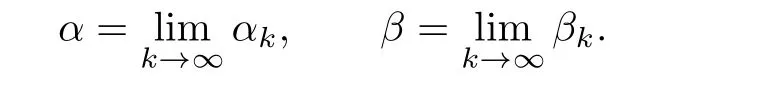
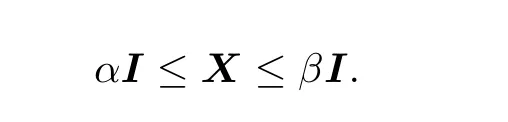
Then By taking the limit on both sides of(2.3)and(2.4)we know that α,β satisfy(2.2)and β≥α≥α0＞0.

Lemma 2.1[4]Let f:U→M(n)(U⊂M(n)open)be dif f erentiable at any point of U. Then

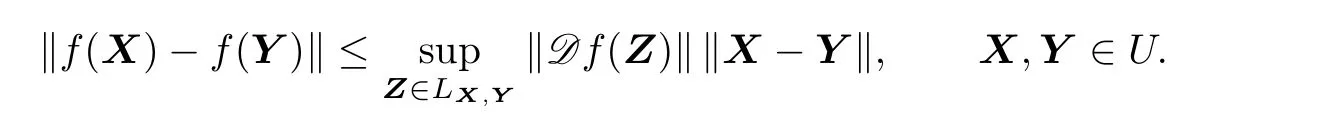
Theorem 2.4Let f1,f2be dif f erentiable at any point of[0,Q],and

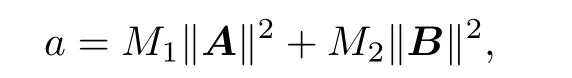
where

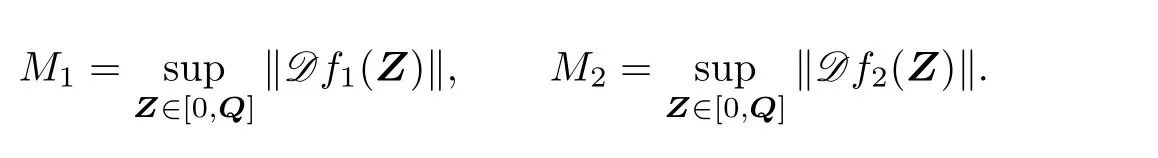
(i)If(1.1)has a solution X on[0,Q],and a＜1,then X is the unique solution on [0,Q];

(ii)Let g:[0,Q]→[0,Q]and g(X)=Q-A*f1(X)A-B*f2(X)B.If a＜1,then(1.1) has a unique solution on[0,Q].Furthermore,we consider the following iterative method:

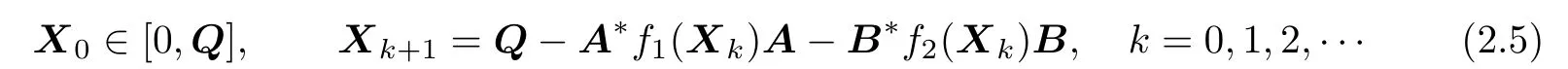
The sequence{Xk}in(2.5)converges to the unique solution X,and moreover,

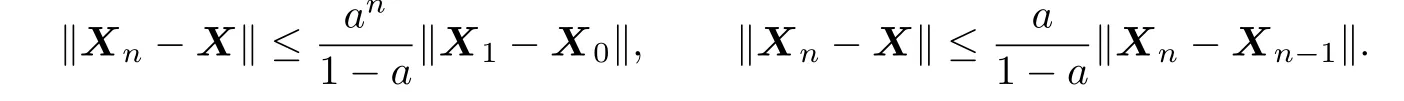
Proof.(i)Assume that X and¯X are two dif f erent solutions on[0,Q].Then from Lemma

2.1 we can obtain

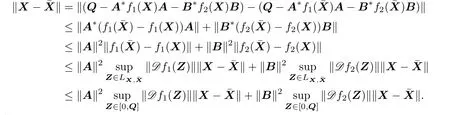
Let

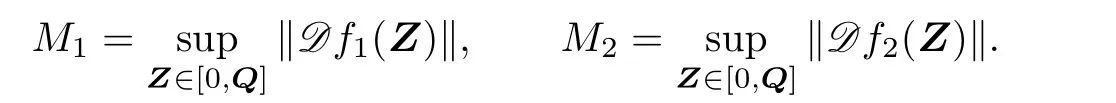
From a＜1 we have

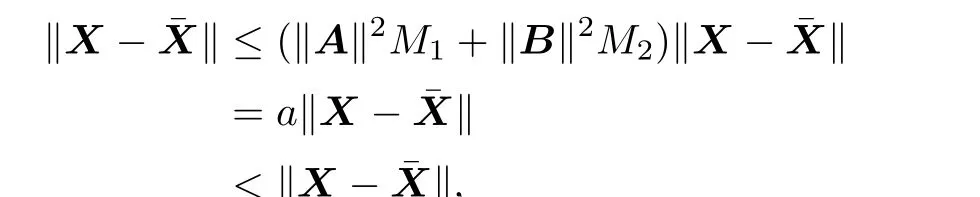
which is a contradiction,so X=¯X.That is,X is the unique solution in[0,Q].

(ii)Let Y1,Y2∈[0,Q].From Lemma 2.1 we have

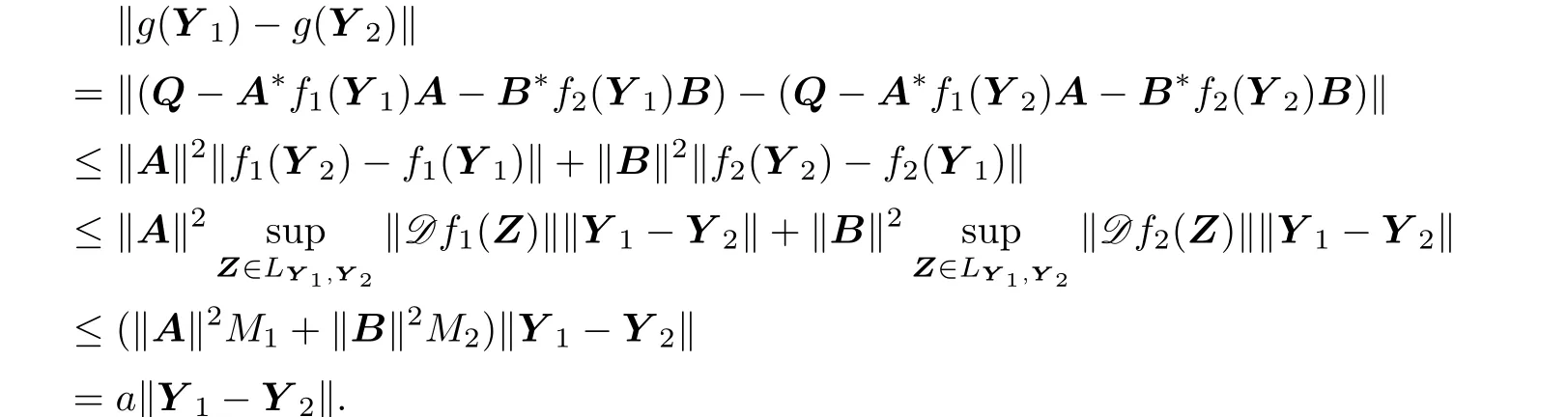
The interval[0,Q]is a complete metric space because it is a closed subset of P(n).And a＜1,so the map g is a contraction on[0,Q].Then it follows from the contractive mapping principle that the map g has a unique f i xed point X in[0,Q].Furthermore,the sequence {Xk}in(2.5)converges to the unique solution of(1.1),and moreover

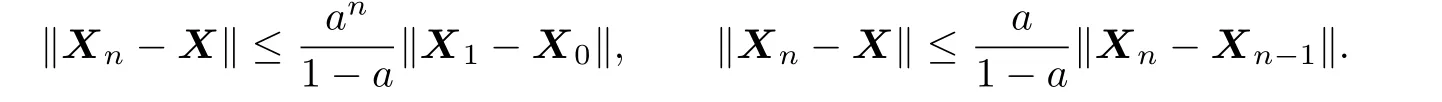
Theorem 2.5Let continuous maps f1,f2be anti-monotone and dif f erentiable at any point of[0,Q].Assume f1(aI)=φf1(a)I,f2(aI)=φf2(a)I,for all a∈R.Consider the following iterative method:

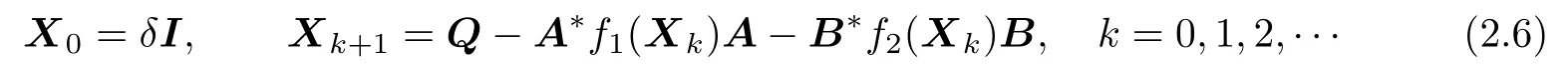
where δI∈[0,Q].If there is a γ∈[0,1]such that

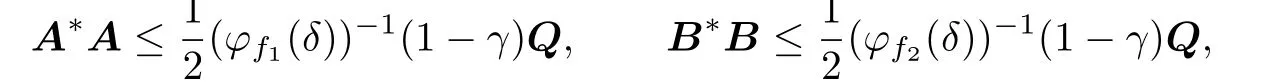
and γλn(Q)≥δ,then the sequence{Xk}in(2.6)converges to a positive def i nite solutionof(1.1).Moreover,

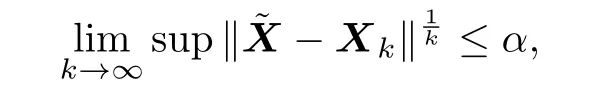
Proof.From the iterative sequence(2.6)we have

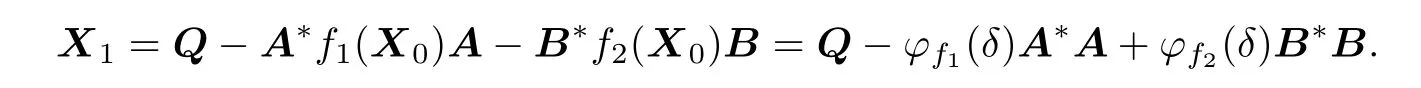
According to the given condition,we have

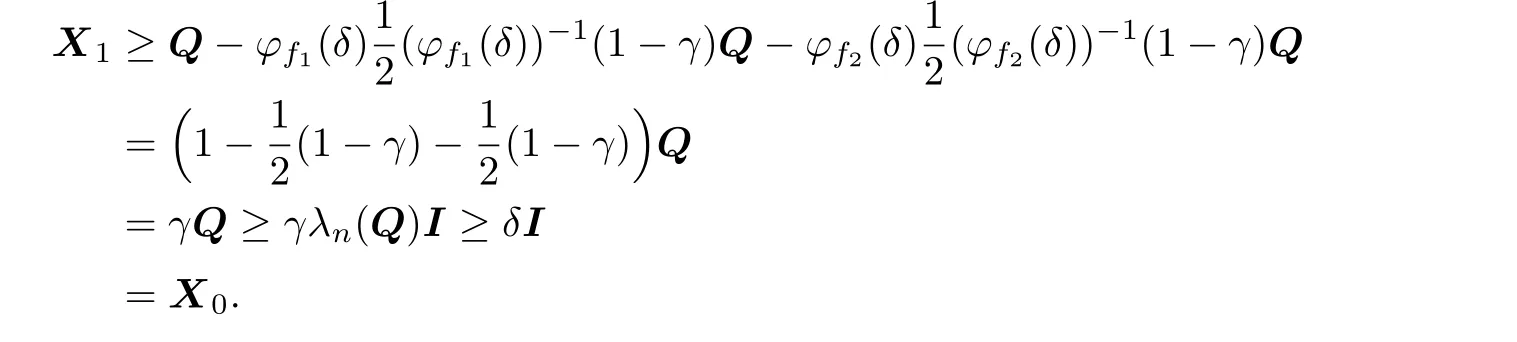
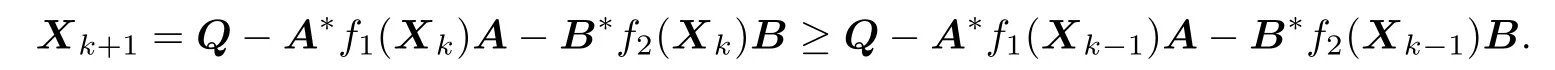
Therefore,the sequence{Xk}is monotonically nondecreasing by inductive method.

Notice that{Xk}is bounded above by Q,so it is convergent,and let its limit be˜X.It is easy to show thatis a positive def i nite solution of(1.1).

From Lemma 2.1 we can obtain

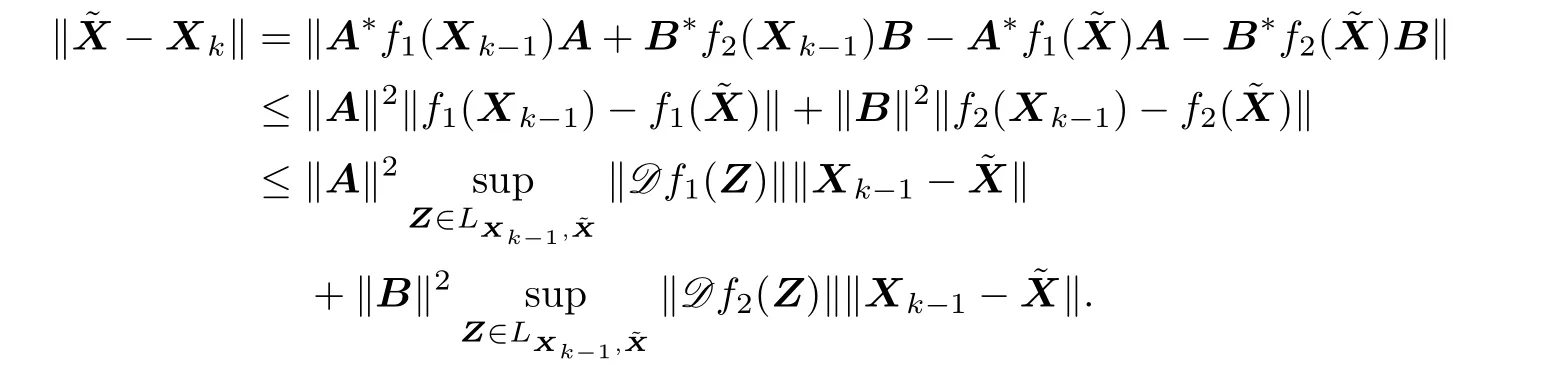
Let

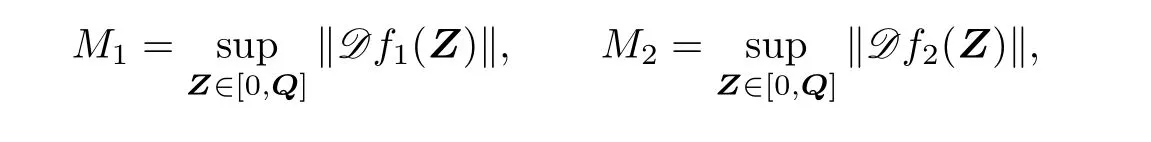
and

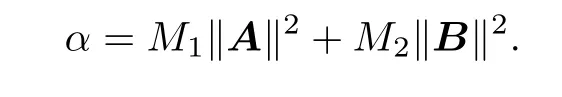
Then

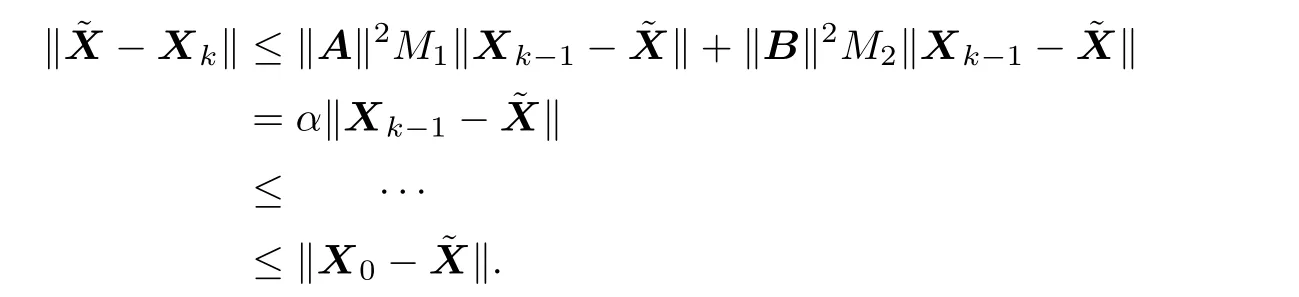
Therefore,

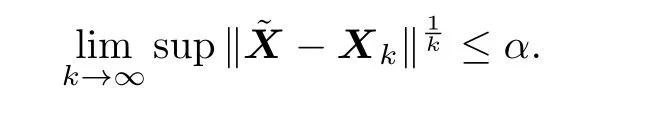
3 Numerical Example

In this section,we give a numerical example by using Matlab to identify the efficiency of the results obtained.

Example 3.1Let f1(X)=X2,f2(X)=X3and Q=I.The equation then becomes

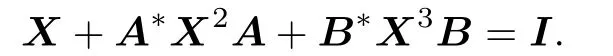
Consider the Frˊechet derivatives of f1and f2:

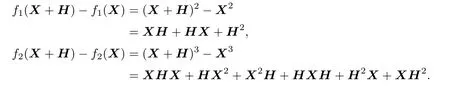
Then we have

So

and

For M1,M2in Theorem 2.4,we have

Thus

Assume that A*A+B*B≤I.Then for X∈[0,I],on the one hand,

on the other hand,

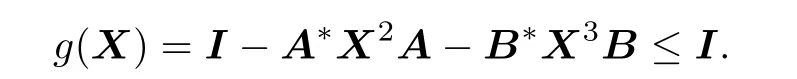
Then g(X)∈[0,I]for X∈[0,I].

From Theorem 2.4,if matrices A and B satisf i es

then the equation has a unique solution in[0,I],and moreover,using the iterative method (2.5)we can obtain this unique solution.

Now we choose matrices A and B as

respectively.It is easy to know that

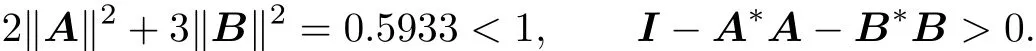
Then the equation has a unique solution in[0,I].

We choose the initial matrix X0=I,and the precision is chosen as 10-9.By the iterative method(2.5),after 19 steps we obtain the following results:

and

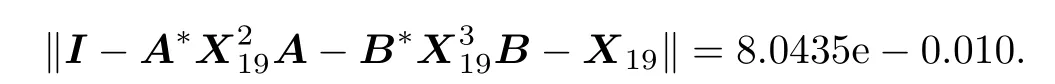
From Theorem 2.4 we know that X19is the unique solution in[0,I].

[1]Ran A C M,Reurings M C B.On the nonlinear matrix equation X+A*F(X)A=Q, solutions and perturbation theory.Linear Algebra Appl.,2002,346(1):15–26.

[2]El-Sayed S M,Ran A C M.On an iteration method for solving a class of nonlinear matrix equtions.SIAM J.Matrix Anal.Appl.,2001,23(3):632–645.

[3]Du Z F.Positive def i nite solution of matrix equation X-A*X-αA-B*X-βB=I.J.Jilin Univ.(Sci.Ed.),2010,48:26–32.

[4]Engwerda J C,Ran A C M,Rijkeboer A L.Necessary and sufficient conditions for the existence of a positive def i nite solution of the matrix equation X+A*X-1A=Q.Linear Algebra Appl., 1993,186:255–275.

[5]Monsalve M,Raydan M.A new inversion-free method for a rational matrix equation.Linear Algebra Appl.,2010,433(1):64–71.

[6]Zhang Y H.On Hermitian positive def i nite solutions of matrix equation X+A*X-2A=I. Linear Algebra Appl.,2003,372:295–304.

[7]El-Sayed S M,Al-Dbiban A.On positive def i nite solutions of the nonlinear matrix equation X+A*X-nA=I.Appl.Math.Comput.,2004,151(2):533–541.

[8]Ivanov I G.On positive def i nite solutions of the family of matrix equations X+A*X-nA=Q. J.Comput.Appl.Math.,2006,193(1):277–301.

[9]Hasanov V I.Positive def i nite solutions of the matrix equations X±A*X-qA=Q(0＜q≤1). Linear Algebra Appl.,2005,404:166–182.

[10]Duan X F,Liao A P.The Hermitian positive def i nite solutions and its perturbation analysis of matrix equation X+A*X-qA=Q(q≥1)(in Chinese).Numer.Math.J.Chinese Univ., 2008,30:280–288.

[11]Wang J F,Zhang Y H,Zhu B R.The Hermitian positive def i nite solutions of matrix equation X+A*X-qA=I(q＞0)(in Chinese).Math.Numer.Sinica,2004,26:61–72.

[12]El-Sayed S M,Petkov M G.Iterative methods for nonlinear matrix equations X+A*X-αA= I(α＞0).Linear Algebra Appl.,2005,403:45–52.

[13]Yin X Y,Liu S Y.Positive def i nite solutions of the matrix equations X±A*X-qA=Q (q≥1).J.Comput.Appl.Math.,2010,59(12):3727–3739.

[14]Yang Y T.The iterative method for solving nonlinear matrix equation Xs+A*X-tA=Q. Appl.Math.Comput.,2007,188(1):46–53.

[15]Liu X G,Gao H.On the positive def i nite solutions of equation Xs±ATX-tA=In.Linear Algebra Appl.,2003,368:83–97.

[16]He Y M,Long J H.On the Hermitian positive def i nite solution of the nonlinear matrix equation. Appl.Math.Comput.,2010,216(12):3480–3485.

[17]Bhatia R.Matrix Analysis.New York:Springer,1997.

[18]Luan T,Guo L.An approach to determine the non-sigularity matrices.J.Beihua Univ.,2013, 14(1):32–34.

A

1674-5647(2013)03-0280-09

Received date:Dec.31,2012.

The NSF(11171133)of China.

*Corresponding author.

E-mail address:sanghaifeng2008@163.com(Sang H F),sgzh@mail.jlu.edu.cn(Zhang S G).

2000 MR subject classif i cation:15A24