80 t 钢包静置过程温降分析
张彩军 王昂 李庆效 朱立光
(1.河北联合大学;2.安徽首矿大昌金属材料有限公司)
0 引言
钢包作为一整个重要的钢水周转设备,对维持中间包内钢水温度稳定有着重要作用[1-2]。合理的温度制度,可以有效的提高铸坯质量、降低运行成本,准确的命中钢水温度已经成为越来越多钢铁公司最为关注的问题之一。
从上世纪60年代开始就有大量的研究人员进行了相关的计算[3-6],其中杜亚伟[7]等人使用Turbo-C 进行了编程对影响钢包的热循环过程进行了研究,对几个温降影响较大的环节提出了改进措施,张李平[8]等人结合首钢225 t 钢包通过建立传热模型对钢水的温降预测进行了仿真计算,准确率达到80%,并计算了不同状态下的钢包补偿温度。从研究方法上来说有钢包热循环过程主要有实测法、物理模拟法、数值模拟法和综合研究方法。其中实测法主要是借助热电偶对钢包实行在线温度研究,而数值模拟就是通过建立一定的传热数学模型,使用了计算机进行模拟计算这其中就包括有简单的数学计算[7]和包含复杂方程的传热模拟[8]。由于这些研究与方法都是需要有较强计算要求,因此在实际生产中并不能在现场中快速的应用,对此应当开发更加简单的方法来进行分析。笔者采用了两种不同的方法:数学解析方法和软件模拟,研究了钢包装入钢水后的散热过程。通过建立一些必要的假设,在保证计算精度的情况下能够较快的得出钢包温度变化曲线,为实际中简单的计算钢包不同状态下温度补偿提供了指导依据。
1 数学解析方法
1.1 非稳态导热的基本概念
在非稳态导热过程中物体内的温度和热流都是在不断的变化,而且是一个不断地从非稳态到稳态的导热过程,也是一个能量从不平衡到平衡的过程。环境对系统(物体)温度分布的影响是很显著的,且在整个的过程中都一直在起作用。对于可以忽略内部温差的非稳态导热过程,采用数学分析法——集总参数法求解温度和过程总传热量。
从该问题出发首先假设钢包为近似的圆柱体,由于包壁厚度对于钢包的直径而言,其值很小,可以近似看作半无限大平板。为此,使用半无限厚物体在第一类边界条件下的一维非稳态导热作为计算公式进行计算,计算中使用的各种材料的热物理参数见表1。

表1 各材料的热物理参数
常物性无内热源一维非稳态导热使用的微分方程为:

对于该定解问题,一般用拉普拉斯变换求解,这里直接给出解的结果为:

在τ 时刻,通过壁面的热通量的确定,由傅里叶定律确定:

则壁面处从τ1~τ2时间内通过单位面积的总热量为:

式中:a——热量传输系数,亦称为导温系数,m2/s;
λ——导热系数,W/(m·℃)。
公式(4)的使用范围为:①不可压缩流体;②导热系数为一个与温度空间无关的数;③流体没有使其体积变化的反应。
1.2 数值计算及结果分析
1)首先计算静置1 min 内的状态。带入公式计算:

代入公式(2)即:
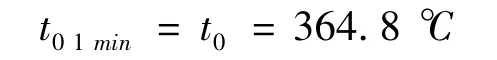
将数据代入(4)可以得出单位面积的总热量为:
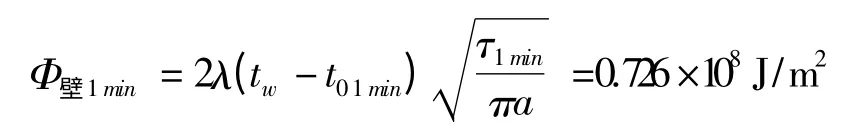
同理计算出钢包底部的单位面积的总热量为:

以钢包中的钢液重量为80 t 为例此时的钢液液面高度约2.5 m,假设钢液时刻都能充分搅拌,即钢液内部没有温差,则钢液每下降一摄氏度放出的热量为:

则这时候的温降为:

式中:S内——钢包内壁面积,m2;
Δt——钢包温降,℃。
代入公式(5),计算得:

对时间在7 min 之内的钢包散热情况都可以重复以上计算步骤,8 min 后钢包壁面的温度波动到达中间面,此时计算需要考虑中间面的温度变化。重复计算至60 min,将每分钟计算的结果绘制成图(如图1 所示)。
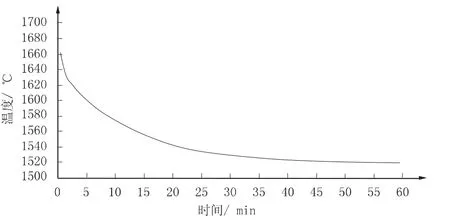
图1 钢包内钢液温度随时间变化的曲线
由图1 中的计算结果可以看出,在钢液静置的前15 min 之内钢液的温降和时间基本呈现线性关系,在40 min 之后钢包平均温度基本保持一致。使用数值计算的方法可以很快的得出钢液温度变化曲线,原理简单可行能够较快速的推广在一线生产中,用于粗略计算钢包温度补偿状况。
2 数值模拟分析
为进一步验证数值计算方法的准确性,同时寻找另一种简单可行的计算方法,考虑到钢液的凝固过程中的密度变化会引起自然流动,使用商业化计算软件fluent 进行传热过程分析,通过建立钢包传热的2D 模型简化计算,各部分耐火保温材料的参数见表1。考虑到钢液的凝固和熔化,相应的参数见表2。

表2 08Al 钢种的物性参数
2.1 网格与边界条件设定
计算中所使用的结构网格如图2 所示,网格数量在10000 左右。

图2 钢包传热计算所使用的模型
1)顶面由于增加钢包盖减少散热,所以认为上顶面为绝热条件;
2)钢包侧面和底面增加有10 mm 的钢板,空气的自由对流换热系数为20 W/(m2·℃),钢包表面温度为60℃;
3)为简化计算不考虑吹氩搅拌等条件的影响。
4)计算中使用的钢包内衬温度为现场中热电偶实际测量温度,以钢包内表层温度710℃设置为工作层温度,以200℃设置为保温层温度。
2.2 数值模拟计算结果分析
使用非稳态计算每60 s 保存一次文件,不同时刻下的钢包内温度场如图3 所示。
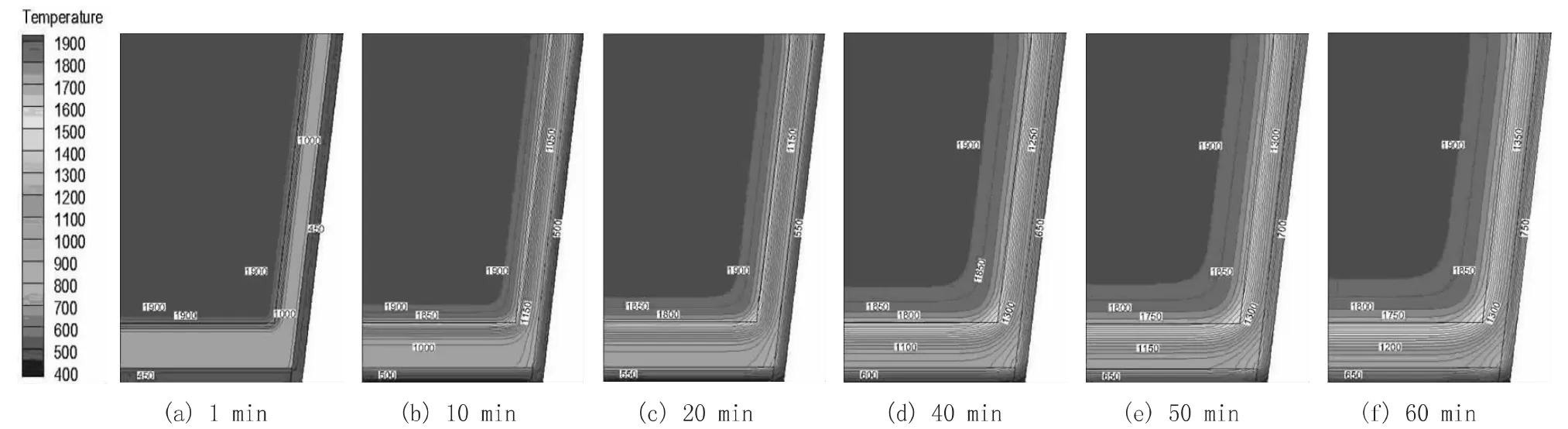
图3 不同时刻下的钢液温度
由图3 可以看出,随着时间的增加钢包内的温度逐渐降低,钢包边缘钢液出现凝固现象。钢液所产生的初期较大的温降主要是用来加热钢包包衬。并且由于钢包底部边缘位置同时向包底与包璧散热所以产生大量的温降。从图中可以很直观的看出在静置40 min 后,钢包包衬耐火材料温度才能基本达到稳定,因此在生产中为了减少钢包的热量散失不仅应当要求钢包烤包温度提高,也要提高烘烤时间,在烤包期间就使钢包包衬温度达到稳定,这样可以极大地减少静置过程中的钢包散热。
不同时刻下的钢包内的钢液状态如图4 所示。

图4 不同时刻下监测点处钢液平均温度曲线
由图4 不同时刻监测点的平均温度变化可以看出,随着时间的推移钢包内的温度不断降低,在前10 min以内温度的降低大致呈直线下降,而后温降逐渐减小,时间在50 min 之后温度就基本稳定。
为减少钢包散热,应当提高钢包工作层与保温层温度,图5 为工作层温度分别为810℃、910℃、1010℃、1110℃时的计算结果。

图5 工作层温度不同时的钢液温度曲线
由图5 中可以看出,保温层温度每增加100℃,静置60 min 后的钢液最终温度增加7℃左右。图6 为保温层温度分别为200℃,300℃,400℃时的计算结果。

图6 保温层不同时的钢液温度曲线
由图6 中可以看出,保温层温度由200℃提高到300℃,钢液温降减小。再继续增加保温层温度对钢液的温降影响变小, 这是由于保温层温度的提高会更快更多的向环境中散失热量,不会影响钢包内部状况。
3 两种计算结果的分析
两种计算方式都同样得出了相同的计算结果,从最终的温度变化曲线上看,在加入钢水的前10 min之内是温降最大的阶段,数值计算方法与软件模拟方法平均每分钟温降分别为6.4℃/min 和7.8℃/min 相差较小,超过50 min 之后温度变化趋势逐渐变缓,最终两者到达的温度分别为1520℃和1508℃。结合实际测量现场数据可以最终发现两者得出的温降数据都与实际相近,前期温度降低速度过快主要就是烤包温度较低,钢液在前30 min 之内是在加热钢包内衬,因此烤包温度较低,且新包烘烤时间不足都会使得钢液的温降增加,为解决这一问题,建议在使用新包时增加烤包时间,而在线烘烤时间也应当适当增加。
通过这两种方法并同时结合现场数据可以看出,这两个模型都能较好的描述钢包静置过程中的温度散失,其中数值计算的方法具有简单易掌握等优点,在保证相当精度的状况下可以推广到实际应用中;而数值模拟的方法则需要采用特定的软件设置,由于考虑到了钢液凝固过程中的自然流动,可以更准确的确定钢包内钢液温度,可以用于更加精确的计算评估中。
4 结论
1)分别使用数值计算与数值模拟的方法对钢包内钢液温度变化进行了预测,两者对钢液温度下降趋势都有较为准确的描述,表明在钢液加入钢包后前10 min 内,温度下降的幅度最大,40 min 之后温度趋于稳定。
2)两种模型都是在保证一定精度前提下,简化了计算难度,适用于在线计算与评估钢包温度,生产应用后初步解决了钢液温度补偿计算困难的问题。
3)增加工作层温度可以有效的减少钢液静置过程的热量散失,工作层初始温度每增加100℃,钢液温度提高7℃左右;保温层温度由200℃提高到300℃,钢液温降减小,再继续提高保温层温度对钢液温降的影响较小,因此应当最大限度提高工作层温度,适当的提高保温层温度。
[1]李晶,张志成.60 t 钢包的传热分析[J].特殊钢,2001,22(2):16-18.
[2]刘占增,郭鸿志.钢包传热研究的发展与现状.钢铁研究,2007,35(1):59-62.
[3]Omotani M A,Heaslip L J.A Mclean.Ladle Temperature Control During Continuous Casting.I&SM,1983(10):29.
[4]沈巧珍,杜建明.冶金传输原理[M].北京:冶金工业出版社,2006:170-180.
[5]张李平,刘斌.225 t 钢包传热数学模型的研究[J].首钢科技,1992 :20-23.
[6]卢翔宇,杨吉春,王宏明.钢包热行为数学模型研究[J].包头钢铁学院学报,2000,19(2):124-127.
[7]杜亚伟,张远强,耿昆,等.170 t 钢包热循环过程瞬态传热计算分析[J].冶金设备,2012(4):31-35.
[8]K.Widdowson.Ladle composition and temperature control[J].Ironmaking and Steelmaking,1981(5):194-200.
[9]刘晓,顾文斌,王洪兵,等.钢包的热分析[J].宝钢技术,1998(5):6-11.

