约束Delaunay四面体剖分在三维地质建模中的应用

余淑娟，郭飞，李想，徐峰

（南京师范大学虚拟地理环境教育部重点实验室，江苏 南京 210046）

0 引言

分析与解决城市规划建设中的环境地质问题，已成为城市发展的当务之急。近年来，随着计算机技术的发展和城市规划建设的需要，利用计算机建立科学、精细、可靠的三维浅层空间地质体模型，指导城市规划建设，逐渐成为计算机和地学领域内研究的重要内容［1］。

三角剖分，尤其是限定的三角剖分一直是近年来计算几何及其相关领域的主要研究课题之一。Delaunay三角网具有优良的几何特性，如空外接圆性质、最小角最大的性质、局部修改性以及良好的边界约束适应能力等，是公认的最优三角网。Delaunay三角化具有很好的理论基础和数学特性，一直在网格剖分中占有重要地位。对于没有限定条件的离散点而言，Delaunay三角剖分的算法已十分成熟，但在引入限定条件后，其剖分算法还是一个研究热点，并不是很成熟。对约束三角网在三维地质建模应用中而言，郝海森等利用含强约束条件的Delaunay不规则三角网构建地层底板的三维空间实体模型［2］；蔡强等采用区域子分和联动剖分算法实现了地质结构重叠域的限定Delaunay三角剖分［3］；陈永锋等对传统凸包生成、三角剖分和空外接圆检测等算法进行了改进，对地质面进行Delaunay三角剖分［4］；孟永东等依据带约束Delaunay三角剖分算法分别生成地层、断裂、界线类地质结构的TIN模型，拼合形成工程整体三维地质模型［5］。综合考察现有的研究成果［2－10］，大多数集中于通过Delaunay三角剖分构建地质结构TIN模型，对于利用地质层面Delaunay三角网为约束条件直接构建四面体地质体模型方面，目前还需要进一步研究。

本文考虑到Delaunay三角剖分良好的边界约束适应能力，基于钻孔数据插值处理，提出了一种以地质层面Delaunay三角网为约束条件的四面体剖分地质建模方法。首先，将研究区域边界离散，根据研究区域内钻孔勘察资料的空间分布，自适应的在数据相对稀疏的地区添加用于插值处理的虚拟钻孔，采用克里金插值算法计算出虚拟钻孔中和边界点的地层底板埋深数据；其次，对原始钻孔和虚拟钻孔数据以及限定的研究区域边界构建每个地层面的Delaunay三角网；再次，以地层面三角网和钻孔数据及其空间分布信息为约束，构造地质几何模型；然后，以该几何模型作为输入的分段连续线性组合物（Piecewise Linear Complexes，PLC）［11］限定条件，设置四面体的体积或者半径边长比进行网格质量控制，构建三维地质四面体实体模型，并借助VTK（Visualization Toolkit）组件库实现了该地质模型的可视化。

1 三维地质模型

三维地质建模（3DGeological Modeling）也可称为三维地学建模、三维地质数字化建模等，指在获取原始地质勘测数据（如地质点、钻孔、平硐、航拍片等）的基础上，通过对地质实体对象拓扑信息的解译和几何形态的确定，将各种信息综合形成一个复杂整体三维模型的过程。三维地质建模技术就是为了解决地学领域中遇到的三维问题而提出的，如三维地层、断裂、矿体和巷道的显示以及三维巷道的空间拓扑分析、三维矿体的体积与储量计算等问题。

三维地质建模常用方法包括块段构模法、线框构模法、表面构模法及实体构模法［12］。有很多方法可以用来表达表面，如等高线模型、网格模型等，最常用的是TIN模型。实体构模法包括四面体法、六面体法及三棱柱法等，目前利用三棱柱体元构建地质体模型的研究比较成熟［13－15］。本文针对城市地下浅层空间，以地质层面Delaunay三角网及钻孔点为约束条件进行四面体剖分实现层状地质实体的三维地质体模型方法属于实体构模法，该方法能够得到可视化效果较好的地质模型，并可高效地支撑地学空间分析与计算，为城市规划提供更好的决策支持。

2 算法描述

2.1 钻孔数据预处理与插值处理

本文以地质层面Delaunay三角网为约束条件进行四面体地质建模的方法，对钻孔数据的格式有一定的要求，必须对原始钻孔数据进行处理。原始的钻孔数据点在纵向是深度递增值，根据孔口坐标与地层分界点的水平偏移量（或是方位角），计算钻孔数据点（地层分界点或切穿点）的水平坐标，同时给这些点赋予地层属性，为后续三维构模提供方便。

由于建模研究区域内钻孔资料分布极不均衡，直接利用原始的钻孔资料难以构建相对精确、完整且具有良好可视化效果的三维地质体模型。因此，需要对原始分布不均匀的钻孔数据进行适当的空间插值处理以获取地层层面信息。本文根据用户指定的添加插值点的间距，离散研究区域边界，添加边界插值点；规则离散研究区域内部，添加内部插值点；根据原始钻孔勘察资料分布情况，将靠近（距离小于用户指定的间距值）原始钻孔点的插值点移除；最后在边界插值点和内部插值点处进行插值处理，采用克里金插值算法，利用原始钻孔勘察资料计算新增插值点的地层参数。

2.2 约束Delaunay三角／四面体剖分算法

Delaunay三角网具有优良的几何特性，是公认的最优三角网。Delaunay三角剖分有两条重要的性质：圆形准则和最大－最小角准则，后者保证了Delaunay三角剖分是当前点集的最优剖分。

在实际应用中，往往要求生成的Delaunay三角网满足一些约束（限定）条件：在二维情况下有约束点、约束线，在三维情况下还包括约束面。在上述约束条件下生成Delaunay三角网格的过程称作约束Delaunay三角剖分，也称为限定Delaunay三角剖分。在本文地质建模中，地质结构中的二维约束条件的输入格式为平面直线图（Plane Straight Line Graph，PSLG），此格式为点与线段的集合［11］，如图1的PSLG范例所示。

图1 PSLG范例Fig.1 PSLG example

三维约束条件的输入格式为分段连续线性组合物（PLC），此格式是节点、线段与刻面的集合［11］。节点和线段的定义与PSLG相同，刻面可以是复杂或不规则的多边形，也可能有数条边、可能不是凸面状，刻面上可能有洞、裂缝或节点，但刻面永远是平面。三维空间中任何由平面片、直线段和点构成的限定条件经过有限次的运算后都可以转换成规范的PLC限定条件，如图2PLC范例所示。

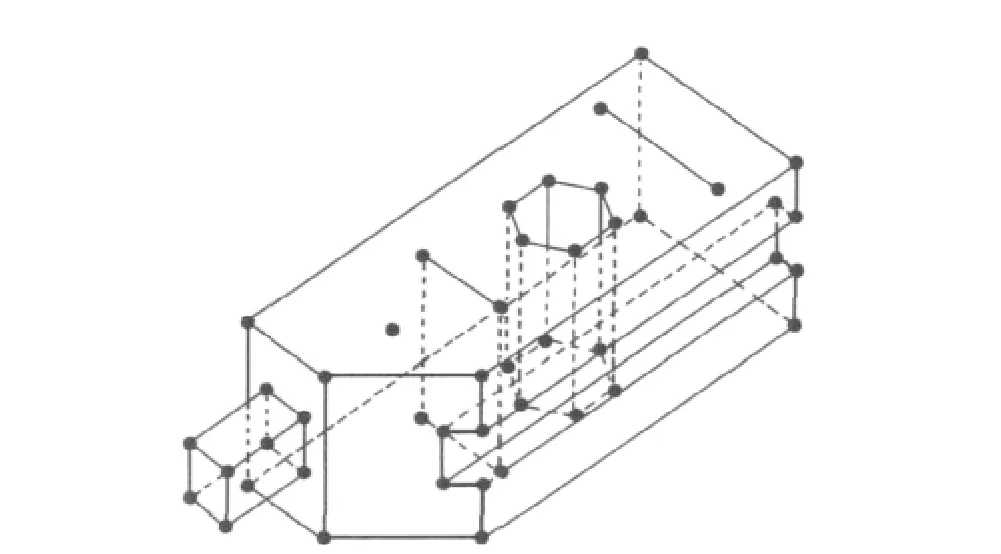
图2 PLC范例Fig.2 PLC example

约束Delaunay三角剖分（CDT），允许在域中加入额外的点从而使得域的所有边界存在于剖分结果中，剖分后的所有单元均不包含其他可视节点，但并不是所有单元均符合Delaunay准则。由于对边界的细化处理加入了新的节点，导致初始剖分点集是最后的剖分点集的子集。

CDT的可视性：如图3a、图3b所示，粗线为输入的线段，三角形t与边e外接圆内都有两个侵入的节点，这两节点对t或e而言都是“不可视的”，因为都被输入线段挡住。三维CDT则增加了刻面对输入节点的可视限制。如图3c所示，粗线为三维的CDT四面体，而此四面体的外接球内有一个节点存在，但被其阴影的刻面遮蔽了，则是不可视的。

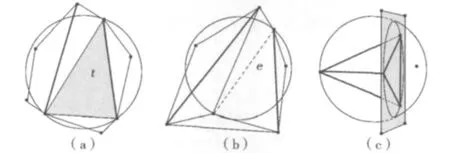
图3 节点可视性Fig.3 The visibility of vertex

约束Delaunay三角／四面体剖分新增点原则：1）侵入线段：当输入线段的径圆／径球包含其他节点即被其他节点侵入时，则新增此线段的中点。2）侵入刻面：当输入刻面的赤道球被其他节点侵入时，则新增此赤道球的球心即刻面的外接圆圆心。但若新增的圆心侵入了某条线段的径球时，则删除此圆心，改为新添此线段的中点。

约束Delaunay三角／四面体剖分方法如下：1）边界离散。将输入的PSLG或PLC中的线段和刻面离散成小的线段或者小三角形。2）点集Delaunay三角／四面体剖分。将离散后的所有顶点集合及约束点集合采用Bowyer－Watson算法［16］进行点集的Delaunay三角／四面体剖分。3）边界恢复。对每个小线段和三角形检查其在三角／四面体网格中的存在性，如果一个小线段和小三角形在网格中不存在，则利用CDT的可视性对其进行恢复。4）新增节点。若边界线段和三角形被其他节点侵入则按照对应的新增点原则对其进行细分以减小线段和三角形的尺度，直到所有小三角形和小线段都不被其他节点侵入。5）网格质量控制。若网格单元超出给定的网格质量限制参数（三角形的最小角或最大面积／四面体的半径边长比或体积），则插入其外接圆／外接球的圆／球心，并遵守Delaunay外接圆／球定理［17］。但是若新添的圆／球心侵入了某小线段或者小三角形，则删除此圆／球心，按照步骤4添加点。6）删除边界以外的网格单元，算法结束。

2.3 构建地质体模型算法

三维地质建模方法主要有模块法、线框法、实体法、表面法4种，本文针对地下浅层空间提出的以地质层面Delaunay三角网为约束条件进行约束四面体剖分构建地质体模型的算法属于实体法。该算法在对原始钻孔数据进行预处理和插值处理后，提取区域边界线，删除边界外的钻孔点（包括虚拟钻孔点），利用剩余的钻孔点以及边界构建各层面约束条件PSLG，依照前述三角剖分算法进行层面Delaunay三角剖分。在层面三角网的基础上，结合钻孔数据及其空间分布信息构建地质体约束条件PLC，根据设定的体积或者半径边长比控制网格质量，对PLC进行约束Delaunay四面体剖分，最后利用VTK组件库对建模结果进行可视化。

3 实例分析

采用本文的地质体建模方法，以南京市河西地区为研究区域，构建了该区域的四面体三维地质模型。图4a为对钻孔数据进行插值处理且删除区域外钻孔点后的钻孔点及区域边界线即为各地质层面的约束Delaunay三角剖分的限定条件PSLG。图4b为地质体四面体剖分约束条件PLC，共有5层约束三角网。根据上述PLC及用户指定的网格质量控制参数，运用前述算法进行地质体约束Delaunay四面体剖分，构建地质体模型，其可视化结果如图4c和图4d所示。可以看出，本文的算法能够成功地对层状地质体进行约束Delaunay四面体剖分，并且可以设置四面体的体积或者半径变长比进行网格质量控制，改善网格单元的质量，构建良好的三维地质体模型。

图4 构建地质体模型实例Fig.4 The example of constructing geological model

算法实现环境为微机环境，CPU为Pentium IV 2.0GHz，内存为2GB，软件环境为 Windows XP Professional版，算法使用C＃语言实现，结合VTK组件库进行可视化，在Visual Studio 2008编译环境下编译通过。

4 结论

本文考虑到Delaunay三角剖分良好的边界约束适应能力，提出了以地质层面Delaunay三角网为约束条件进行四面体剖分的地质建模算法。该算法针对地质钻孔数据稀疏且分布不均匀的问题，采用空间插值算法进行了适当的内插，利用边界约束和钻孔点约束构建了各地质层面的约束Delaunay三角网，在此基础上，结合钻孔数据及其空间分布信息构建地质体约束，根据设定的最大体积或者半径边长比控制网格质量，进行四面体剖分构建三维地质实体模型，借助VTK组件库进行模型可视化。实例证明本文提出的算法是可行的，可得到可视化效果良好的四面体地质模型，且可高效地支撑地学空间分析与计算，为城市规划提供更好的决策支持。

［1］ 金江军，潘懋，曲红刚，等.三维地质建模及其在地下空间开发中的应用［J］.信息技术，2007（3）：26－29.

［2］ 郝海森，吴立新.基于强约束Delaunay－TIN的三维地学模拟与可视化［J］.地理与地理信息科学，2003，19（2）：15－18.

［3］ 蔡强，杨钦，陈其明.地质结构重叠域的限定Delaunay三角剖分研究［J］.计算机辅助设计与图形学学报，2004，16（6）：766－771.

［4］ 陈永锋，陈晓鹏，魏丽英.基于钻孔数据的地质面Delaunay三角剖分［J］.金属矿山，2009（9）：120－122.

［5］ 孟永东，徐卫亚，田斌，等.基于带约束三角剖分的三维地质建模方法及应用［J］.系统仿真学报，2009，21（19）：5985－5989.

［6］ 李培军.层状地质体的三维模拟与可视化［J］.地学前缘，2000（7）：271－277.

［7］ 孟宪海，杨钦，李吉刚.基于层面结构的三维闭合地质区块构造算法［J］.北京航空航天大学学报，2005，31（2）：182－186.

［8］ 红雄，张建勋.基于TIN和STP的3D地学混合构模［J］.工程图学学报，2006（4）：47－71.

［9］ 刘少华，吴东胜，罗小龙，等.复杂地质体的三维建模与可视化方法的研究［J］.矿业研究与开发，2007，27（2）：56－58.

［10］ 蔡强，李海生，左敏，等.基于Delaunay三角剖分的复杂地质结构建模［J］.金属矿山，2010（4）：126－130.

［11］ PREPARATA F P，SHAMOS M I.Computational Geometry［M］.New York／Berlin：Springer－Verlag，1985.

［12］ HOULDING S W.3DGeoscience Modelling：Computer Techniques for Geological Characterization［M］.London：Spring－Vetlag，1994.

［13］ 张煜，白世伟.一种基于三棱柱体体元的三维地层建模方法与应用［J］.中国图象图形学报，2001，6（3）：285－290.

［14］ 齐安文，吴立新.基于类三棱柱的三维地质模拟与拓扑研究［J］.矿山测量，2003（3）：65－67.

［15］ 车德福，陈学习，吴立新，等.基于广义三棱柱体元的三维地层建模方法［J］.辽宁工程技术大学学报，2006，25（1）：36－38.

［16］ EDELSBRUNNER H.Geometry and Topology of Mesh Generation［M］.England：Cambridge Univ.Press，2001.

［17］ SI H，GÄRTNER K.Meshing Piecewise Linear Complexes by Constrained Delaunay Tetrahedralizations［A］.Proceedings of the 14th International Meshing Roundtable［C］.California／San Diego，2005.147－163.