Parameters Estimation of Chaotic Telemetry System between Two Different Time-delayed Chaotic Systems

WEI Heng-dong

(Southwest China Institute of Electronic Technology,Chengdu 610036,China)

1 Introduction

Chaotic telemetry is a new technology in aircraft telemetry system.It completes telemetry system parameters transmission andmeasurement through utilizing chaotic sequence substitute traditionalpseudo code sequence[1-2].The basic principle of chaotic telemetry is that the transmitter uses high-speed chaotic sequence to modulate the transmitted message to spread its spectrum,then,the receiver uses synchronization circuit to generate same chaotic sequence to correlate with the received signal to recover telemetry data and estimate the telemetry parameters.The usually used chaotic telemetry modes are chaotic spread spectrum[3]and chaotic modulation[4].As a non-cooperator,how to get useful information from intercepted chaotic telemetry signal is an important task.However,the report about non-cooperate chaotic telemetry signal analysis is too few.

One interesting application of chaos synchronization is estimation of the system parameters with the available time series from the driving system.During the past decade,an approach of using synchronization as a param-eter estimation method called auto-synchronization[5-6]has attracted much attentions[7-13].This process is governed by additional update rules for the parameters that are controlled by the synchronization error.

The parameter estimation of chaotic telemetry system and getting useful information hidden in intercepted signal by chaotic synchronization is an important issue in chaotic telemetry signal analysis.However,the precondition of most of the parameters estimation methods is that the two systemswhich synchronize with each other should have the same structure,which,however,is not the case in practice.For instance,in chaotic telemetry signal reconnaissance,the non-cooperative detector doesn′t know the system structure.That is to say,the detector has to use a different system to estimate the parameters modulated by information.However,the synchronization and parameter estimation of different chaotic systems is far less understood because of their different structures and parameters.So,it is not only of theoretical interest but also of practical value to investigate the parameter estimation between two different chaotic systems.The immediate configuration for synchronization between two different systems is generalized synchronization.The basic idea of generalized synchronization is that there exists a transformation which is able to map asymptotically the trajectories of the driving attractor into the response attractor.So,if the generalized synchronization is used to parameter estimation,the first problem we must face is the estimation of the “transformation”.However,this transformation is so complex that we can not get any analytical results[14-15].Therefore,designing a simple scheme to estimate parameters between two different chaotic systems is a significant issue.

In thispaper,synchronization based parametersestimation between two different chaotic systems is proposed and applied to chaotic telemetry signal analysis.A control signal is designed based on Krasovskii-Lyapunov theory to make these two systems synchronize with each other.An analytical approach to the sufficient condition for synchronization and parameter estimation is also established.Chaotic telemetry is an active branch of TT&C communication,because of the noise-like characteristic of chaotic signal.Here,as an eavesdropper,a different system is used to decode the message transferred between the cooperators.Firstly,a control signal is designed for parameter estimation between two different chaotic systems based on Krasovskii-Lyapunov theory.The sufficient condition for synchronization and parameter estimation is established analytically.Secondly,the method is verified by numerical examples.Then chaotic telemetry signal reconnaissance scheme is given,too.Finally,results are summarized.

2 Parameters Estimation Scheme

Consider the following time-delay system,

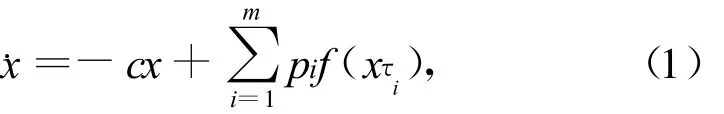
where p=(p1,p2,…,pm)∈Rmare unknown parameters to be estimated;xτ=x(t-τ).This system is used to drive a response system,

where a,b are positive parameters;τ is the delay time.The response system,called prototype model,is proposed as a chaos generator and is studied in Reference[16].Figure 1(a)shows the chaotic attractor of this system,where a=1.7,b=1 and τ=1.Our aim is to design a control signal u and parameter update rules gi(i=1,2,…,m)such that the system(2)synchronize with system(1)and the unknown parameters are estimated correctly.

Fig.1 Phase portrait of the prototype model and Ikeda system图1 Prototype模型和Ikeda系统的相图

Introduce a control signal u to system(2),which can be written as

To determine the control signal and parameter update rules,we investigate the dynamics of the differences Δ=x-y.Then the dynamics of the error are

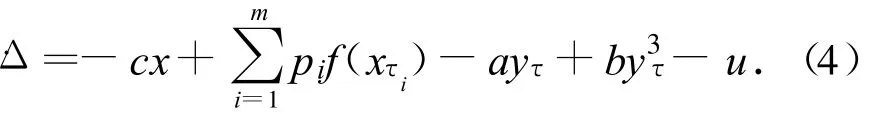
Let ei=pi-qiandcy+kΔ,then

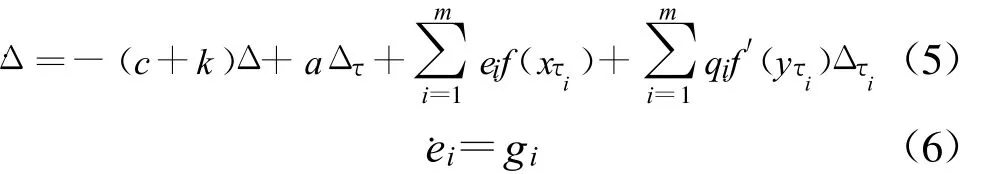
where giare the update rules to be determined to ensure the parameter estimation;qiare the estimation of pi;k is the coupled strength.

According to Krasovskii-Lyapunov theory,we define a continuous positive-definite Lyapunov function[14,17]

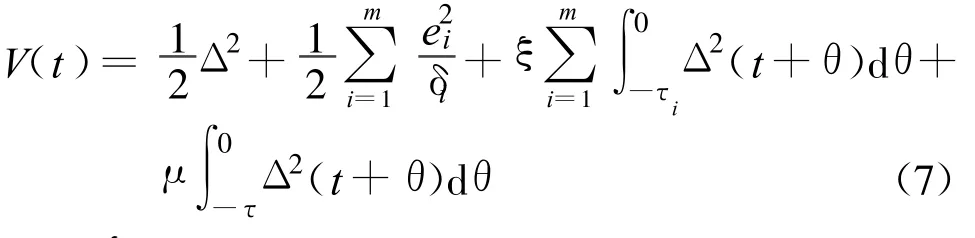
where ξ>0, μ>0 and δi>0 for all i is the update rate.Then

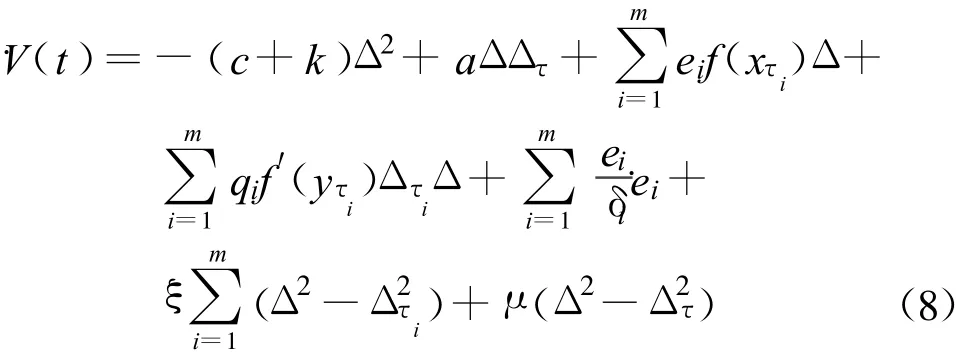
In view of Krasovskii-Lyapunov theory,﹒V will be negative if and only ifand

On the other hand,

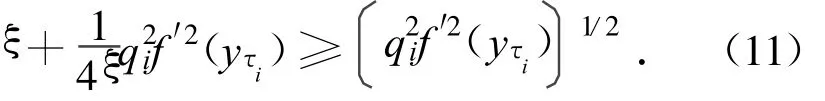
Then,we get the sufficient condition for synchronization and parameter estimation as

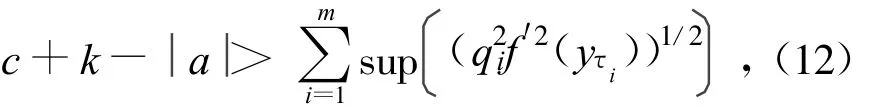
where sup(f(x))is the supremum of f(x).

3 Numerical Simulation

To illustrate the suggested parameter estimation method,we first consider the Ikeda system with one unknown parameter,

where f(x)=sin(x).We choose the parameter values as c=1,p=4 and τ1=2.Figure 1(b)shows the chaotic attractor of this system.Here p=4 is the only estimated parameter.

Another chaotic system,referred in last section,whose structure is different from Ikeda system,

where a=1.7,b=1,τ=1,is used to estimate the unknown parameter.We design the control signal u=qf(yτ1)+.The parameter update rule is

If we choose δ=10,from the condition(12),one can obtain the sufficient condition for synchronization and parameter estimation as k>1.2.Figure 2 shows the synchronization error and parameter estimation of these two different systemswhen k=2.5.Although,these two systems have different structure,it is easy to see from the figure that the synchronization error diminishes gradually.At last,the parameter is estimated correctly as shown in Fig.2(a).Noting that,the update rate δcontrols the convergence speed of the parameter estimation.Improper chosen of update rate will lead to the too slow converge,serious fluctuate,or divergence.

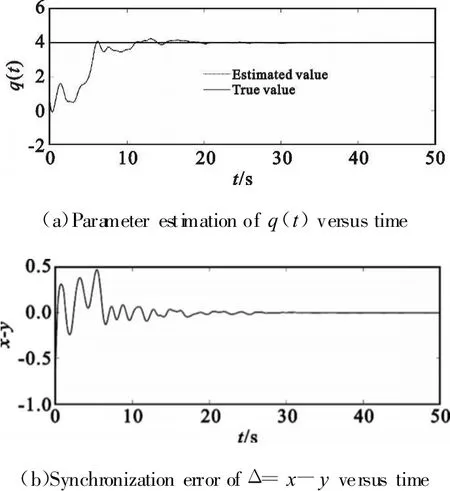
Fig.2 Parameter estimation and synchronization error between Ikeda system(with one unknown parameter)and prototype model图2 Ikeda系统(具有一个未知参数)和Prototype模型之间的参数估计和同步误差

4 Applications

Owing to the random noise-like properties and the discovery of the synchronization of chaotic system,chaotic signals are applicable to secure communication systems[18],including chaotic encryption and chaotic spread spectrum systems.Chaotic telemetry is a new technology in aircraft telemetry system which is an active branch in chaotic communication.In chaotic telemetry scheme with coherent receiver,the transmitter and the receiver use the same chaotic system to encoding and decoding the message,respectively.Here,as an eavesdropper,we use a different chaotic system to decode the useful information transmitted by the transmitter.The Ikeda system,as described in(13),is used to transmit information between the cooperators.The receiver uses the same system to recover the message as

The modulation parameter p is switched between 4 and 5 in the transmitter according to the digital message.That is to say,when the transmitted message bit is 0,the parameter p is set to be 4;when the transmitted message bit is 1,the parameter p is set to be 5.Figure 3 shows decoding by the cooperator and the eavesdropper.The eavesdropper use a different system as

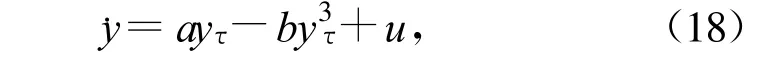
to obtain the useful message,where the control signal u=qf(yτ1)+-axτ-cy+kΔ and the parameter update rule is the same as(17).We choose the parameter values as a=1.7,b=1,τ=1,τ1=2,δ=30 and k=8.Figure 3(a)shows the data m(t)needs to be transmitted.The recovered data m′(t)by the cooperator and the eavesdropper are shown in Fig.3(b),respectively.For better visualization,the parameter q has been divided by 5,and then the estimation by eavesdropper has been added by 2.The solid line denotes the data recovered by the cooperator,and the dashed line denotes by the eavesdropper.Synchronization error versus time is shown in Fig.3(c).For better visualization,we add the synchronization error of the eavesdropper system by 0.5 which are denoted by dashed line.The synchronization error of the cooperator system is denoted by solid line.It is easy to see,the same as the identical system,the different system can be used to estimate the unknown parameter correctly.The synchronization error changesobviously when the parameter switches.Thismainly results from the trajectories switches between the different synchronization manifolds.Noting that,the synchronization error can be used to pre-estimate the code rate to some extent.

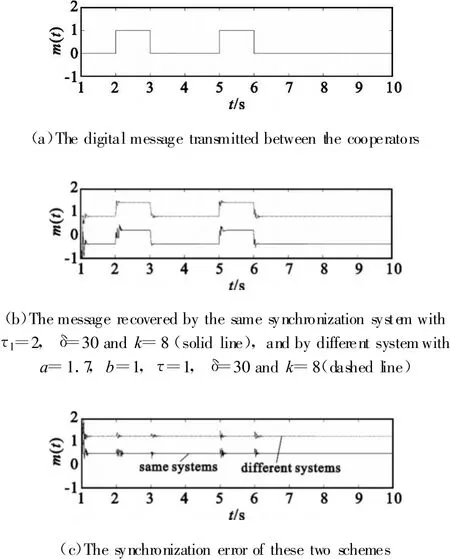
Fig.3 Parameter estimation of chaotic telemetry system using same and different system图3 相同和不同混沌系统对混沌遥测系统参数估计结果

It should be noted that our scheme can be extended to parameter estimation of multi-parameter chaotic telemetry system.Every transmitted telemetry parameter exploits a chaotic system parameter to modulate it.

5 Conclusions

Parameter estimation between two different time-delayed chaotic systems and its application has been investigated.A control signal is designed to ensure synchronization and parameter estimation of different systems based on Krasovskii-Lyapunov theory.This scheme can be used to estimate multi-parameters of a chaotic telemetry system from a scalar observable signal.We exploited a different system to recover the message transmitted between the cooperators.The update rate which determines the convergence speed will decrease the fluctuant time till the correct parameter value is estimated,with the increase of it.So,in chaotic telemetry signal reconnaissance,we can increase the update rate to decrease the convergence time to satisfy the fast parameter switch.An immediate result of the increase of update rate is the serious fluctuation of the initial stepsof parameter estimation.However,a filter can be used to smooth the estimated curve,and a decision device is used to decide the message transmitted from the transmitter.Therefore,our results can be used to practical engineering application.

It is worth noting that the construction of the parameter estimation scheme does not consider the effect of the noise,however,this is an important problem should be faced and solved in synchronization based parameter estimation between chaotic systems.Next,we will study the impact of the noise on our scheme.

[1] WEI Heng-dong.A study on the detection of chaotic direct sequence spread spectrum signal an chaos synchronization[D].Chengdu:University of Electronic Science and Technology of China,2010.(in Chinese)魏恒东.混沌直扩信号检测与混沌同步研究[D].成都:电子科技大学,2010.

[2] LIU Jia-xin.Spacecraft TT&C and Information Transmission Technology[M].Beijing:National Defense Industry Press,2011.(in Chinese)刘嘉兴.飞行器测控与信息传输技术[M].北京:国防工业出版社,2011.

[3] Parlitz U,Ergezinger S.Robust communication based on chaotic spreading sequences[J].Physics Letters A,1994,188(2):146-150.

[4] Stavroulakis P.Chaos applications in telecommunications[M].New York:CRC Press,2006.

[5] Parlitz U.Estimating model parameters from time series by autosynchronization[J].Physical Review Letters,1996,76:1232-1235.

[6] Parlitz U,Junge L,Kocarev L.Synchronization-based parameter estimation from time series[J].Physical Review E,1996,54(6):6253-6259.

[7] Wei H,Li L.Estimating parameters by anticipating chaotic synchronization[J].Chaos,2010,20(2):023112.

[8] Li Z,Zhao X.Generalized function projective synchronization of two different hyperchaotic systemswith unknown parameters[J].Nonlinear Analysis:Real World Applications,2011,12(5):2607-2615.

[9] Zhou P,Ding R.Modified Function Projective Synchronization between Different Dimension Fractional-Order Chaotic Systems[J].Abstract and Applied Analysis,2012(2012):1-12.

[10] Wu X,Li S.Dynamics analysis and hybrid function projective synchronization of a new chaotic system[J].Nonlinear Dynamics,2012,69(4):1979-1994.

[11] Parlitz U,YU D.Synchronization and control based parameter identification in Intelligent Computing based on Chaos[M].Berlin:Springer,2009:227-249.

[12] Wang S,Yu Y.Generalized Projective Synchronization of Fractional Order Chaotic Systems with Different Dimensions[J].Chinese Physics Letters,2012,29(2):020505.

[13] Wei W,Li D H,Wang J.Synchronization of hyperchaotic Chen systems:a class of the adaptive control[J].Chinese Physics B,2010,19(4):1-11.

[14] Ghosh D,Banerjee S.Adaptive scheme for synchronizationbased multiparameter estimation from a single chaotic time series and its applications[J].Physical Review E,2008,78(5):056211.

[15] Pecora L,Carroll T,Johnson G,et al.Fundamentals of synchronization in chaotic systems,concepts,and applications[J].Chaos,1997,7(4):520.

[16] Ucar A.A prototype model for chaos studies[J].International Journal of Engineering Science,2002,40(3):251-258.

[17] Senthilkumar D V,Kurths J,Lakshmanan M.Stability of synchronization in coupled time-delay systems using Krasovskii-Lyapunov theory[J].Physical Review E,2009,79(6):1-4.

[18] Ren Hai-peng,Baptista M,Grebogi C.Wireless communication with chaos[J].Physical Review Letter,2013,110(18):1-5.