考虑尾气排放的匝道控制最优化算法研究

高万宝,邹 娇,吴 坚

(安徽科力信息产业有限公司安徽省智能交通重点实验室,合肥230088)

考虑尾气排放的匝道控制最优化算法研究

高万宝*,邹 娇,吴 坚

(安徽科力信息产业有限公司安徽省智能交通重点实验室,合肥230088)

匝道控制是缓解快速路拥堵的有效措施,而且有增加通行流量、提高运行效率、减少交通事故的功能,随着国民经济的提高,社会公众对环境污染的关注越来越高,所以研究考虑尾气排放减少的匝道控制是立足民生的课题.本文算法考虑了尾气排放因素,同时兼顾两个目标,一是减少总车辆旅行时间,二是最大量地减少尾气排放.利用Paramics仿真软件对算法进行了模拟实验,并且运用CMEM交通排放模型进行了计算,分析结果显示新算法有效地降低了总车辆旅行时间,而且比ALINEA算法更能降低匝道路段的尾气排放量和排队数,特别是在上坡坡度较大的情况下,新算法可以更多的减少尾气排放总量.

智能交通;尾气排放减少;密度控制算法;匝道信号控制;Paramics仿真

1 引 言

自20世纪70年代以来,世界各国开始了关于交通对环境影响的研究,主要集中于机动车单车排放因子的确定和交通流尾气的扩散规律,提出了许多理论模型[1],如MOBILE5、MOBILE6、VT-Micro及CMEM模型.最近流行的CMEM模型,应用效果较好,本文基于此模型开发了算法.

交通尾气排放是城市环境污染的主要来源之一,车辆所排放的废气含有多种有害物质,如二氧化碳(CO2)、一氧化碳(CO)、氮氧化物(NOx)和碳氢化合物(HC)等,因此,通过各种可能的交通管理措施来减少道路交通尾气排放非常重要.随着城市化进程的加快,汽车拥有量大幅增加,城市道路特别是匝道交口拥堵越来越严重,应对这一问题,入口匝道控制已被证明是一种灵活而有效地缓解拥堵方式.通过调节匝道交口的进入流量,车辆运行更加有序,交通流更加平缓,车辆运行也更安全.由于主线交通流畅通运行,匝道控制还有减少尾气排放的作用.

2 理论研究基础

2.1 匝道信号控制

匝道控制的理论基础是控制总车辆旅行时间消费,通过进出消费模型[2],全部车辆行驶在网络上的花费时间最小化等同于模型输出流量最大化,因此必须控制网络的交通条件,保证最大的出口流量输出.需求—容量算法是通过调节匝道进入的交通流,使其与上游流量总和不超过主干道的通行能力,从而最大限度地输出交通流[3].

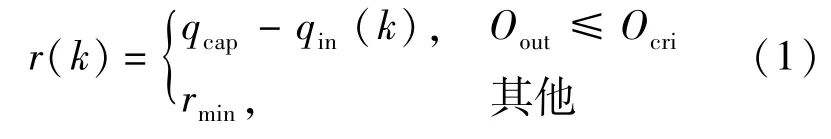
式中 r(k)为第k个周期内的入口匝道调节率, veh/h;qcap为下游的通行能力,veh/h;qin为上游进入交通流量,veh/h;rmin为最小匝道调节率,veh/h.

ALINEA算法是通过流量与占有率的关系,使快速路占有率维持在期望值附近,输出最大的下游流量,从而最优地利用快速路[4].

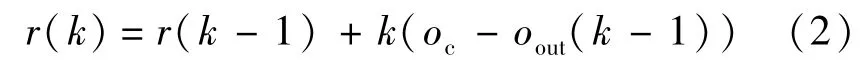
式中 k为大于0的可调参数,oc为下游路段期望占有率,oout(k-1)为第k-1个周期内下游路段的时间占有率.

2.2 匝道尾气排放

匝道控制是牺牲匝道流量来保证快速路的畅通,所以控制后匝道路段拥堵程度将会增加,因此,尾气排放由两部分组成:干线排放量和匝道排放量.

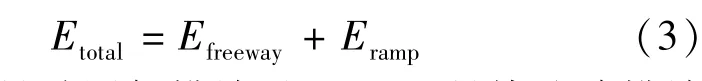
式中 Etotal是总尾气排放量;Efreeway是快速路排放量;Eramp是匝道区间排放量.

匝道信号控制运行后,快速路交通流更加快速和平稳,排放量减少.匝道路段的车辆由于受到信号灯的影响,密度增加,交通拥堵恶化,这种缓慢而且走走停停交通状况会导致更高的排放发生,因此匝道控制的尾气排放影响一般包括两个方面:主路的排放减小,匝道路段排放增加[5].

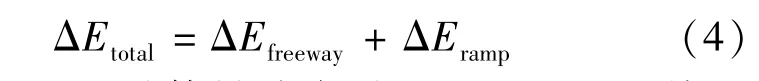
式中 ΔEtotal是总体排放净增量;ΔEfreeway是快速路排放净增量;ΔEramp是匝道路段排放净增量.

2.3 新算法概述

基于经典的交通流理论,如 Greenshield、Greenberg或Underwood模型[6],根据流量与密度的关系方程,通过控制密度可以实现交通流的最大输出.一般情况下,路段上车辆越多即车流密度越大,路段产生的尾气排放也就越多,因此,可以通过降低密度值来降低污染排放.本文算法设计了区间密度的监测方法,控制目标函数包括两个方面,一是减少路网车辆总旅行时间,二是最大限度的减少匝道排队长度,从而尽可能地减少尾气排放.

3 匝道控制优化算法研究

3.1 尾气排放研究

交通拥堵造成汽车长时间低速、怠速运行,致使污染物排放量加大.特别是匝道交汇路段,道路拥挤,车流密度较大,机动车油耗和排气污染严重.

影响机动车排放的因素很多,本文主要考虑了速度和加速度,机动车在路上行驶,随着车速和负载的变化,各种污染物的排放量也在随时变化.

汽车发动机燃烧排放过程是一个复杂的过程, CO,HC和NOx三种污染物的生成条件不同,一般情况下随着速度的增加,HC的综合排放是逐渐减少,CO的综合排放是逐渐减少,NOx的排放呈现先逐渐减少后逐渐增加的趋势.

加速时,进气量和供油量都随之增大,CO排放浓度呈下降趋势,而未完全燃烧的燃料会直接排出,造成了HC排放浓度的增加;同时,燃烧温度迅速提高,燃烧室内有充足的氧气和氮气来参加反应,造成高浓度的NOx生成.

3.2 密度测量方法研究

交通密度表示单位区间长度上存在的车辆个数,本文 使用 了 进 出 计 数 法 (Input-Output Counting)来测定,只需实时检测路段区间内初期存在的车辆个数、进入区间的车辆个数和离开区间的车辆个数,如图1所示.

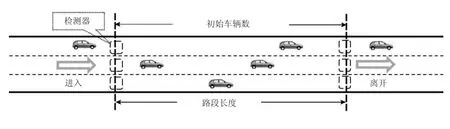
图1 进出计数法Fig.1 Input-output counting method

通过进出计数法,结合式(5)、式(6)可以计算实时的区间密度值.

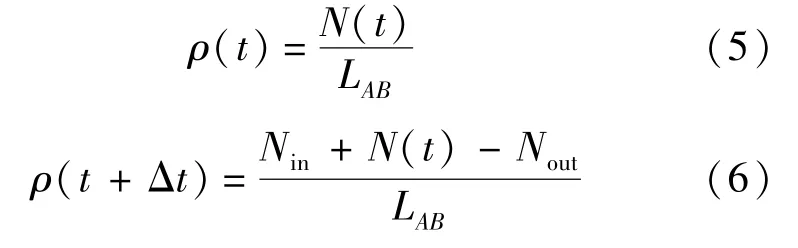
式中 Δt为单位时间演变步长;ρ(t+Δt)为t+ Δt时刻的区间密度;Nin为统计时间间隔内进入区间的车辆数;N(t)为区间t时刻存在的车辆数;Nout为统计时间间隔内离开区间的车辆数;LAB为区间AB的长度.

根据累计车辆个数,密度算法可以简化为式(7),定义初始上游检测器上累积的车辆个数等于区间初期存在车辆数[7],即QA(t0)=Inv(t0).

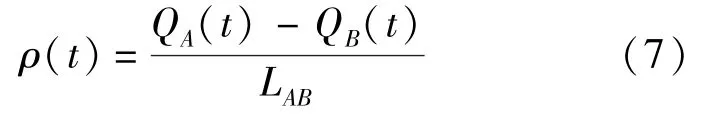
式中 QA(t)为上游检测点t时刻的累积车辆数; QB(t)为下游检测点t时刻的累积车辆数.

累积计数方法的概念如图2所示.

为了精确测量实时的密度值,初期存在车辆个数非常重要,很多方法可以测量初期存在的车辆个数,如浮动车辆法、车辆牌照检测法、摄像拍照法等.浮动车辆法[8]:定义区间AB两点,当浮动车经过A点时,A点的检测器开始计数经过的车辆数NA,此时浮动车由A点开始向B点移动,移动过程中记录浮动车超车个数NO及被超车个数NP,当浮动车到达 B点时,初期存在车辆个数处理过程完毕.

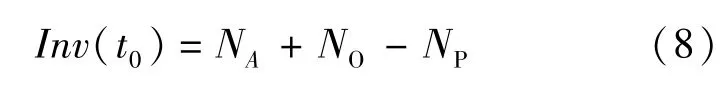
这里的路段AB定义为几何条件保持一致的道路区段,中间没有车辆流失与增加的断口,保持车辆的守恒,适用于快速路和高速路段,城市道路需要两个交叉口中间选取.路段AB间车辆运行的时间位置关系如图3所示,浮动车辆由A到达B的时间t0为初期存在车辆个数的处理时间.

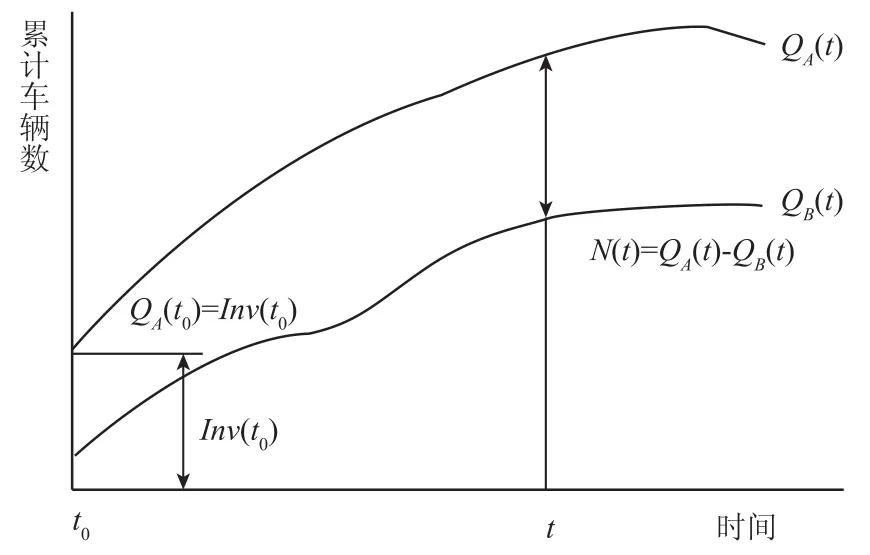
图2 累积计数方法的概念Fig.2 Conceptual representation of cumulative counting method

通过对合肥长江西路高架(潜山路—陈村路)路段浮动车实验,对早高峰(7:00-9:00)、平峰(10:00-12:00)、晚高峰(17:00-19:00)的交通流分别进行检测,由上述算法得到初期存在个数,并与视频录像进行对比得出算法的准确度.

检测器实时采集交通流数据,匝道入口的信号灯信号控制参数说明如表2所示.

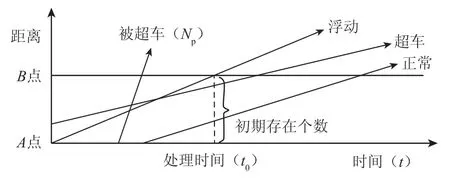
图3 初期存在个数算法描述Fig.3 Initial vehicles counting algorithm description

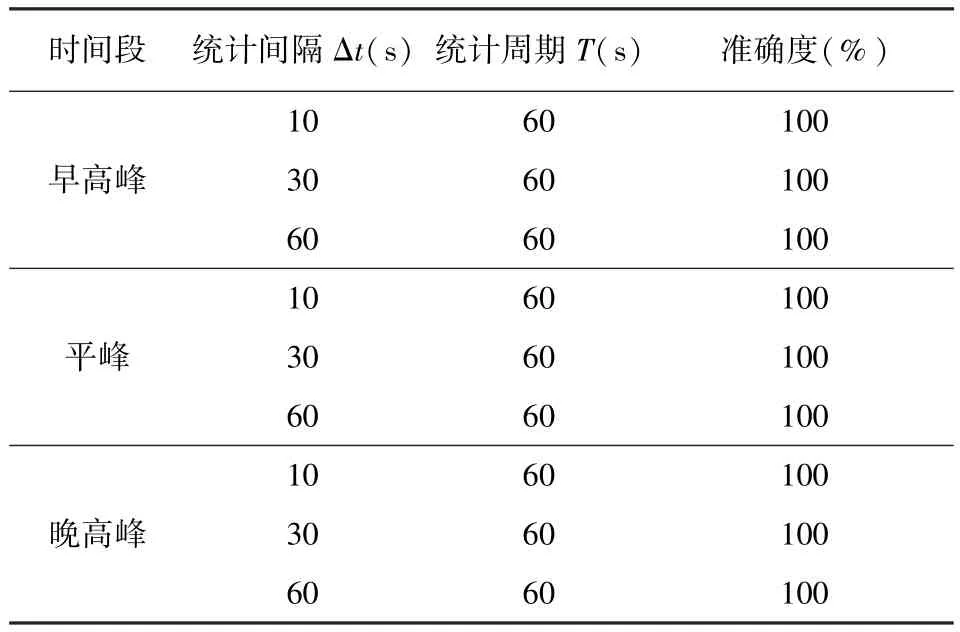
表1 初期存在个数算法的效果Table 1 Benefit of initial vehicles counting algorithm

表2 参数符号定义Table 2 Definition of the symbols

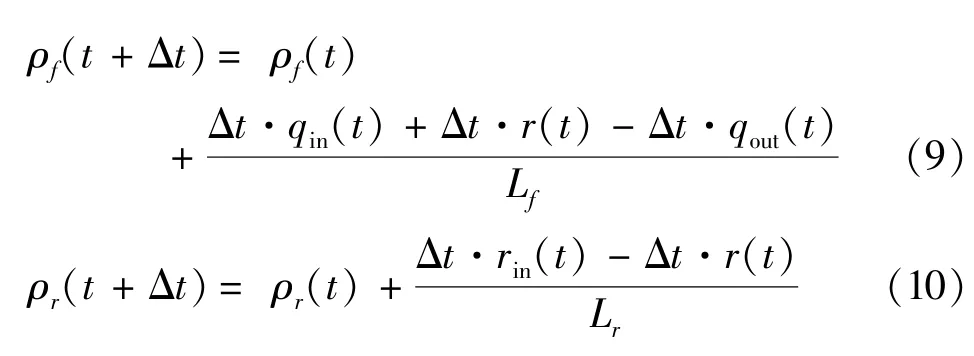
图4描绘了一个基本的入口匝道模型,以及检测器埋设位置,匝道入口设置信号灯,利用式(5)和式(6)可以分别得到快速路和匝道的实时交通流密度ρf和ρr.

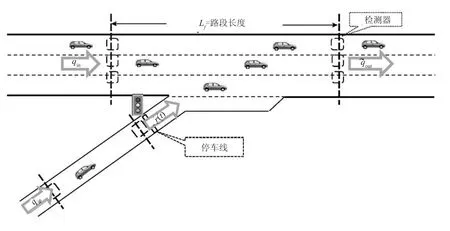
图4 单个入口匝道模型和检测器Fig.4 Isolated on-ramp model and detectors

3.3 最优控制算法研究

新算法的目标是保持干线交通流密度在期望值附近,同时尽可能地减小排队数,所以要定义目标函数,通过控制函数的动态变化来实现预期的效果.

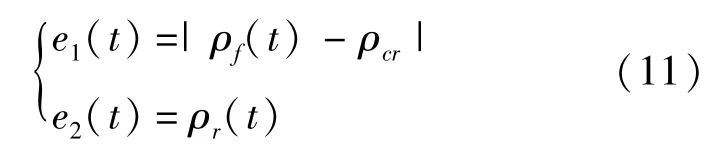
式中 e1(t)和e2(t)为误差控制目标函数;ρcr为干线路段最优密度值.

动态减少e(t)值,干线密度就会靠近期望值,排队长度也会越来越小,所以建立可以使e(t)不断变小的控制方程.定义式(12),其中k＞0,解式(12)得到式(13),说明经过t时间后e(t)会变得更小,体现了负指数函数的性质[9].

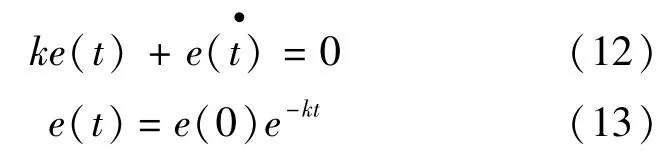
为了求解式(12),首先要求解e(t)的导数,同时要精确的计算区间交通流密度.求导式(11),得到式(14).

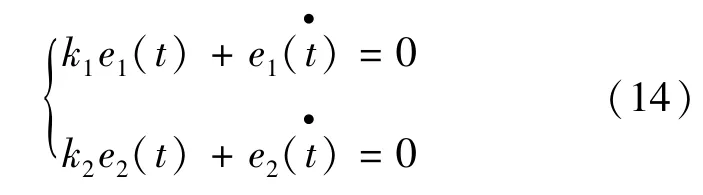
式中 k1和k2分别为误差控制目标函数e1(t)和e2(t)的系数.

经过Δt的时间间隔,即时刻由t到了t+Δt,更新后的区间密度值可以利用式(9)或式(10)得出,当然要先检测区间已经存在的车辆数和进出区间的车辆个数,移项转换同时除以Δt,可以得到

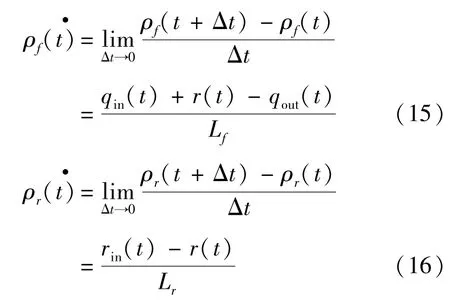
求解式(15)和式(16)可以得到

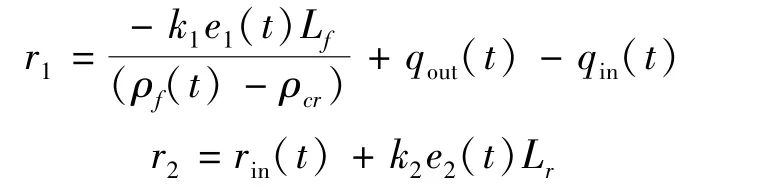
匝道调节率是关于(r1,r2)的函数方程,当主路需求调节率大于匝道需求调节率时,取匝道调节率为r1;否则,取r1和r2的加权值,加权系数根据匝道的密度实时变化,新算法如式(17).

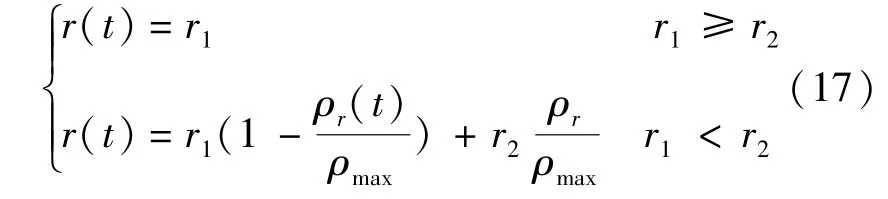
算法中未知的变量只有 qin,qout,rin,Δt,ρf(t)与ρr(t),只要实时的检测这些参数,就可以优化控制交通流运行环境,增加下游流量并减小尾气排放.

4 PARAMICS仿真实验

通过微观交通仿真软件,可以在进行工程施工前,利用很少的费用就能对工程前后的效果进行评价.对新匝道控制算法进行仿真,利用无信号控制、ALINEA算法和实时密度算法,编译生成plugin.dll文件,控制匝道信号,调节路网的交通条件.实验分成三个场景,匝道的坡度不同,为正切值0,0.04和0.08.

利用CMEM尾气排放模型,将路网模拟运行的参数转化为尾气排放数据,需要设置的是车辆的种类与比例,车辆的状态,以及污染气体的种类,如图5所示.

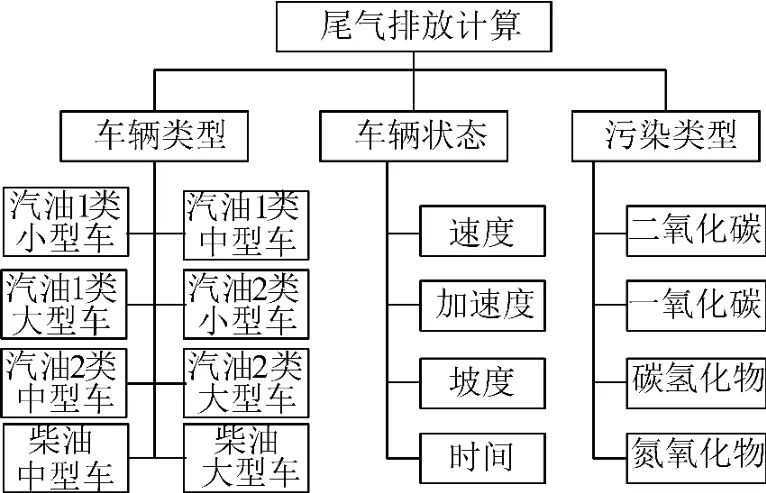
图5 尾气排放计算流程图Fig.5 Diagram of emission calculation

式中 C表示信号的周期时间长度;G表示有效绿色时间;s是匝道通行饱和流量.

信号的周期长度通过式(19)进行计算.

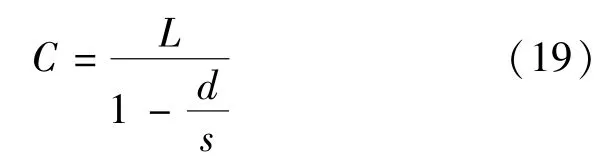
匝道绿灯调节时间通过式(18)进行计算.

式中 L为损失时间,灯色切换过程中的损失时间和不能被充分利用的绿灯时间;d是车辆到达率,与交通服务水平有关,模拟实验条件分服务水平C、F和C-F-C三种情况.表3设定了各个实验参数的初值.

每次模拟实验输出快速路的密度(vehicles/ km/lane),匝道的排队长度(vehicles),总车辆旅行时间(vehicles·second),下游交通流量(vehicles/ hour)的数据,以及干路与匝道路段的尾气排放量(g)数据.考虑到不同的交通条件与交通流分布情况,模拟实验选取了10个种子(种子是仿真软件的一个参数,不同的值代表不同的交通流分布情况),即每项实验都进行了10次模拟,所以可以利用T-test进行数理统计分析.

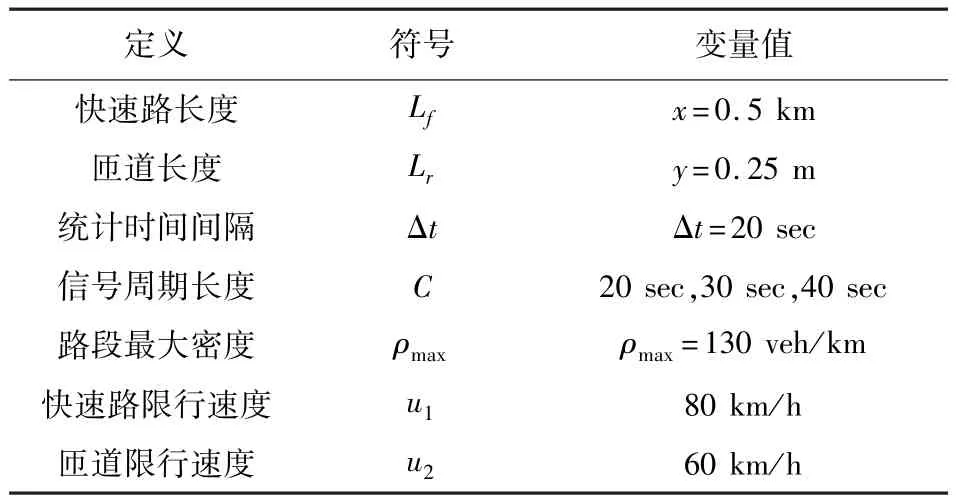
表3 参数初值设定Table 3 Parameters'pre-set value

4 实验结果分析

区间密度进出计数法和基于实时密度的匝道控制算法都进行了编译,ALINEA算法和无信号控制也在同样的交通环境下模拟,与无信号控制进行了效果比较,进而进行相应的评价.各个实验的结果如表4所示.

条件假设:

H0:两种匝道控制策略实施的效果数据是相等的;

Ha:两种匝道控制策略实施的效果数据是一个方案大于另一个方案y1-y2＞0.

分析结果显示ALINEA算法和密度控制算法都降低了路网总车辆旅行时间,在95%的信赖区间上无法证明ALINEA算法和密度控制算法的优劣,还需要继续研究.

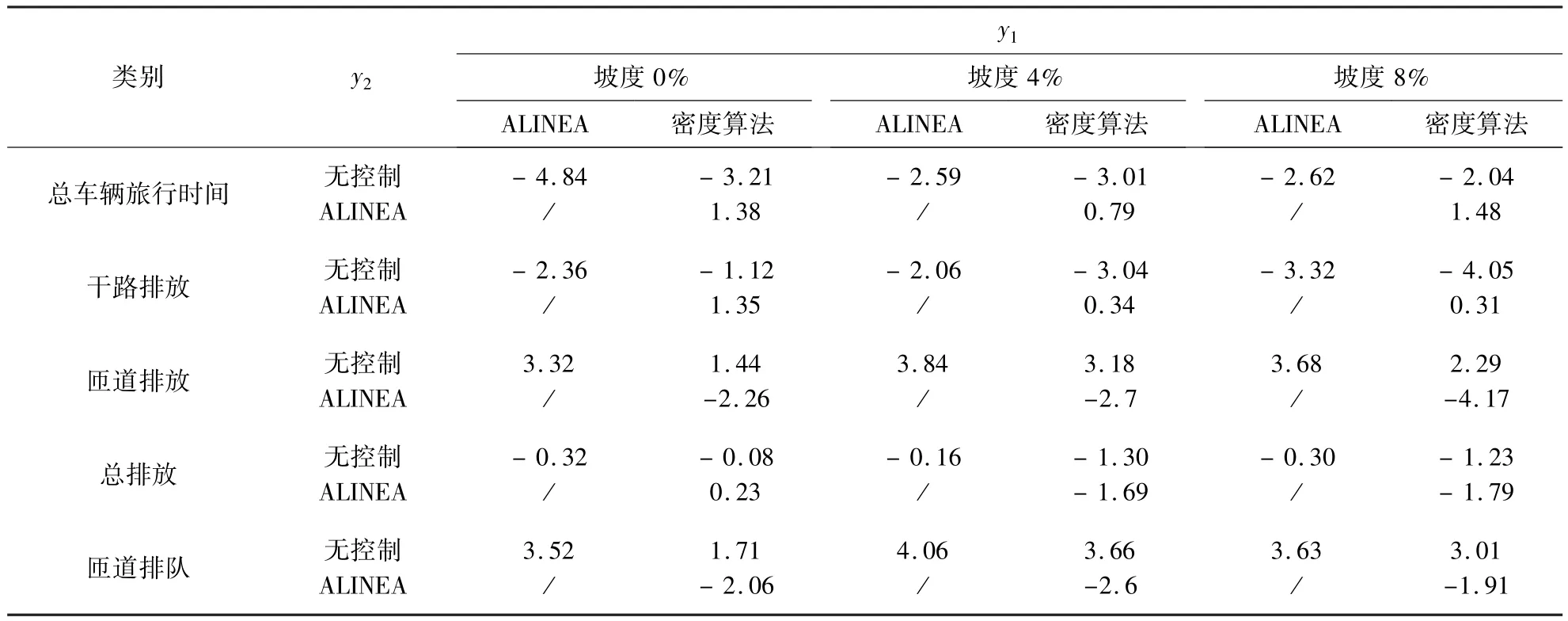
表4 各种算法的效果Table 4 Benefit for each control algorithm

ALINEA算法和密度控制策略与无信号控制相比,都可以减少快速路的尾气排放量,但是无法证明ALINEA算法和密度算法的优劣.

ALINEA算法和密度控制策略与无信号控制相比,都增加了匝道路段的尾气排放量和排队长度,同时密度算法比ALINEA算法更能减少尾气排放和匝道排队长度.

尾气排放总量方面,统计结果无法证明匝道控制的效果,虽然干路的排气排放减少、匝道路段尾气排放增加,但是两者的总和的净增量还是一个不确定的值;同时,当匝道坡度增加时,密度控制算法优于ALINEA算法.

分析原因,匝道控制实施后,匝道路段的车辆受到信号灯的控制,排队长度增加拥堵加剧,这种缓慢而且走走停停的交通流状况会导致更高的尾气排放量.到匝道坡度增加时影响程度增大,密度控制策略会适当的增加匝道的流量,而ALINEA算法无视这种现象,导致更多的排放和排队数.

5 研究结论

本文设计的算法能够减少路网总车辆旅行时间,减少匝道排队数,减少尾气排放量,缓解交通拥堵.新算法和ALINEA算法都减少路网总车辆旅行时间,增加了匝道路段的排队数;两种算法都可以减少主干路的排放量,增加匝道路段的排放值.另外,新算法比ALINEA算法更能有效地减少匝道排队长度和尾气排放量,当匝道坡度增加时,新算法的尾气排放总量小于ALINEA算法,坡度越大效果越佳.

密度算法适用与中等服务水平的交通流条件,不足之处是没有考虑车辆长度对实验的影响,所有的车辆都规定了统一的长度,与现实有一定的误差;另外信号控制周期长度的计算也需提出新的优化算法及各种周期长度下的效果比较,增加算法的准确度.

[1]Rakha H,Ahn K,Trani A.Comparison of mobile5a, mobileE6, VT-mobile, and CMEM models for estimating hot-stabilized light-duty gasoline vehicle emissions[J].Canadian Journal of Civil Engineering, 2003(30):1010.

[2]Papageorgiou M,Hadj-Salem H,Blosseville J M. ALINEA:A local feedback control law for on-ramp metering[J].Transportation Research Record,1991: 58-64.

[3]Papageorgiou M,Salem H,Middleham F.ALINEA local ramp metering: Summary offield results[J]. Transportation Research Record, 1997(1603): 90-98.

[4]Papageorgiou M,Kotsialos A.Freeway ramp metering: An overview[J].IEEE Transactions on Intelligent Transportation Systems,2002,3(4):271-281.

[5]Kang S,Gillen D.Assessing the benefits and costs of intelligent transportation systems:Ramp meters[R]. California PATH Program,Working paper UCB-ITSPRR-99-19,1999.

[6]Adolf D M.Traffic flow fundamentals[M].Prentice Hall, 1990:160-226.

[7]Lee C W,Lee J B,Lee M S.Density measurement algorithm for freeway segment using rwo point setectors [J].Journal of Advanced Transportation Engineering, 2011(45):207-218.

[8]高万宝,吴坚,邹娇.基于实时密度的入口匝道控制算法研究[J].交通运输系统工程与信息,2012,12 (2):150-156.[GAO W B,WU J,ZOU J.Real-time density based on-ramp metering algorithm study[J]. Journal of Transportation Systems Engineering and Information Technology,2012,12(2):150-156.]

[9]OzbayK, YasarL, Kachroo P. Comprehensive evaluation of feedback-based freeway ramp-metering strategy by using microscopic simulation-taking ramp queues into account[J]. Transportation Research Board,2004(1867):89-96.

Emission-Based Optimization Algorithm for Ramp Metering

GAO Wan-bao,ZOU Jiao,WU Jian
(Anhui Key Laboratory of ITS,Anhui Keli Information Industry CO.LTD,Hefei 230088,China)

Ramp metering is an effective way to alleviate freeway congestion.It also makes some contributions to increase traffic flow,improve operational efficiency,and reduce traffic accidents,etc.With the rapid growth of the national economy,the public concerns more on the increasing environmental pollution.The study on ramp control considering emissions reduction is an important issue related to people's livelihood.The algorithm in the paper considers some emissions factor.It occupies two objectives, the primary is to minimize total vehicle travel time,and the other is to reduce ramp emission as much as possible.The PARAMICS simulation program is used to evaluate its performance comparing with the ALINEA and no metering condition,and the CMEM traffic emission model is used to calculate the result. Analysis shows that the new ramp metering algorithm is effective in reducing the total vehicle travel time,as well as significantly reducing on-ramp emissions and queues than the ALINEA strategy.Especially,on the large uphill gradient condition,new algorithm could reduce much more total emission.

intelligent transportation;emission reduction;density control algorithm;ramp signal control; Paramics simulation

U491

A

U491

A

1009-6744(2013)01-0156-07

2012-06-13

2012-11-09录用日期:2012-11-20

工信部电子信息产业基金(工信部财[2010]301).

高万宝(1984-),男,安徽凤阳人,研究员.

*通讯作者:gaowanbao2005@hotmail.com