基于多项式样条的中国利率期限结构实证研究

沈 磊

（安徽财经大学 金融学院，安徽 蚌埠 233000）

1 引言

利率期限结构是指在相同的风险水平下，利率与剩余到期期限之间的数量关系，也就是理论上零息票债券即期收益率曲线.利率风险是投资者面临的一个重要风险，通过对市场利率期限结构的分析可以发现并利用市场上资产定价的不合理性进行套利，获取无风险收益.在宏观经济领域，可以利用利率期限结构预测宏观经济变量的变动，判断未来经济走势.而完善和准确的期限结构是一个国家金融市场中固定收益证券定价的基本工具.因此，利率期限结构理论在宏观经济管理、资产定价、保值和风险管理以及套利和投资等领域都有非常广泛的应用，对于开发新型金融产品、进行金融创新也有着重要而积极的作用.它是资产定价、套期保值、金融产品设计、套利以及投资等的基础，对利率期限结构的研究一直是金融学中一个重要而又基本的课题.而国债利率期限结构又是所有利率期限结构研究的基础，它在经济及金融分析中有着非常重要的作用.研究国债利率期限结构可以为我国利率市场化进程提供基准利率支持，对它的相应的研究可以化解汇率风险，增加金融系统的稳定性，为我国的资产定价提供一个坚实的理论依据，促进我国资本市场的不断完善.因此，对于国债利率期限结构的研究是非常重要也是很有意义的.

McCulloh最先提出将多项式样条函数运用于利率期限结构中，采取某种形式的多项式样条函数来拟合贴现函数，再通过参数估计法得到样条函数中的各个待定参数，并提出二次和三次多项式是最有效的多项式样条函数的观点；丘菀华和周荣喜利用多项式样条函数构造出了我国国债的利率期限结构；王晓芳，刘凤根，韩龙论证了多项式样条函数不会限制贴现函数的形式，具有较好的适应性；郭多祚，刘琳琳认为三次多项式样条函数在估计利率期限结构时具有贴切原始数据的优势.因为二次以上的多项式样条函数是二次可微的，一阶导是连续的，比线性插值函数具有更好的数学特征，因此在拟合向上的收益率曲线时与实际观察到的向上凸的弧线更为相似.

2 研究思路与方法

估计利率期限的研究可以分为：一般均衡模型分析、无套利均衡分析和曲线模拟分析，前二者属于动态模型法，比较有影响力的有 VASICEK、CIR（Cox、Ingersoll和 Ross）、Holl等模型；曲线拟合法一般假设一种利率函数或者贴现函数，利用选取的国债某一横截面数据以及参数估计法，得出假设函数的系数，使之与主干点拟合，从而估计利率期限结构曲线.假设的函数可以是多项式样条函数、B样条函数、指数样条函数、无节点样条函数等.本文基于多项式样条函数拟合利率函数得出连续收益率曲线并进行实证分析，这是一种对利率期限结构的静态分析，利用的是某一横截面上的数据，而不是时间序列.通过这种静态的分析我们可以得到某一时点上的即期利率与剩余期限之间的关系，使我们对我国国债市场有进一步的了解，有针对性的对我国国债市场的改革和发展提出相应的看法和建议.

2.1 利用付息债券收益率推导无息债券的即期收益率

由于我国市场中普遍存在的是付息债券，零息债券很少见，因而我们不能通过市场公布的相关数据直接观察到一条完整的国债即期收益率的期限结构，只能通过借助付息债券间接估计.

2.1.1 连续复利的情况

假设某一付息国债I是连续复利的，其到期时间为T，每期支付利息Ci，债券面值Mi，从当前到t时刻的到期收益率或者贴现率是ri，则该付息国债的理论价格为：

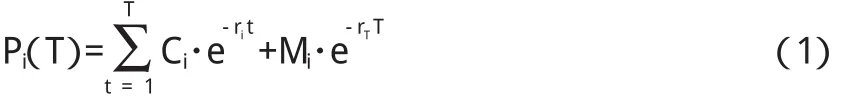
如果我们假设贴现函数的表达式为F(t)，则（1）式可以写成：

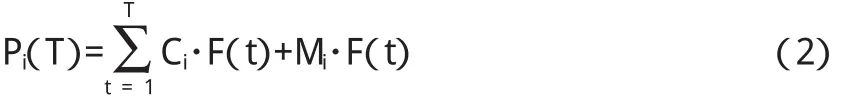
F(t)是时间t的函数，利用该债券某一横截面数据，将相应的债券价格、付息额、债券面值、剩余偿还期限代入（2）式，利用线性回归和最小二乘法估计贴现函数中的参数，得出贴现函数的具体形式，进而得到即期利率R(t)即该债券的理论即期收益率.

2.1.2 分期支付利息的情况

建立年付息一次的固定利息国债的理论价格和即期利率之间的模型关系：

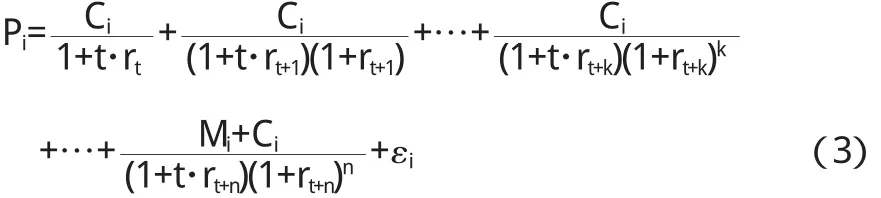
Ci是该i种固定付息债券每次支付的利息；Pi是该债券的全价；rt+k为t+k时刻的即期利率；t为样本观测日到下一个付息日之间的时间间隔；Mi为债券票面金额.

由于贴现函数F(t+k)与即期利率rt+k之间的的关系是：

所以（3）式可以写成：

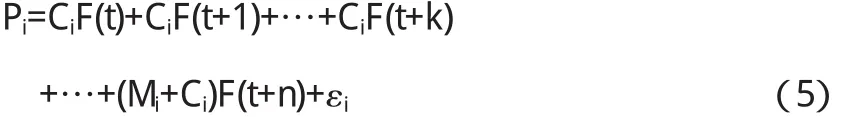
在利用分段多项式样条函数来代替贴现函数F(t)时，如果我们进行分段的话，就可以利用（5）式得到不同的贴现函数.用最小二乘法对这些分段方程进行线性回归，从而得出各个分段样条函数的系数.从而计算出即期收益率或者即期利率.

2.2 样条贴现函数的选择

2.2.1 数学理论的支持

根据魏尔斯特拉斯逼近定理（Weierstrass Approximation Theorem）:一个连续的函数可以由一组函数近似地逼近.根据这个理论，我们用一组以到期日t为变量的样条函数来近似表示贴现函数，然后通过使样本债券的理论价格与市场的实际价格差别（方差）最小化的线性回归，得到参数估计，进而得到以年利率为单位的贴现函数R(t)的估计方程：

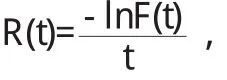
据此便可得到关于时间和利率的债券利率期限结构.

2.2.2 多项式样条次幂以及多项式样条的数量决定

我们在利用多项式样条函数逼近贴现函数的时候，理论上可以使用的有二次样条、三次样条、四次、五次乃至更高次的样条函数，但是在实际操作中，为了保证拟合的光滑性，一般需要要求样条函数在每个节点的一阶导数相等和样条函数在每个节点的二阶导数相等.McCulloch提出二次、三次多项式样条函数来对贴现函数进行拟合，他认为二次样条函数间接拟合利率期限结构会产生一个不光滑的远期利率曲线，F(t)的二阶导数是离散的，因此它的曲线不光滑.为了得到一个光滑的即期利率曲线，必须用至少一个三次样条函数去拟合贴现函数，而当多项式的基函数阶数大于三阶时，模型比较复杂，验证导数的连续性有困难，阶数越高困难越大.我们采用的便是三次多项式样条函数，形式为：

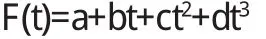
在多项式样条函数的数量方面，由于样条函数的数量决定了拟合程度和光滑程度.如果增加样条函数的数量，拟合程度会越好，但是节点就会比较多，拟合曲线就不会光滑.我国利率市场交易品种数量少，一般可以选择3个样条函数.

3 实证应用和分析

3.1 数据和样条函数的选取

在我国研究利率期限结构大多用的是能反应市场的国债利率或者回购利率，其他的譬如商业银行的贷款利率、银行间的拆借利率由于中央银行的政策性规定，利率变化幅度小，不能反应真正的市场利率.其次，国债交易市场有银行间的交易市场与交易所市场，这两个市场相互独立，其中银行间国债市场主要用于提供提债券市场的信息服务等，交易并不活跃，单笔交易数量大，不利于正常反应市场需求情况，因此我们选取上海证券交易所的国债及其回购品种作为研究对象.

鉴于我国目前并不完善的利率、货币等各项传导机制，对于交易所的长期国债而言，到期期限较长，其价格受到利率、通货膨胀等因素的影响较大，从而导致其价格被低估，价格偏低.因此在挑选债券时，我们将剩余期限在10年以上的国债排除在外.并将0到10年到期的国债分为三段：第一段是0～2年；第二段是2～5年；第三段是5～10年，这样分成三段的多项式样条函数可以写成：

3.2 模型的变化和软件的应用

为了保证三次多项式样条函数的拟合程度和光滑程度，函数F(t)必须满足函数平滑性和可导性约束条件，结合（6）式我们可以将相互独立的参数进一步缩减，整理后可得下式：

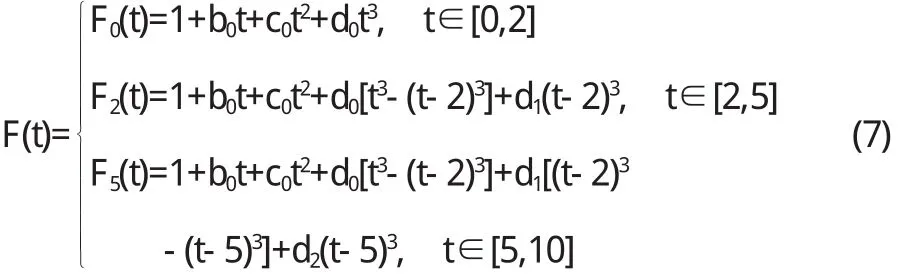
将债券价格、息票额的数值和贴现函数的各具体形式代入（7）和（2），得到一个含有5个参数的多元线性回归模型.

为便于方程的计算，我们设定：所有债券的假定剩余到期时间为9至10年，9年以下的债券在最后一次付息还本以后的付息日付息额均为零，这样既不与实际相违背，也方便模型的简便化.因此多元线性回归模型的通式右侧仍然是债券价格，左侧是上面10个公式的加总，合并同类项得到：

其中，A=Ci1+Ci2+…+Ci10；

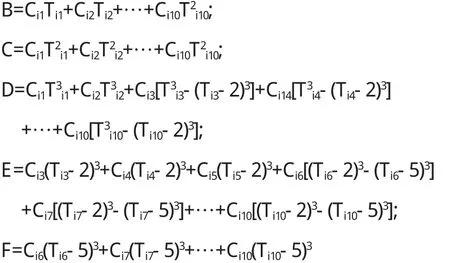
设定目标函数为：

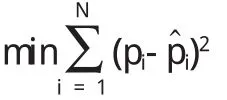
利用线性最小二乘法估计出贴现函数F(t)的各个参数，最后利用公式（3）将贴现率转化成连续复利的零息票国债的到期收益率，得出国债利率期限结构，作图画出利率期限结构曲线.

3.3 实证分析

本文选取2010年4月14日上海证券交易所的国债交易价格为研究对象对我国的利率期限结构进行实证分析.由于我国的上市国债种类和数目较多，为方便计算，我们要求选取的付息债券每年只付息一次，在到期日支付票面本金和最后一笔利息，并且在存续期间内债券正常付息.在某日上市的交易所付息国债中选取10只国债的交易数据（包括全价，到期期限，到期收益率等信息）作为样本（见表1），对我国的国债收益率曲线进行拟合.

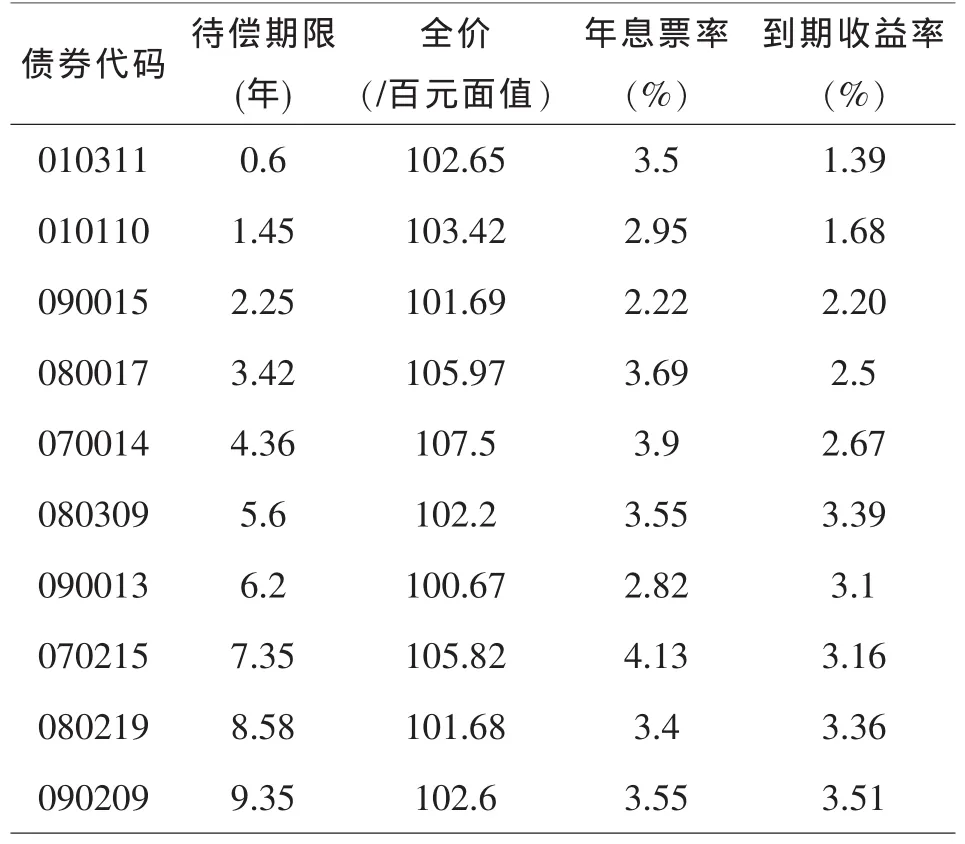
表1 上海证券交易所国债交易情况（2010-04-14）

首先，将交易数据代入贴现函数可以得到回归样本，然后通过Eviews软件，利用线性最小二乘法估计出参数b0,c0,d0,d1,d2和相关标准差，以及F检验值，相关结果如表2所示.由计算结果中F检验值大小可知回归模型的通过整体显著性检验，由修正R2的数值可以看出，模型拟合优度较高，总体效果是比较好的，因此，模型有效，可以用来进行分析研究.

表2 多项式样条函数参数估计结果

于是，将所得的参数估计结果代入（6）式，我们就可以得到贴现函数的逼近函数具体表达式为:

再根据公式（3）我们将F(t)转化成连续复利的零息票国债的到期收益率R(t)，将t设为1～10的间隔为0.5的年限，可得R(t)如表3所示.

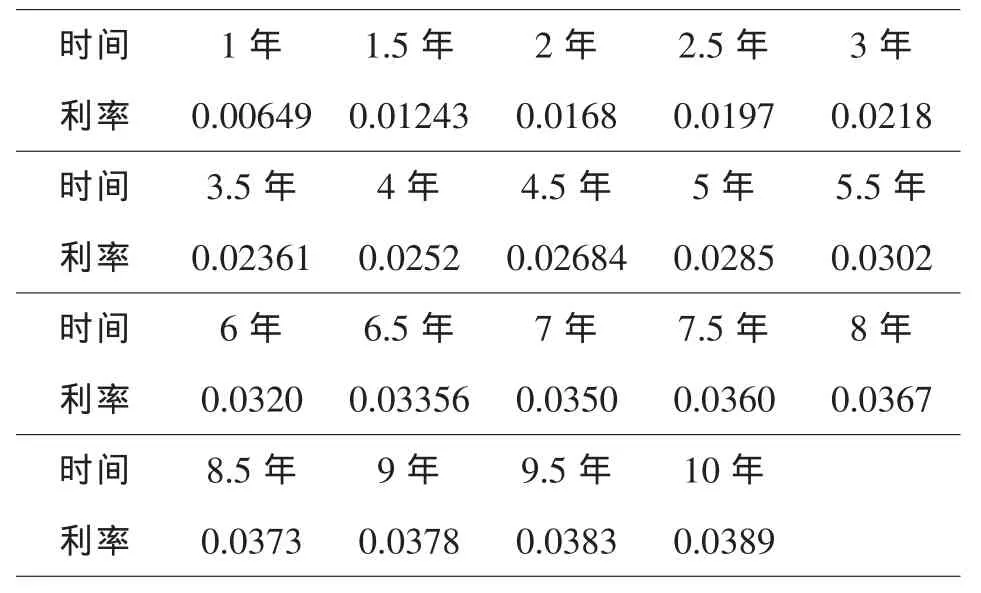
表3 国债拟合收益率汇总

由以上数据，可以做出即期利率期限结构的曲线（如图2所示）.可以看出，拟合出来的国债收益率曲线较平滑，由计算结果知其拟合优度较好，可以认为采用三次多项式样条函数估计我国国债利率期限结构曲线是有效的.这种简便可行的方法能够很好的拟合我们得到的数据，可以刻画出性质良好的率期限结构曲线.当我们研究利率期限结构曲线的特点和基本形状并据此来预测未来利率变化趋势的时候，这种研究方法颇为适宜.

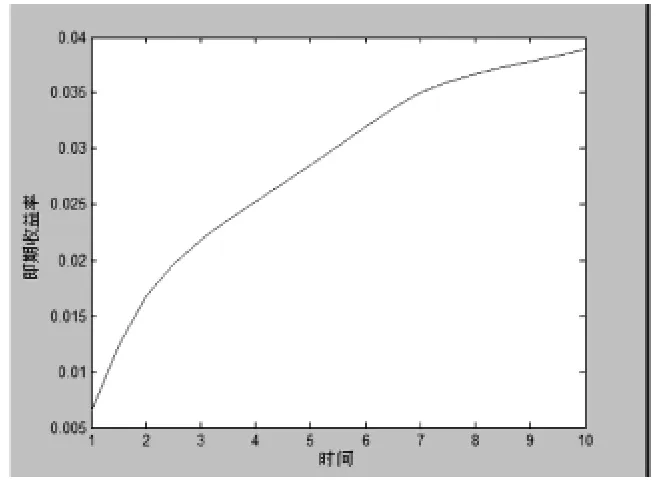
图1 上交所国债利率期限结构曲线（2010年04月14日）

4 结论

从以上对利率期限结构的估计中我们得到一些有关我国利率期限结构方面的结论.

4.1 以上对利率期限结构的估计中，是利用多项式样条函数构造国债利率期限结构的一种静态的分析，是立足于某一时点的国债收益与期限的关系.

4.2 利用多项式样条函数可以得到一条光滑的利率期限结构曲线，然而我们将这个多项式分成三段后，拟合程度可达到90%以上，并且分段式样条函数得到的利率期限结构在长期趋于稳定，与实际情况吻合.

4.3 在用多项式样条函数构造利率期限结构时，需要把握好拟合尺度，视用途分情况而定.次幂的选择和分段的选取要尽量做到贴切实际.

4.4 总体来说，我国国债利率期限结构是向右上方倾斜的，这说明投资的期限越长，收益率越高，这一点符合资金的时间价值理论.短中期利率较低，长期利率保持快速增长、低通胀的良好状况.市场资金较为宽松，中短期利率较低.

4.5 随着中国利率市场化改革的迅速推进以及国债市场的进一步发展，国债交易品种和交易规模的不断丰富和扩大，以及中国金融市场的全面开放，进行动态模型的研究、实证和应用会是今后的主要研究方向.

〔1〕刘灿，易路.沪深两市国债收益率期限结构的实证研究[J].证券市场导报，2004（2）：38.

〔2〕朱峰.国债即期利率期限结构的拟合估计[J].证券市场导报，2003（4）：31.

〔3〕王晓芳，刘凤根，韩龙.基于三次样条函数的中国国债利率期限结构的曲线构造[J].系统工程，2004（4）：85-88.

〔4〕周荣喜，邱菀华.基于多项式样条函数的利率期限结构模型实证比较[J].系统工程，2006(4)：30-33.

〔5〕郭多祚，刘琳琳.三次多项式样条函数在国债利率期限结构研究中的应用[J].内蒙古财经学院学报，2006(4)：53-55.

〔6〕何启志，何建敏，陈姗姗.利率期限结构指数样条模型实证研究[J].管理科学，2008(1)：100-103.

〔7〕洪永淼，林海.中国市场利率动态研究——基于短期国债回购利率的实证分析[J].经济学季刊，2006(5)：1-4.

〔8〕吴丹，谢赤.利率期限结构的样条估计模型及其实证研究[J].系统工程，2005(1)：54-57.