基于C#的嵌套系数法大地主题反解研究

尹文亭， 徐昌荣

（江西理工大学建筑与测绘工程学院，江西赣州341000 ）

0 引 言

椭球面上点的大地经度L、大地纬度B，两点间大地线长度S 及其正、反大地方位角A12、A21，通称为大地元素. 如果知道某些大地元素推求另一些大地元素[1-2]，这样的计算叫大地主题解算. 大地主题解算被应用于空间技术、航空、航海、国防等很多方面， 但在实际使用时会遇到各种各样的问题，为了使这些问题得以解决，长期以来，国内外众多学者一直关注该问题并提出多种解算方法[3]，大致归纳为五类[4]：①以大地线在大地坐标系中的微分方程为基础，如史赖伯公式——该公式已被广泛采用，被公认为解算短距离( 小于120 km) 大地主题的最好方法[5]，高斯平均引数法[1-2]等；②以白塞尔大地投影为基础，如陈俊勇公式[6]、张志新公式[7]，以及史国友研究的贝塞尔大地主题正解[8]和反解[9]的改进算法等； ③利用地图投影理论解算大地问题，如博林公式、巴乌曼公式、许厚泽公式[10]等；④对大地线微分方程进行数值积分的解法[11]，如高斯法、龙格-库塔法、牛顿法、嵌套系数法和切比雪夫法[1,2]等；⑤依据大地线以外其他线为基础，如弦线、法截线[1-2]等. 有关大地主题解算方法虽然比较完善，但这些方法仍然存在一些缺陷，比如说奇异问题和繁琐公式的计算，特别是应用范围受到一定的限制[13].

电脑的广泛应用，为改进大地主题的解算方法提供了新的条件. 在电算中进行迭代， 简而易行.如今嵌套系数法[14-15]大地主题解算被认为能解决任意距离的大地主题解算问题，嵌套式的解算模型更宜编制电算程序， 但是在应用嵌套系数法进行C#程序设计解算大地主题计算时发现，当大地线的起终点在同一纬度时， 某些情况反解不能解算出结果. 由于嵌套系数法大地主题解算计算公式的复杂性和问题的隐秘性，使得它很难发现.

针对上面的问题，文中提出了用倍角公式变换的方法对反解公式进行改进，改进后方法不但可以解决嵌套系数法反解的问题，而且满足精度要求.

1 嵌套系数法大地主题解算的基本原理

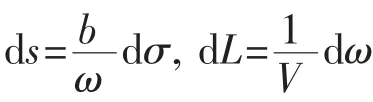
2 嵌套系数法大地主题的反解公式及问题

如果已知两点的大地坐标（L1,B1）和（L2,B2），计算两点间的大地线长S 及其正、反方位角A12、A21，这类问题叫做大地主题反解. 嵌套系数法的大地主题反解公式[2]如下：

（1） tanu1=(1-α)tan B1, tanu2=(1-α)tan B2

（2） △ω=L2-L1+d△ω 首次取d△ω

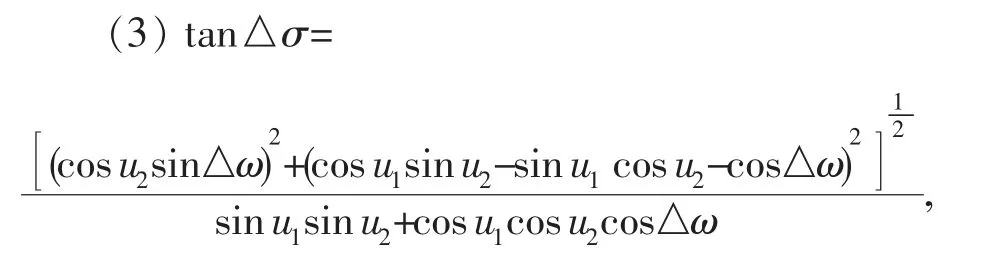
（4） cosun=cosu1cosu2sin△ω/sin△σ

（5） cos2σm=cos△σ-2sinu1sinu2/sin2un

（8） △s=K1b(△σ-d△σ)

（10）检验差：H=cosu1sinA1-cosu2sinA2

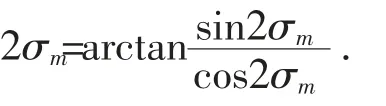
当B1≠B2时， 公式有1≥cos2σm≥-1， 此时sin≥2σm和2σm可以求出，cos4σm和cos6σm也可以解出；但是当B1=B2时， 一些情况下cos2σm＜-1， 这样就导致sin2σm和2σm解算不出来，从而导致cos4σm和cos6σm都不能解算，最终导致这时的反解计算不能解算出结果.

3 嵌套系数法反解公式的改进算法

鉴于嵌套系数法大地主题反解出现的问题，再次对公式进行数学分析，分析发现出现该问题的主要原因是计算中公式迭代导致cos2σm＜-1 而无法求解cos4σm和cos6σm的值.为了解决这个问题，通过不断地探索最后发现可以不求公式中的sin2σm和2σm，转而通过用倍角公式变换对原公式进行改化来求cos4σm和cos6σm，具体如下：

4 算例和结果分析

为了验证改进后方法是否真正解决了嵌套系数法反解中存在的问题，现以VS2010[16]为开发环境，用原嵌套系数法和改进后方法编制一套大地主题解算程序，在编写程序中参考文献[17]中注意的问题，验证时加入了高斯平均引数法和白塞尔法进行对比. 反解计算的前四个例子选用克拉索夫斯基椭球， 椭球参数为：a =6378245.0 m，b =6356863.0188 m； 最后一个算例选用1975 年国际椭球， 椭球参数为：a =6378140.0 m，b =6356755.288158 m.例1 结果见表1， 例2～例5 的起算数据见表2，结果见表3.

例1（B1=40°02′35.6784″，L1=130°10′12.2627″，B2=40°02′35.6784″，L2=128°59′53.8816″）

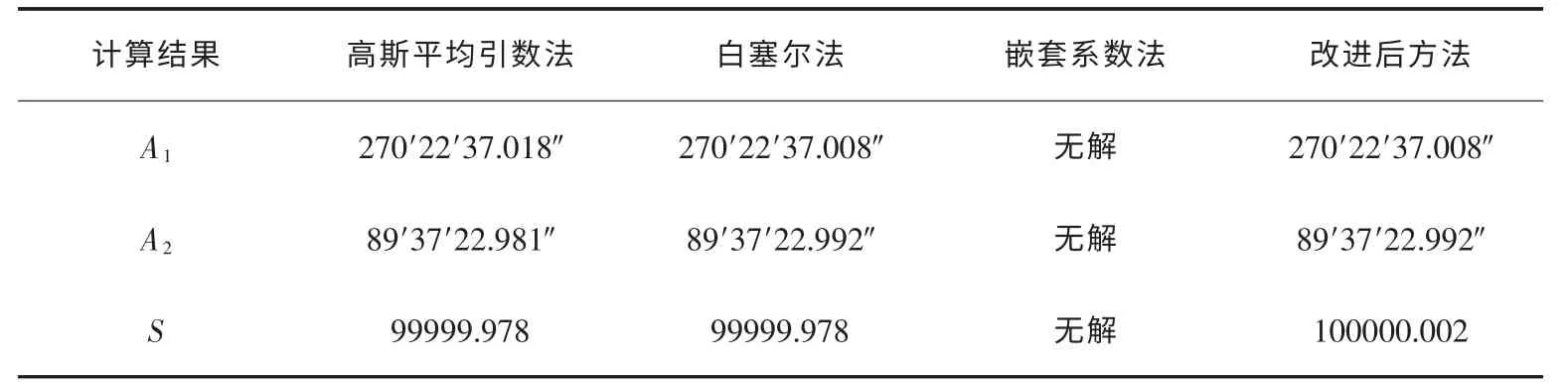
表1 例1 大地主题反解算例验证结果

表2 例2～例5 起算数据

表3 例2～例5 大地主题反解算例验证结果

以上所有例子都是大地线的起终点位于同一纬度时的情况，上面例子中大地线长度计算包括了从短距离到长距离， 以及大地线在赤道的情况，由于高斯平均引数法不适于计算大地线长度大于200 公里的主题解算问题，所以将例1 和其他例子分开验证，表2 中例5 采用的是文献[14]数据.

通过对上面例子数据的分析发现，当原嵌套系数法不能解算出大地线起终点在同一纬度的反解情况时，改进后方法能够解算出结果，和其他两种方法比较，结果满足要求. 因此改进后方法解决了原嵌套系数法反解中出现的问题，适用于任意距离的大地主题反解计算.

5 结束语

本文通过对嵌套系数法大地主题反解的研究，分析了嵌套系数法反解中当大地线起终点在同一纬度时出现的问题，并针对该问题提出了一种改进的算法，通过算例的证明，得出改进后的方法解决了该问题，结果是正确而且可靠的，同时对于大地线在赤道时的情况解算和判断更加简单. 嵌套系数法的改进使得有关大地主题方面的解算更加的完善，这将为洲际联测、导弹火箭和卫星发射等方面发挥重要的作用.

[1] 孔祥元，郭际明，刘宗泉. 大地测量学基础[M].武汉：武汉大学出版社，2010.

[2] 陈 健，晁定波.椭球大地测量学[M].北京：测绘出版社，1989.

[3] 徐晓晗，谢云开，李亚军. 大地主题解算实用算法[J]. 科学技术与工程，2012，12(9)：2062-2068.

[4] 周振宇，郭广礼，贾新果. 大地主题解算方法综述[J]. 测绘科学，2007，32(4):190-191.

[5] 周江华，苗育红，成文生，等. 贝塞尔大地反解问题的高效率算法[J]. 测绘学报，2002，31(2) : 108-111.

[6] 陈俊勇.长距离大地主题反算的直接解法[C]//国家测绘总局测绘研究所. 大地测量研究专辑：第一辑，北京：测绘出版社，1979 .

[7] 张志新.大地主题反解公式[C]// 国家测绘总局测绘研究所. 大地测量研究专辑：第二辑，北京：测绘出版社，1980.

[8] 史国友，周晓明，贾传荧. 贝塞尔大地主题正解的改进算法[J].大连海事大学学报，2008，34(1) : 15-19.

[9] 史国友，赵庆涛，王玉梅，等.贝赛尔大地主题反解的改进算法[J] . 交通运输工程学报，2009，9(1) : 77-82.

[10] 黄继文.按巴乌曼投影公式反解大地主题的新算法[J].解放军测绘学院学报，1994，11(2)：94-100.

[11] 范业明，王解先，刘慧芹.大地主题的数值解法[J].工程勘察，2007 (1) : 61-63

[12] 徐绍铨.弦线法解算大地测量主题精密公式[J].武汉测绘科技大学学报，1990，15(1)：19-27.

[13] 施一民，范业明.一种子午线正反解算的新方法[J].同济大学学报: 自然科学版，2005，33(7) : 964-966.

[14] 何 菊，胡 鹏，胡 海. 一种适用于任意距离的大地主题计算方法的研究和试验[J].测绘科学，2006，31(2)：29-31.

[15] 张学廉. 嵌套系数法--精密解算任何距离大地主题[J]. 武汉测绘学院学报，1985(1): 78-91.

[16] （美）索利斯（Solis，D.）.C# 图解教程[M]. 苏林，译. 北京：人民邮电出版社，2011.

[17] 黄建生，羊远新，王树东.大地主题解算电算化时应注意的问题[J]. 工程勘察，2006 (8):47-49.