新沂台地电场频谱特征的分析与研究

孙 雷， 李 飞， 杨冯威

(1. 连云港地震台， 江苏 连云港 222061 ； 2. 新沂地震台， 江苏 新沂 221400）

0 前言

地球表面的地电场是由地球外部的各种电流系在地球表面感应产生的， 分布于整个地表的广大地区， 这种天然的全球性或区域性的变化电场， 称为大地电场。 天然的稳定电场主要由矿体、 地下水和各种水系产生的， 分布于局部地区， 这种天然的地方性的稳定电场，称为自然电场。 以上二种电场总称为地电场[1]。

在我国， 小波变换理论在地球物理领域得到了广泛的应用[2～6]。 同时运用功率谱、 最大熵谱、 傅里叶变换等频谱方法对前兆资料进行频谱分析[7～10]也得到越来越多的运用。 随着计算机技术的快速发展， 小波分析与快速傅立叶变换越来越多的在前兆资料处理中得到了广泛的应用。 宋治平等[11]探讨了将小波变换理论应用于数字化前兆资料分析的可行性； 吴立辛等[12]运用小波分析对宁夏短水准资料进行了研究； 邱颖等[13]运用小波方法在地电场的干扰进行了分析研究； 顾申宜等[14]采用傅立叶变换和小波分解方法对海南水位仪的高采样率数字化水震波进行了频谱分析， 都说明数字信号处理技术在地震前兆数字处理领域具有很好的运用前景。

由于地电场观测过程中受到多种因素干扰， 为此张秀霞等[15]对新沂地电场的各类影响因素进行过相关研究， 新沂地电场的影响因素主要为： 雷电干扰、 降雨影响、 电阻率测量干扰、 场地固定干扰、 线路和仪器故障、 门限问题、 数据阶跃、 数据的长期飘移问题。 由于受到这些因素的影响， 在资料的选取过程中存在一定程度的局限性。

本文基于波动理论和振动理论， 剔除以上各类影响因素对新沂台地电场的干扰， 选取了新沂台不同月份地电场NS 与EW 向平稳变化时段的分钟值、 小时值数据， 结合地磁场H分量、 体应变数据， 运用快速傅里叶变换将各观测资料的优势周期分解而出， 进而运用小波分析分解为不同频率范围内的时间信号序列， 然后利用最小二乘法对分解后的信号进行求解， 以期得到各物理量之间的相互关系； 进而认识其产生的背景变化。

1 台站简介与资料基本情况

新沂地震台位于苏鲁交界的郯庐断裂带中南段， 东距黄海100 km 左右。 台站基岩主要是红色砂岩， 第四纪覆盖深浅不一。 在测区内， 其变化为东薄西厚， 变化范围在4～40 m 之间； 南北向覆盖层变化范围较小， 维持在4 m 左右。 观测仪器采用ZD9A－Ⅱ型地电场仪，测量频段为0～0.005 Hz， 资料产出为1 组/分钟。 共布NS 向、 EW 向和N45°E 向三个方向，每个方向又布长、 短二种极距， 其中NS 向、 EW 向长极距为400 m， 短极距为200 m；N45°E 向长极距为566 m， 短极距为283 m。 电极为Pb-PbCl2 不极化电极， 电极埋深为3.5 m， 外线路采用埋地方式， 观测系统的建设及布极区的环境状况均符合观测规范[16]。 连云港地震台位于新沂台正东约90 km， 其体应变资料连续可靠。

图1 2009年5月1日至31日新沂台地电场、地磁场H 分量、体应变曲线Fig.1 The curves of geoelectric field, geomagnetic vector H, volume strain in Xinyi station from May 1 to 31,2009

图1 为2009年5月1日至31日地电场NS 向和EW 向、 地磁场H 分量、 体应变小时值的曲线， 其中体应变因存在漂移现象， 故进行相关处理。 从曲线上可以看出： 地电场NS向和EW 向存在明显的潮汐波现象， 其中NS 向的日变化主要是呈现出双峰单谷的特点，EW 向排除资料存在干扰的天数外（如5月3、 14日）， 呈现出双峰双谷的特点。 地磁场H分量日变化形态为双峰单谷形态； 体应变的双峰双谷日变形态比较清晰。 图2 为2009-09-19～2009-10-17（阴历8月1日至30日）天文大潮前后的各测向小时值对比曲线， 地电场NS向的日变化主要是呈现出以双峰单谷为主， 但夹杂着双峰双谷的特点， EW 向主要呈现出双峰双谷的特点。 地磁场H 分量日变化形态为双峰单谷形态； 体应变的双峰双谷日变形态比较清晰。 图3 为2012年6月17日发生磁暴（k=6）前后各测向的分钟值对比曲线， 地电场NS 和EW 向的日变化受到电暴影响十分明显， 由于布极方式的问题， 两者呈现反向对应变化， 与地磁场H 分量对应性十分明显； 体应变没有受到电（磁）暴的任何影响， 呈现出清晰的双峰双谷日变形态。

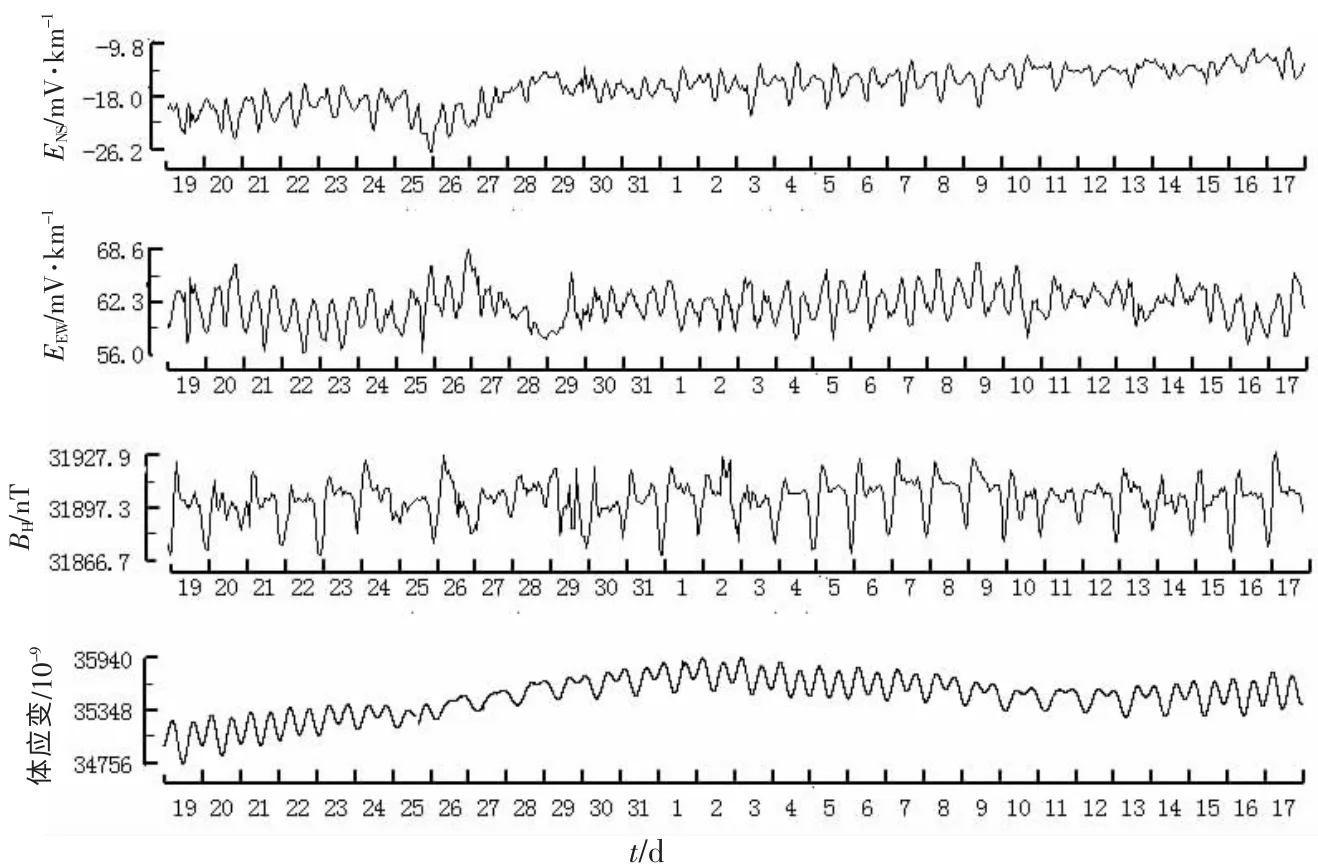
图2 2009-09-19～2009-10-17日新沂台地电场、地磁场H 分量、体应变曲线Fig.2 The curves of geoelectric field,geomagnetic vector H,volume strain in Xinyi station from Sep 19,2009 to Oct 17，2009

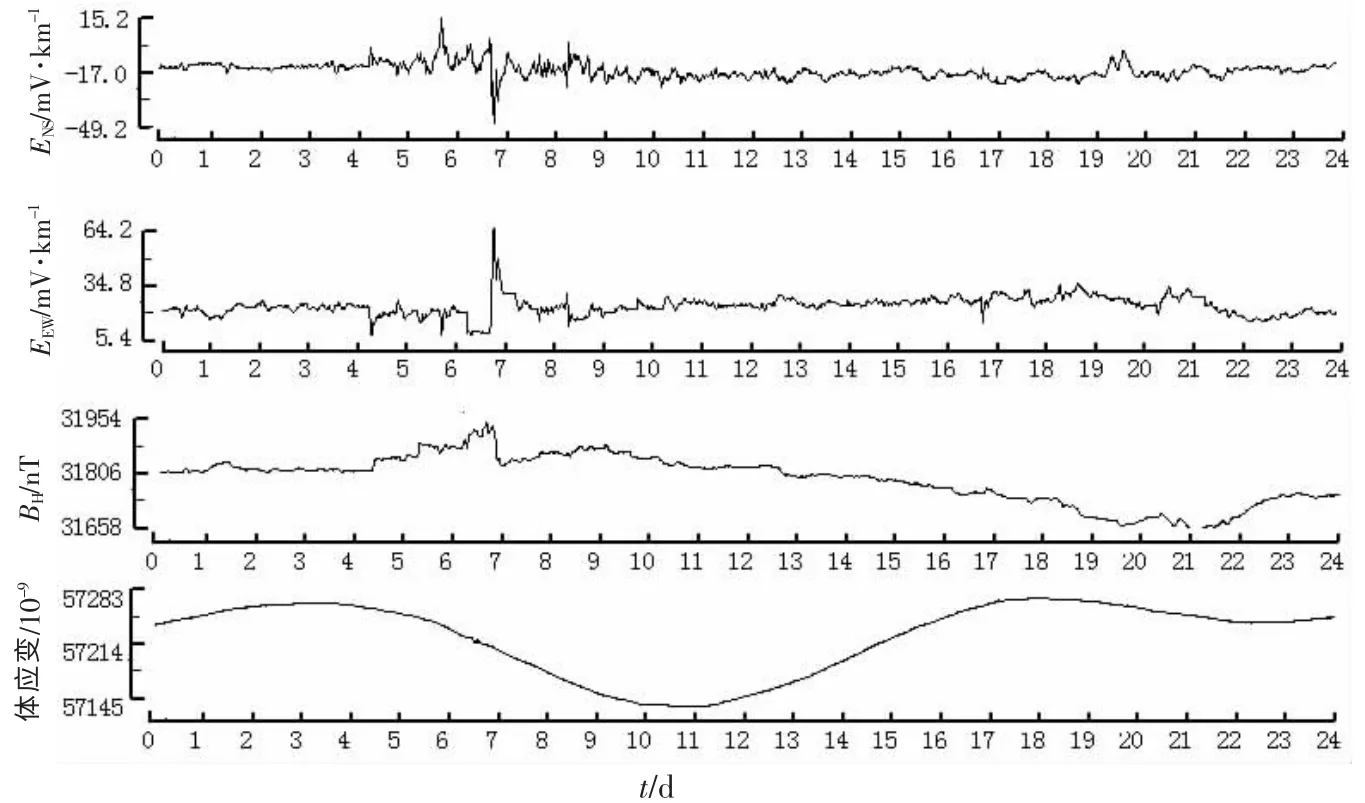
图3 2012年6月17日新沂台地电场、地磁场H 分量、体应变曲线Fig.3 The curves of geoelectric field, geomagnetic vector H, volume strain in Xinyi station on Jun 17, 2012

谭大诚等[17]将潮汐地电场分成近正弦TGF-A 型（双峰双谷型）和近梯形的TGF-B 型（双峰单谷型）， 并对其形成机理进行相关研究： TGF-A 型地电场与固体潮汐密切关联， 基本分布在大面积水域附近， 并与附近水域面积和距离、 岩性结构、 构造活动等因素有关； TGFB 型地电场与气潮作用产生的空间Sq 电流关系密切， 并与岩石饱和度、 渗透率等有关。 按照此理论新沂台地电场NS 向为TGF-B 型， EW 向为TGF-A 型。 与地磁场H 分量的日变形态相比， 地电场NS 向基本与其类似， 其峰谷变化十分对应； 地电场EW 向与地磁场H 分量对应性较差， 按照地电场EW 向布极方式， 其峰谷变化与地磁场H 分量应存在反向对应关系； 但2009年5月6、 25、 27日其谷值变化又存在类似关系。 与体应变的日变形态相比， 地电场NS 向峰谷变化与其对应性很差， 而地电场EW 向的峰谷变化与之对应性较强。对于新沂台地电场为何呈现出如此的日变形态， 以及与地磁场H 分量、 体应变的存在何种对应关系， 为此进行如下分析。

2 快速傅里叶变换分析

2.1 快速傅里叶变换原理

傅里叶变换的理论与方法在 “数理方程”、 “线性系统分析”、 “信号处理、 仿真” 等很多学科领域都有着广泛的应用， 采用傅里叶级数分解得到信号中含有哪种频率成分， 振幅多少； 由于计算机只能处理有限长度的离散的序列， 所以真正在计算机上运算的是一种离散傅里叶变换。 与直接计算相比， 用快速傅里叶变换算法可大大减少运算次数， 提高工作效率， 其滤波原理是对时间序列X(n)(长度为L)， 通过一个FIR 线性相位滤波器h(n)(节数为M， 长度为M+1)的计算过程。 其调用格式为：

式中x 是序列， 可以是一向量或矩阵， y 是序列x 的快速傅里叶变换的结果， 反应的是频率变化， 并且与x 具有相同的长度， N 为正整数。

利用基于MATLAB 的快速傅里叶变换[18]对地磁场H 分量、 地电场NS 向和EW 向、 体应变固体潮2009-05-23～2009-05-27、 2009-09-06～2009-09-10、 2010-01-06～2010-01-10的分钟值资料与2009-05-01～2009-05-31、 2011-01-01～2011-01-31、 2009-09-19～2009-10-17 小时值资料进行傅氏变换， 把时间域的数据变成频率域的幅频值； 通过对信号的频谱特征分析， 确定数据的周期构成； 选择适当的周期频段进行滤波， 经过傅氏逆变换得到滤波后曲线； 对各滤波曲线进行频谱对比分析； 总结不同曲线的频率构成与变化特征。 在资料的选取过程中， 首先选取各分量的平稳变化时段的资料， 同时尽可能排除各类干扰造成资料非正常变化的数据。

2.2 不同月份分钟值频谱分析

图4 为各物理量连续5 天分钟值频谱曲线。 对于地电场NS 向： 优势周期较为丰富， 6 h、 8 h、 12 h、 24 h 周期都存在， 且各月表现不同， 谱值也不同； 从1月到9月， 12 h 优势周期越来越明显， 谱值也逐渐增大。 对于地电场EW 向： 优势周期以12h 为主， 从1月到9月， 谱值逐月增大； 其它周期如8 h、 24 h， 由于12 h 周期过于明显， 不是十分显著。对于地磁场H 分量： 优势周期较为丰富， 8 h、 12 h、 24 h 周期都存在， 各月表现不同， 谱值也不同； 从1月到9月， 12 h、 24 h 优势周期越来越明显， 谱值也逐渐增大。 对于体应变： 优势周期为12 h、 24 h， 同样各月表现不同， 谱值也不同； 其它周期如6 h、 8 h、 24 h不是十分显著。 总体上， 各月的优势周期多少不尽相同， 表现为冬少夏多， 谱值大小变化也不同， 表现为冬低夏高。

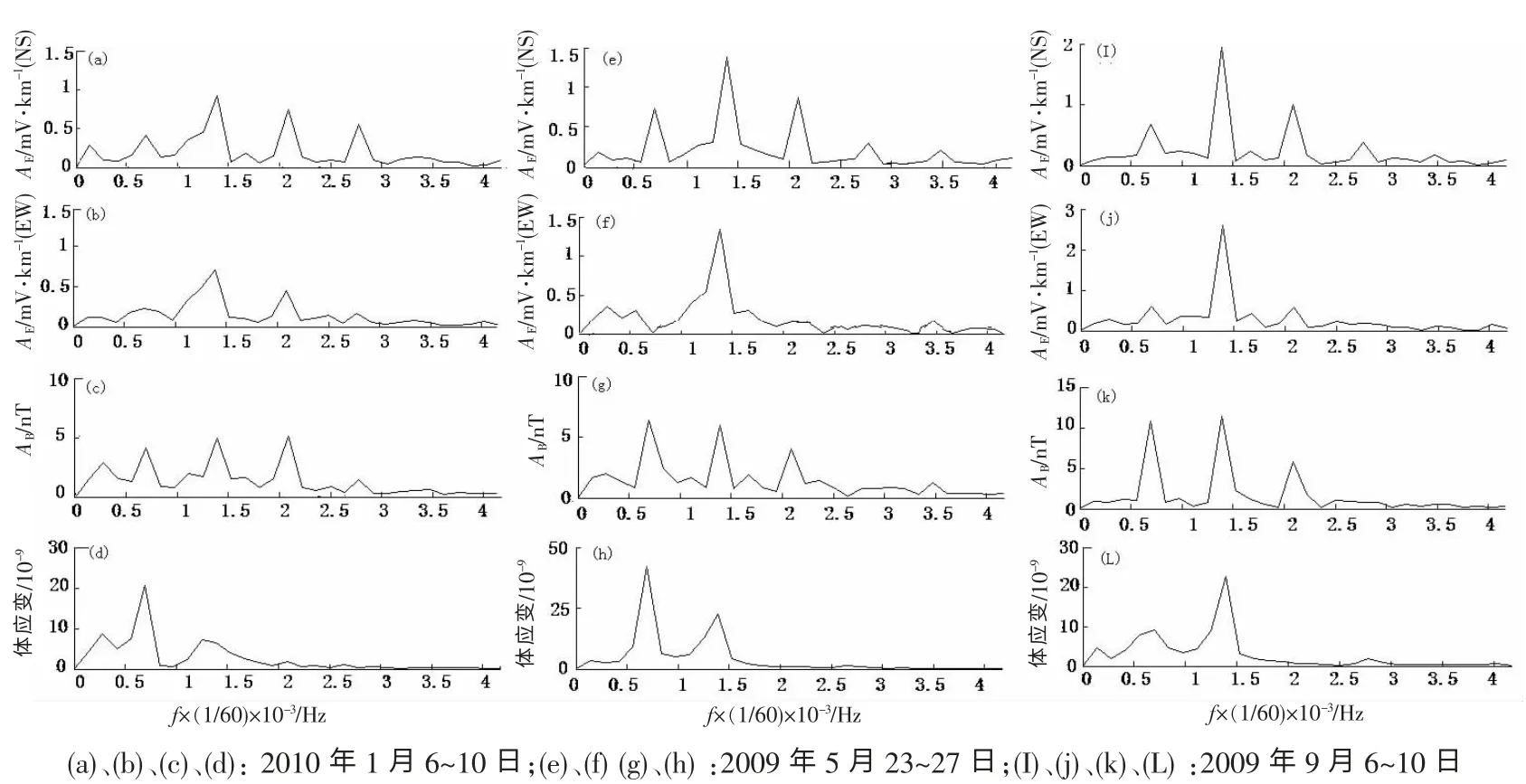
图4 新沂台地电场、地磁场H 分量、体应变频谱分析曲线Fig.4 The spectrum curves of geoelectric field, geomagnetic vector H, volume strain in Xinyi station.

从各分量优势周期的对应性来讲， 地电场NS 向同地磁场H 分量对应性最强， 与体应变的12h 优势周期有着一定的对应性； 而地电场EW 向的12h 优势周期及谱值大小的变化与地磁场H 分量、 体应变有着一定的对应性。 对于24h 优势周期， 地电场NS、 EW 向如同地磁场H 分量与体应变叠加的结果， 只是地电场NS 向含有地磁场H 分量的成分要高于体应变的成分； 而地电场EW 向更趋向于地磁场H 分量与体应变叠加抵充的结果， 这与地电场NS 向、 EW 向布极方式有关。 此外， 地电场EW 向的8h 优势周期与地磁场H 分量对应性较强（1、 9月份）。

2.3 不同月份小时值频谱分析

为了体现更长时间段的频谱对应性， 选取2009-05-01～2009-05-31、 2011-01-01～2011-01-31 以及2009-09-19～2009-10-17 天文大潮时的各物理量的小时值进行频谱分析，其结果如图5 所示。

从优势周期的对应性来讲， 地电场NS 向同地磁场H 分量对应性最强， 与体应变的12h优势周期有着一定的对应性。 而地电场EW 向的12h 优势周期与地磁场H 分量有着良好的对应性， 与体应变12h 周期对应性也很好。 对于体应变的24h 优势周期， 主要是由于其日变形态呈现出大、 小潮变化的结果。 而地电场EW 向呈现出类似正弦波的变化（见图1）。对于体应变出现的半月波周期， 地电场EW 向的对应性要高于地电场NS 向。 从谱值大小变化来看， 1月份较5月份、 9月份最大优势周期的谱值都低， 5月份、 9月份最大优势周期的谱值基本相当， 从而验证了季节变化是存在的。

对于天文大潮时的各物理量的频谱结果来看， 地电场NS 向的优势周期与1、 5月份的优势周期基本相同； 地电场EW 向的优势周期与1、 5月份的优势周期不尽相同， 12h 与半月波十分明显； 而体应变的优势周期与1、 5月份的优势周期基本类似， 只不过12h 周期较为突出； 地磁场H 分量的地电场NS 向的优势周期与1、 5月份的优势周期基本相同。

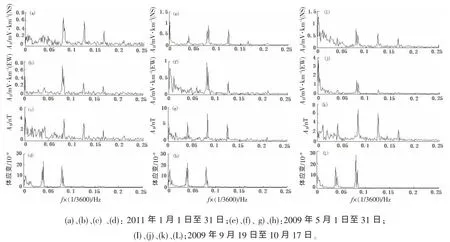
图5 新沂台地电场、地磁场H 分量、体应变频谱分析曲线Fig.5 The spectrum curves of geoelectric field, geomagnetic vector H, volume strain in Xinyi station.

通过以上分钟值频谱曲线、 小时值频谱曲线对比来看， 地电场NS 向与地磁场H 分量的各优势周期基本未发生变化， 只是最大优势周期略有不同： 地电场EW 向的12 h 优势周期都很明显， 体应变的12 h、 24 h 优势周期依然明显； 总体上地电场NS 向和EW 向的最大优势周期以12 h 为主， 地电场NS 向24 h、 8 h、 6 h 的优势周期较EW 向明显； 出现天文大潮时， 各物理量的优势周期变化不大， 对地电场EW 测向的影响相对而言偏大一点。此外， 不同年份、 不同月份各分量的优势周期不尽相同； 对于地电场12 h 以上的周期， 似地磁场H 分量与体应变叠加的效果， 其中地电场EW 向的对应性要高于地电场NS 向的对应性； 对于12 h 以下周期， 地电场NS 向与EW 向基本对应地磁场H 分量的周期， 其中地电场NS 向的对应性要高于地电场EW 向的对应性。

3 小波分析

由于傅里叶变换是将信号分解成正弦或余弦函数的叠加， 是从频率轴来分析该信号是由哪些频率的波组成的， 它只是将这些信息铺开到整个频率轴上。 而通过小波分析， 非稳定信号可以分解为小波的线性组合， 小波分析方法是一种时间窗和频率窗都可改变的时频局部化的分析方法， 即在低频部分具有较高的频率分辨率和较低的时间分辨率， 在高频部分具有较低的频率分辨率和较高的时间分辨率， 所以， 小波变换被称为数学的 “显微镜”。正是这种特性， 使小波变换具有对信号的自适应性。 小波分析优于傅立叶变换的地方是，它在时域和频域同时具有良好的局部化性质[19、20]。 为此运用小波分析对地电场、 电磁场H 分量、 体应变资料进行相关分析。

3.1 小波分析理论

其理论公式描述如下： 对于任意的一个函数f∈L2(R)，L2(R)为在R 上平方可积； 且基本小波ψ∈L2(R)，那么f 的连续小波变换可定义为：

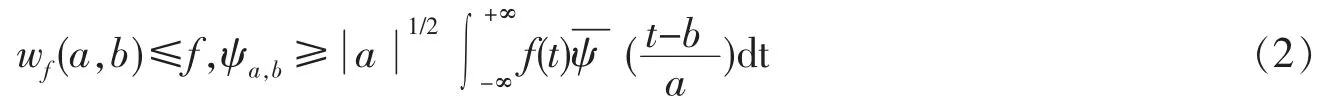
其中， α 为伸缩因子， 也称尺度因子， 它反映的是连续小波的尺度， 改变α 可使连续小波在横坐标上伸展或压缩， 即改变连续小波的形状； b 为平移因子， 改变b 可使连续小波在横坐标轴上移动。

3.2 数据分析

采用db4 小波对2009年5月小时值（图6a）、 2011年1月小时值（图6b）各物理量的数据进行6 阶分解。 根据以上FFT 频谱分析可知， 各物理量的优势周期基本在8h 以上， 由于1～2 阶的细节变化反映的是数据8h 周期以下的信息变化， 体现的是观测资料短周期的变化， 无法体现各物理量之间对应关系； 故利用3-4 阶的细节变化进行对比分析， 结果如图4 所示。 对于8～16h 周期的细节3： 无论是2009年5月还是2011年1月， 地电场EW 向与体应变的半月波非常明显， 其周期性变化对应性很强， 且相位差很小。 对于地电场NS 向与地磁场H 分量， 2009年5月两者的半月波比较明显， 但两者的相位差很大； 而2011年1月两者的半月波不太明显， 其中地磁场H 分量的半月波略微明显； 此外， 对于地电场NS向， 其波形变化如同是地磁场H 分量与体应变波形相互叠加的结果。

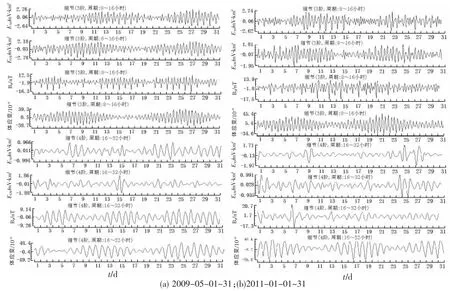
图6 新沂台地电场、地磁场H 分量、体应变小波分析曲线Fig.6 The wavelet analysis curves of geoelectric field, geomagnetic vector H, volume strain in Xinyi station

对于16～32h 周期的细节4： 地电场NS 向和EW 向与地磁场H 分量、 体应变的周期性变化对应关系明显低于细节3 的对应关系； 只是地电场NS 向的变化与地磁场H 分量相似度高些， 当然之间也似叠杂一定程度的体应变波形。 由此说明对于地电场16～32h 以上周期至半月周期的变化存在未明影响因素或关联因素。

4 各物理量日变幅对比分析

表1 为以上所选资料各物理量日变幅对比结果， 从中可以看出：

（1）地电场日变化呈现出明显季节变化： 1月与5月的日变幅偏低， 9月的日变幅偏高； 且5月的日变幅总体高于1月。

（2）1月与5月比较： 地电场NS 向的日变幅较EW 向高， 同时地磁场H 分量的日变幅总体同步， 体应变的日变幅的变化更加明显。

（3）在发生黄斑潮、 天文大潮前后， 虽然体应变的日变幅较其他时段没有突出变化，但在日变中， 其大小潮的变化十分弱化（见图2）； 而地电场EW 向的日变幅的变化量较其他时段都有明显的变化， 且日变幅也明显高于地电场NS 向的日变幅。 对于9月份地电场EW 向的日变幅比地电场NS 向的日变幅总体要高， 与天文大潮的来临有很大关系。

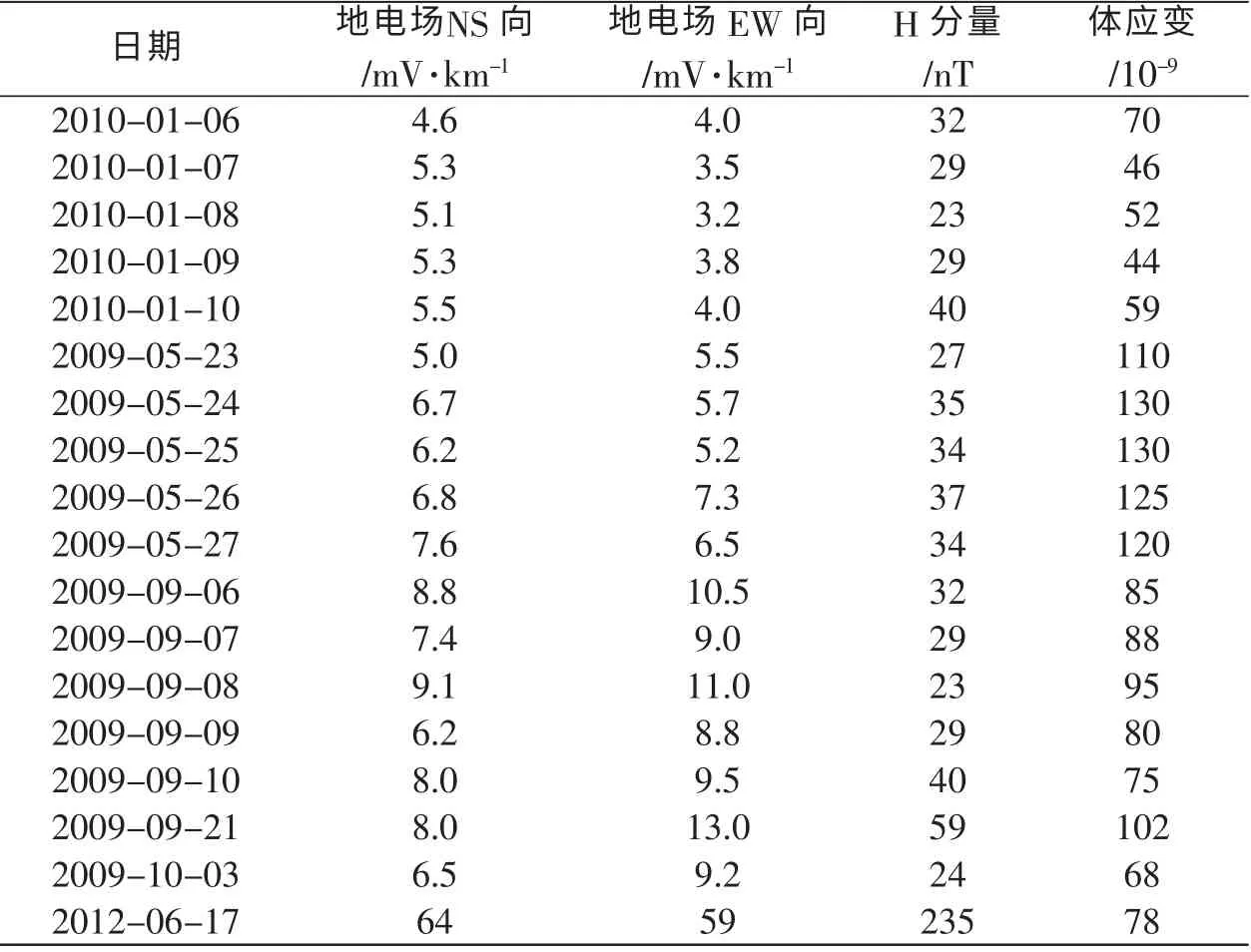
表1 各物理量日变幅对比结果Table 1 Comparison results of the daily variation amplitude of physical quantities

（4）在发生电（磁）暴时， 地电场无论NS 向还是EW 向，日变幅的变化与地磁场H 分量的日变幅的变化量都十分明显， 且地电场的两个测向的变化量的相差比例不大（与平稳时段相比）， 同期体应变的日变幅看不出特别的变化。

（5）无论哪个月份， 对于地磁场H 分量的日变幅的大小不同时而体应变的日变幅基本相同时， 地电场NS 向的日变幅与地磁场H 分量准同步对应。 同样， 对于体应变的日变幅的大小不同时， 而地磁场H 分量的日变幅基本相同时， 地电场EW 向的日变幅与地磁场H 分量准同步对应。 当地磁场H 分量与体应变的日变幅都大时， 地电场NS 与EW 向都同步变化。

5 讨论与分析

由于地电场与地磁场的快变化部分有相同的场源， 变化磁场最主要的平稳变化有太阳静日变化Sq 和太阴日变化L， 其变化周期分别是1个太阳日（24 h）和一个太阴日（24 h50 m）。 Sq 变化依赖地方时， 白天变化大， 夜间较平稳； 同时具有明显的逐日变化。 对于太阴日变化L， 具有半日波占优势和与月相有关两大特点。 因此平稳变化具有潮汐变化[18]。 大地电场谱成分中24～25 h 周期也是普遍存在的强周期成分， 这说 明24～25 h 的周期成分与大阳、 太阴周期活动有关。

根据孙正江等[21]研究， 北半球有8个电流涡旋场， 中低纬度的4个涡旋中心在30°附近， 这些涡旋电流场基本上按地理经度等间隔分布。 涡旋电流系的位置固定， 白天电流强、夜间电流弱。 地球自转一周， 各涡旋电流场的电流强、 弱交替一次， 白天两个强电流涡旋场、 夜间两个弱电流涡旋场引起地电场经历两次起伏， 所以产生大地电场的显著半日波周期成分。

对于地球产生的潮汐引力作用， 太阴活动引起的海潮、 固体潮已被精确记录到， 而地电场12 h 的优势周期成分正是日变化为2 峰2 谷波形的谱特征。 这种太阴活动引起的地球潮汐现象可能引起大地电场日变化。

太阳静日变化Sq 的幅度存在显著的季节变化， 都呈现出夏季变化大而冬季变幅小的特点[22]。 从而验证了地电场各分量的优势周期在不同季节不尽相同， 其幅值也呈现出夏高冬低的现象。 进而说明了地电场的变化和地磁场的变化密切相关。

通过表1 的2012年6月17日发生电（磁）暴（k=6）各物理量的日变幅变化可以看到， 地电场NS 向最大变化约64 mV/km， 地电场EW 向最大变化约59 mV/km。 由于发生电暴（磁暴）时， 引起地磁场与地电场的变化属于“同源”， 地电场NS 和EW 向都可以记录到与地磁场同步的明显影响。 说明这是地电场NS 向和EW 向表现出不同优势周期的一个原因。 而在200年发生天文大潮（阳历10月6日、农历8月18日前后）与黄斑潮（阳历9月21日、农历8月3日）时， 体应变基本看不出存在大、 小潮变化， 而地电场NS 和EW 向都呈现出双峰双谷的形态， 说明体应变的变化与地电场NS 向也存在一定的关联性。

由于地表结构对电场的影响对磁场影响要大[23]， 通过场地介绍可知， 新沂台地电场的场地存在各向异性： NS 向岩石埋深基本在4 m 左右， 而EW 向岩石埋深为4～40 m 左右； 即NS 向表层电阻率要高于EW 向表层电阻率。 从同场地的电阻率观测结果来看： NS 向电阻率维持在78 Ω.m 左右， EW 向电阻率维持在95 Ω.m 左右； 这是地电场NS 向和EW 向表现出不同优势周期的另一个原因。

在小波分析中， 8～16 h 周期的地电场EW 向和体应变， 其波形具有很高的一致性， 略有相位差； 而在16～32 h 周期的地电场EW 向和体应变， 可以说其波形完全对不上， 这是为何？ 由于新沂台地电场EW 向和和地磁场H 分量呈现反相位相关变化（与布极方式有关），在图6 中， 未将波形变化反向， 如果将图6 中4 阶的地磁场H 分量波形反向， 提取其Y 方向上变化， 再与体应变相叠加， 其变化形态与地电场EW 方向上的形态应有很大程度的吻合。 对于3 阶变化中， 地电场NS 向的波形变化， 也是不同分量相互叠加的结果。 其结果显示地电场各分量都可以记录到地磁场和固体潮变化， 只是叠加的量不同， 最终表现出较大的差异。

6 结论

（1）在稳定的背景场下， 通过对资料进行的FFT 频谱分析， EW 向优势周期只有12h的周期。 而NS 向就不尽相同： 其优势周期依次12h、 8h、 24h； 并且在不同年份、 不同季节其优势周期也不尽相同； 其总体变化遵从地磁场的变化。 通过小波变化分析， 地电场EW向具有较明显的半月波， 而地电场NS 向的半月波不如EW 向明显。

（2）同地磁场H 分量的优势周期相比， 新沂台地电场NS 向与其的同步性要高于地电场EW 向； 与体应变的固体潮的优势周期对比， 新沂台地电场EW 向与其的同步性要高于地电场NS 向。 尤其明显的是12h 以下周期两者基本遵从地磁场H 分量的周期， 说明其场源主要是地磁场； 其中， NS 向的变化更受地磁场的变化影响。 而太阴活动引起的海潮、 固体潮已被精确记录到， 说明固体潮的变化应是新沂台地电场产生变化的另一个场源， 从优势周期的对应性来看， 地电场EW 向的变化更受固体潮的变化影响。 地电场对于12h 以上周期， 似地磁场H 分量、 体应变的固体潮波形相互叠加、 抵消后造成的， 从而进一步说明了新沂台地电场是变化磁场和固体潮共同作用的结果。

（3）地电场优势周期的谱值也不尽相同， 总体呈现出夏高冬低的现象。 地电场的谱值大小与观测台台址的浅层电阻率有关， 电阻率越高， 大地电场各种周期成分谱值越大。

[1] 孙正江， 王华俊. 地电概论[M]. 北京： 地震出版社， 1984.

[2] 章珂， 刘贵忠. 二进小波变换方法的地震信号分时分频去噪处理[J]. 地球物理学报， 1996， 39 (2)： 265-271.

[3] 侯遵泽， 杨文采. 中国重力异常的小波变换与多尺度分析[J]. 地球物理学报， 1997， 40 (1)： 85-95.

[4] 杨文采， 施志群， 侯遵泽， 等. 离散小波变换与重力异常多重分解[J]. 地球物理学报， 2001， 44 (4)：534-541.

[5] 岳文正， 陶果. 小波变换在识别储层流体性质中的应用[J]. 地球物理学报， 2003， 46 (6)： 863-869.

[6] 楼海， 王椿镛. 川滇地区重力异常的小波分解与解释[J]. 地震学报， 2005， 27 (5)： 515-523.

[7] 叶青， 杜学彬， 周克昌， 等. 大地电场变化的频谱特征.地震学报[J]. 2007， 29 (4)： 382-390.

[8] 张燕， 吴云， 刘永启， 等. 小波分析在地壳形变资料处理中的应用[J]. 地震学报， 2004， 26 (增刊)：103-109.

[9] 朱涛. DEMETER 卫星观测的LF/MF 电场频谱特征初步研究[J]. 地震学报， 2010， 32 (4)： 476-489.

[10] 范莹莹， 杜学彬， Jacques Zlotnicki 等. 汶川MS8.0 大震前的电磁现象[J]. 地球物理学报， 2010， 53(12)： 2887-2898.

[11] 宋治平， 武安绪， 王梅， 等. 波变换在前兆观测资料中的应用[J]. 中国地震， 2004， 20 (1)： 31-38.

[12] 吴立辛， 卫定军， 李国斌， 等. 小波分析方法在宁夏短水准资料分析中的应用[J]. 地震研究， 2007， 30(1)： 49-53.

[13] 邱颖， 席继楼. 小波方法在地电场干扰处理中分析研究[J]. 地震， 2009， 29 (2)： 57-63.

[14] 顾申宜， 李志雄， 张慧. 海南地区5 口井水位对汶川地震的同震响应及其频谱分析 [J]. 地震研究，2010， 33 (1）： 35-42.

[15] 张秀霞， 李飞， 苏泽云， 等.新沂地震台新建地电场资料分析[J].华北地震科学， 2009， 27 (4)： 41-45.

[16] 中国地震局科技监测司. 地震地磁观测技术[M]. 北京： 地震出版社， 1995.

[17] 谭大诚， 赵家骝， 席继楼， 等. 潮汐地电场特征及机理研究[J]. 地球物理学报， 2010， 53 (3)： 544-555.

[18] 万永革. 数字信号处理的Matlab 实现[M]. 北京： 科学出版社， 2007.

[19] 高静怀， 汪文秉， 朱光明， 等. 地震资料处理中小波函数的选取研究[J]. 地球物理学报， 1996， 39 (3)：392-400.

[20] 蒋骏,李胜乐,张雁滨等.地震前兆信息处理与软件系统(EIS2000)[M]. 北京： 地震出版社， 2000.

[21] 孙正江， 王华俊. 地电概论[M]. 北京： 地震出版社， 1984.

[22] 徐文耀. 地球电磁现象物理学[M]. 合肥： 中国科技大学出版社。 2009.

[23] 中国地震局科技监测司. 地震及前兆数字观测技术规范（电场观测）[M]. 北京： 地震出版社， 2001.