船用厚板焊接温度场演变规律

殷苏民，江文林，王 匀，许桢英，张 超

(江苏大学机械工程学院，江苏 镇江 212013)

0 前言

随着焊接结构的大型化、复杂化和材料的高强度化，焊接难度越来越大。焊接时由于高度集中的瞬时热输入，焊后将产生相当大的焊接残余应力和焊接残余变形，引发热裂纹、冷裂纹、脆性断裂等工艺缺陷，在一定条件下将影响结构的承载能力，如强度、刚度和受压稳定性，以及结构的加工精度和尺寸稳定性[1-3]。提高和保证焊接质量已成为焊接关键问题。

通过数值分析技术可以预测焊接温度场和应力场的分布情况，从而指导工艺优化，获得高质量的焊接结构。但是焊接过程尤其是厚板焊接时，建立符合焊接热过程的热源模型是温度场和应力场分析的关键。通过热源模型可以获得符合相应焊接参数条件下的热流分布形式，使模拟的熔池边界线与试验观测的焊缝熔合线相符，进而得到与实际相吻合的温度场。

1 热源模型

相对于集中热源，平面分布热源和体积分布热源将能量依照一定规律分布于一定空间内，更贴近于生产实际。在焊接数值分析中常采用平面分布的高斯热源或体积分布的双椭球热源。当采用高斯面热源时，所模拟的焊缝熔宽大、熔深小，熔池呈浅碟形，无法准确反映焊缝内部熔池形状；当采用双椭球体热源时，由于考虑了熔滴过渡形成的内热源形式，所得熔池形状与实际焊缝熔合线较为吻合，但是熔池表面温度误差较大。由此将两者相结合得到组合热源模型，可以兼顾能量在熔池表面以及内部分布[4-5]。

1.1 正态高斯分布热源模型

研究表明，在电弧、高能束流和火焰焊接时，若熔深较浅，采用热流密度呈高斯正态分布的表面热源模型[6]，可分析焊接温度场。高斯面热源可以提高高温区的准确性，但仍未考虑电弧挺度对熔池的影响。高斯面热源的热流密度函数

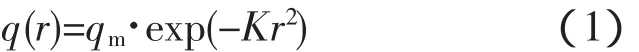
式中 q(r)为半径r处的表面热流密度；qm为热源中心的最大热流密度；K为热源集中系数，是与焊接方法相关的常数；r为距热源中心的距离。

1.2 双椭球形功率密度分布热源

对于高功率密度热源，比如激光与电子束焊，熔深较大，表面热源模型忽略了电弧和束流对表面以下熔池的挖掘作用，此时采用体热源模型分析温度场更为合适。以椭球形热源密度函数模型得到的焊接温度场也不能完全反映实际温度场的特征，热源中心前面的区域温度梯度较小，而热源中心后面的区域温度下降较快。实际的焊接温度场分布情形是在热源中心前面的区域温度梯度较大，而椭球的后半部分温度分布较缓。J.Goldak提出了双椭球功率密度分布热源模型[7]，该模型设定体热源的前半部分为1/4椭球，而后半部分为另1/4椭球。

设双半椭球体的半轴为(c1，c2，a，b)，设前半部分椭球能量分数为ff，后半部分椭球能量分数为fr且ff+fr=2，Q为热源总能量，则在前半部分椭球内热源分布为

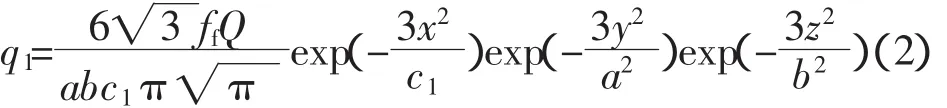
同样，对后半部分椭球内热源分布为

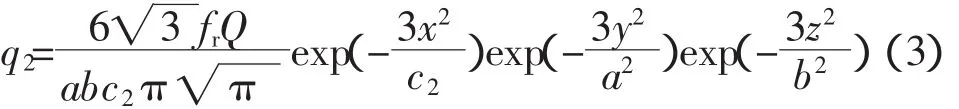
1.3 组合热源

采用单一面热源或体热源焊接热过程模拟时误差较大，研究发现结合面热源和体热源的组合热源模型所得的熔池形状与实际的焊缝熔合线基本吻合[8]。组合热源如图1所示，将总的输入功率按一定比例分配，此时总热流等于表面热流与体积热流两者之和。

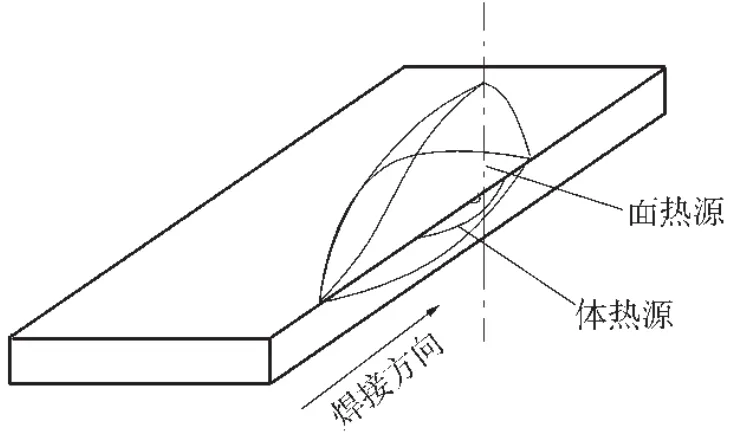
图1 组合热源模型

面热源与体热源的总功率与焊接的有效功率相等，即

式中 Φs、Φω分别为面热源和体热源的功率。将面热源功率所占总有效输入功率的比例系数称为功率分配系数，用γ来表示，则有

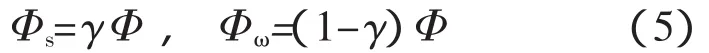
2 数值分析模型建立

焊接试样采用两块100 mm×100 mm×5 mm规格的钢板。总共分五个区域，中间区域用于模拟焊缝，与焊缝相邻的两个体用于模拟焊接热影响区，边上的两个区域用于模拟母材，如图2所示。

图2 分析区划分

焊接是一个高度非线性瞬态热过程，在接近焊缝区域温度梯度变化大，远离焊缝区域温度变化则较小。为保证精度和提高运算速度，采用不均匀网格划分法，在焊缝及其附近的部分采用加密的网格，在远离焊缝的区域，温度分布梯度变化相对较小，网格划分较粗。焊缝区网格大小0.5 mm×1 mm×1.25 mm，母材区网格大小 2 mm×8.5 mm×1.25 mm，本模型共18875个节点，14800个单元。ABAQUS热模拟选用DC3D8单元，划分结果如图3所示。

在实际焊接时，被焊工件将通过对流和辐射方式与外部环境（空气）进行热交换。在有限元计算时，焊接模型与周围空气之间的对流热交换可用Newton冷却方程描述为

图3 划分网格示意

式中 qa为工件与空气之间的热交换能量；ha为对流热交换系数；Ts为工件表面温度；Ta为周围空气的温度，取为20℃。假设ha是不随温度变化的定值，取值为10×10-6W/(mm2·℃)。

遵循Stefan-Boltzman定理，通过热辐射散失的热量可描述为

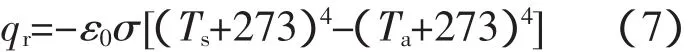
式中 ε0为辐射系数，取0.85；σ 为Stefan-Boltzman常量，取值 5.67×10-8W/(m2·k4)[9]。

3 对接焊接分析结果和讨论

采用间接耦合法进行厚板对接焊接数值分析。在同一模型上，通过Fortran分别施加高斯热源、双椭球热源及组合热源，其热流密度分布如图4所示。

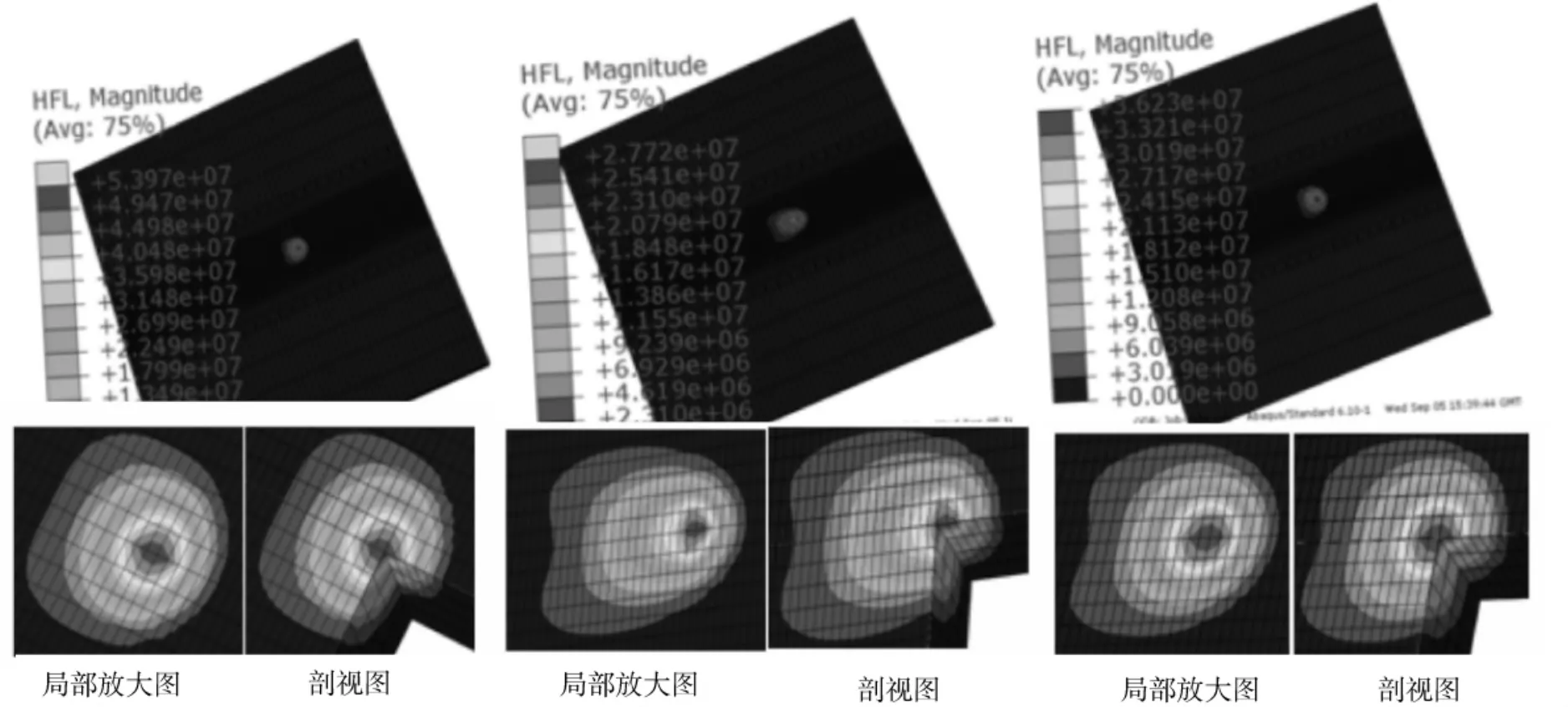
图4 不同热源下的热流密度分布（高斯热源，双椭球热源和组合热源）

图4显示在高斯热源模型下，热源近似成圆形且热流沿着厚度表层方向传递。在双椭球热源模型下，热源成椭球形状且热流沿着厚度方向传递。在组合热源模型下，热源在上表面近似成圆形，而在厚度方向近似成椭球且热流沿着厚度方向传递。

由图5可知，采用高斯面热源时的后方处切片温度传递较慢，所模拟的焊缝熔宽较大，熔深较小，熔池呈浅碟型，这是由固体金属的热传导方程决定的。采用双椭球体热源时的后方处切片温度传递的相对较快，熔宽较小，熔深较深，近似成柱形。在组合热源后方处切片熔池形貌开口较大，而内部逐步收敛成漏斗型，其熔池形状与实际的焊缝熔合线在金属内部较为吻合。

图5 焊接中期温度场热源后方处切片

焊接温度场前期、冷却中期、冷却结束时的温度场如图6所示，当选用高斯热源加载得到的温度场分布范围小，局部温度过高，表面最高温度达到3063℃，且只在表面加热，底部部分单元都没有被加热，仅仅通过热传导升温，面部的热源区温度场模拟较好，但温度在焊接过程中扩散不明显。当选用双椭球热源时，温度场分布范围大，最高温度偏低，最高温度为1969℃。虽然沿厚度方向的温度场比高斯热源更加贴近实际焊接，但温度场在焊缝表面分部的热源中心区没有高斯热源模拟效果好。组合热源的焊接温度场的分布范围和最高温度都介于高斯面热源和双椭球体热源之间，最高温度为2395℃，既考虑到电弧对母材的加热，又考虑到焊缝坡口形式对温度场的影响，符合电弧焊的传热特点，得到的温度场更符合实际情况。

图6 焊接温度场前期、焊接温度场冷却中期、焊接温度场冷却结束

图7 为 A（0，0.05，0.005），B（0.003，0.05，0.005），C(0.006，0.05，0.005)，D(0.016，0.05，0.005)，E(0.0245，0.05，0.005)五点的热循环图。如图7所示焊接过程中各点的温度变化十分不均匀，焊缝区温度变化比较快，而远离焊缝区各点温度变化比较慢。从热循环曲线分布图可以看出，在焊缝中心处，当焊接热源移动到A点时，焊缝中心的温度急剧上升到约3063℃，距离焊缝中心3 mm处的B点达到峰值温度约700℃，而距离焊缝中心最远的E点达到峰值温度约70℃。由于热传导作用，距离焊缝中心越远的最高温度越低，变化趋势也相应平缓。各点温度的变化规律基本一样，各点到最后时刻温度都是趋近一致，焊件上每个点温度由低而高，达到最高值后，又随时间逐渐变小。各点的升温速度明显比冷却速度要大；冷却时，各点温度逐渐趋于某一值，也就是整个焊接试件的温度趋于均匀。

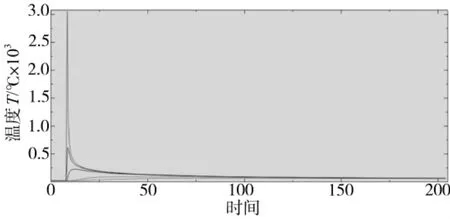
图7 热循环

4 结论

（1）建立了以厚板对接焊接的数学模型和物理模型，进行焊接过程温度场三维数值分析研究，跟踪整个焊接过程中焊接温度场的发生、发展和分布规律，以及各个节点的热循环曲线变化规律，理论结果与实际一致。

（2）对比了面部加载高斯热源、双椭球热源和组合热源模型，以及各热源模型在数值分析中的温度场分布情况，研究发现采用组合热源的熔池形状与实际的焊缝熔合线吻合性较好。结果表明，组合热源分析最为准确，为减小和控制焊接应力和变形提供依据。

[1]田锡唐.焊接结构[M].北京：机械工业出版社，1981.

[2]拉达伊，熊第京.焊接热效应温度场、残余应力、变形[M].北京：机械工业出版社，1997.

[3]陈 楚，汪建华，杨洪庆.非线性焊接热传导的有限元分析和计算[J].焊接学报，1983（3）:139-148.

[4]鹿安理，史清宇，赵海燕，等.厚板焊接过程温度场、应力场的三维有限元数值模拟[J].中国机械工程，2001，12（2）：183-186.

[5]武传松.焊接热过程与熔池形态[M].北京：机械工业出版，2007.

[6]Cao Z，Dong P，Brust F W.A fast thermal solution procedure for analyzing 3D multrpass welded structure[J].WRCBulletin，2000，4(55)：12-21.

[7]Wu CS.Computersimulated of three-dimensional convection in traveling MIG weld pools[J].Engineering Computation，1992，9(5)：529-537.

[8]盖登宇，褚元召.组合热源模型在焊接数值模拟中的应用[J].焊接学报，2009，21141:33-38.

[9]刘 敏，陈士煊，康继东.钛合金平板电子束焊接残余应力数值分析[J].航空力报，2001，16(1)：63-66.