运用纵横二维框架比较中新教科书中“勾股定理”

章健楠，叶立军

目前，新加坡已经逐步形成稳定的、具有自身特色的数学课程体系，[1]对于同处于东亚地区、与其文化背景极为相似的中国来说，比较、研究中新两国数学教材，有利于取长补短，同时也能够为数学教育打开新思路。本文选用Charalambos Y.Charalambous等在文[2]中建立的纵横二维研究框架，对人民教育出版社的《数学》（以下简称人教版教材），[3]以及新加坡Multimedia Communications Press出版社出版的New Express Mathematics（以下简称NEM教材）[4]中的“勾股定理”进行比较研究。

一、研究背景

（一）选取“勾股定理”的理由

勾股定理作为几何学中的一颗明珠，是整个平面几何的基础，在现实生活中也被广泛应用。在教材编排中，勾股定理被安排在初中八年级教材中。此时正值学生由具体思维向形式化思维转变的时期。而在“勾股定理”这一章中，学生通过学习勾股定理及其逆定理的发现、证明与应用等内容，将接触到数形结合、转化等多种数学思想方法，为之后形成良好的形式化思维打下基础。

（二）所选取的研究重点

在本文所比较的两本教材中，都淡化了勾股定理的证明过程。两本教材中关于“勾股定理的应用”部分的内容均占据了相当大的比重，NEM教材更是将“运用两个定理解决实际问题”单独列为一个小节的内容。因此本文将研究重点放在了本章中的应用部分（即习题、范例）上，而非对每个知识点及证明方法的具体分析。

（三）所研究的问题

根据所选取的研究重点，本文将运用纵横二维研究框架建立编码系统，通过分析、比较习题、范例、知识点编排顺序等内容，来研究两本教材对于“勾股定理”这一章节的内容呈现方式上有何异同点，以及教材对学生的期望分别是什么。此外，基于问题的所得出的结论，作者还将对两国教材的编写做一些思考。

二、研究框架及编码

（一）研究框架

Charalambos Y.Charalambous等将目前国际上常用的两种教材分析方法---横向比较与纵向比较结合在一起，建立起一种新的二维研究框架。在这一结构中，横向包括背景信息和整体结构2个部分，纵向包括与学生交流、对学生的要求、联系3个部分。[5]

（二）编码系统

1.横向维度（见表格 1）

表1

2.纵向维度（见表格 2）

表2

纵向维度建模思维·数形结合思想·转化思想·方程思想对学生的要求认知要求·记忆型(任务需要对之前学过的知识，如等边三角形性质、等腰三角形性质、三角形的面积计算公式作简单回忆，不需要理解)·有联系型程序（任务集中在选择解决问题的程序上，与概念理解相关）·做数学（任务并未暗示可以预期的解题途径，需要将具体现象上升为本质联系，进行复杂的思考，设计方案解决问题。如勾股定理在实际生活中的应用）作答类型·只要求一个答案（数值或数值表达式）·答案或数学陈述·推理论证

（三）指标的度量

1.横向维度指标的度量

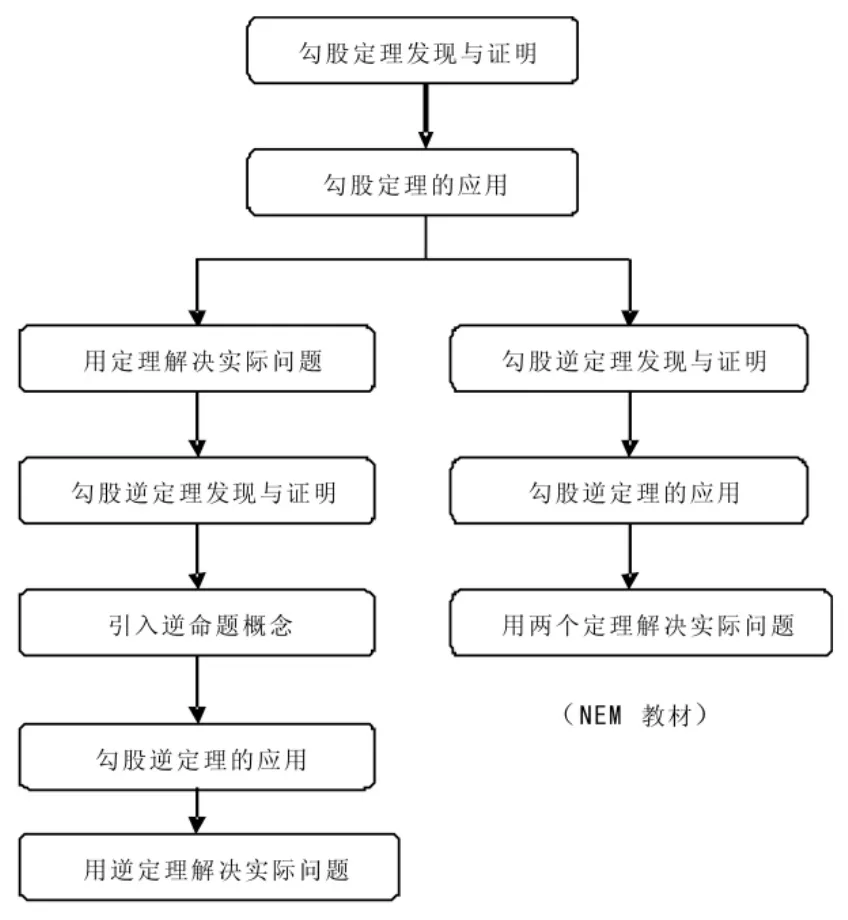
图1 主要内容与顺序统计

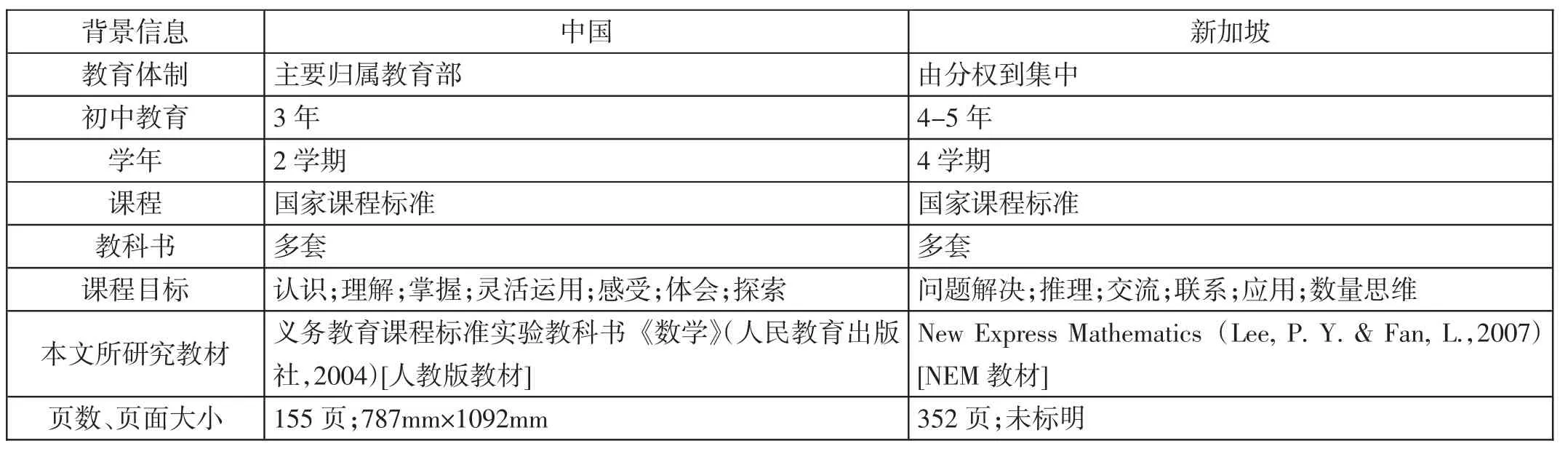
表3 背景信息统计

2.纵向维度指标的度量

说明：对于纵向维度中的其余各部分的统计结果，将在下文“研究结果”部分直接给出，此处不再以表格形式呈现。

三、研究结果

（一）教材呈现方式

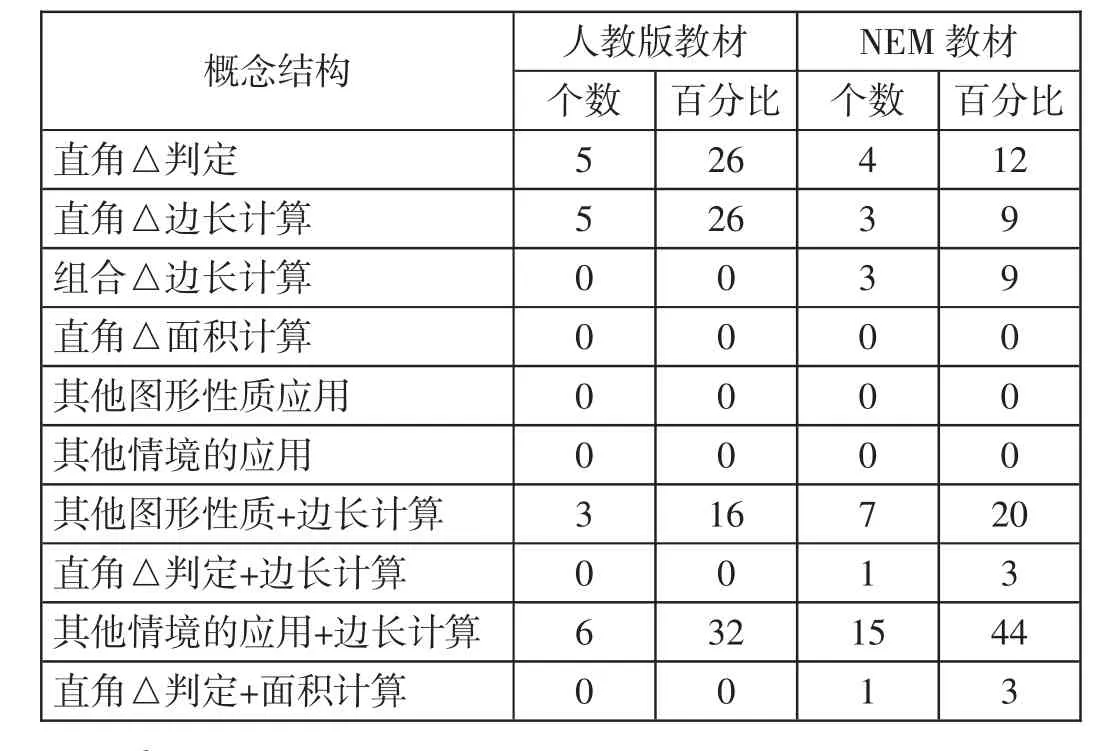
表4 不同概念结构（针对任务）统计

通过比较教材主要内容与顺序（见图表1），能够发现两本教材在内容选择上基本一致，但是在顺序编排上有所差异。人教版教材在证明了勾股定理之后，所设置的课后习题大部分为实际应用问题，解题难度较大。而在NEM教材中，7.2小节“勾股定理”与7.3小节“勾股逆定理”的课后习题都是简单、直观的边长计算。“用勾股定理解决实际问题”被单独列为本章的最后一个小节。作者认为NEM教材的编排顺序更为合理。

（二）教材对学生的期望

在NEM教材中，涉及数形结合思想、方程思想、转化思想等数学思想的任务占总数的百分比为82%，人教版教材为68%。如此高的比例可见培养学生数学思维在初中阶段越来越被重视。从认知要求的角度来看，两本教材都属于高认知要求。教材中的低水平任务（即记忆型任务）所占的百分比较低（NEM教材15%，人教版教材11%）。两本教材中都只有21%的任务只要求学生给出一个答案，其余都需要进行数学陈述。另外，人教版教材还引入了“逆命题”这一概念，并在任务中包含了部分需要推理论证的题目，对学生提出了更高的要求。基于以上比较结果，作者认为人教版教材对学生的期望要略高于NEM教材。

四、启示

（一）“高期望”是否等于“高质量”

在上面文中作者得出了“人教版教材对学生的期望更高”的结论，但事实上在教学评估中新加坡的教学质量总是高于中国，可见教材对学生的要求高并不一定能使得学生的知识水平高。中国学生的自主探究能力还不能达到教材要求的水平，这使得更多的时候需要教师去引导学生完成探究，学生的主体性反而减弱。

（二）教材所传递的新理念

两本教材都淡化了勾股定理的证明，增加了实际应用问题的数量。这一特点向我们传达一个讯息：如何将所学知识更好地运用于生活，提高学生的实际应用能力在数学教学中越来越受到关注。另外，NEM教材在本章节中多次使用了图形软件来进行教学。将信息技术与数学课程进行整合可以说是数学教育发展的必然趋势，但是在中国的教科书中还不常见。

（三）对所用研究框架的评价

Charalambos Y.Charalambous等在建立研究框架时设置了纵横两个维度，很好地弥补了之前单一维度框架的缺陷，既能研究教材细节又能从总体上把握教材内容，并能够研究不同教材对学生的不同期望，在教材比较中值得被借鉴。但也存在一些缺陷，如在纵向维度中所包括的“学生的态度”、“教材与课堂之间的联系”等指标。因此，作者认为该研究框架的纵向维度上可以再设计一些理论性的指标。

[1]张维忠,李芳奇.新加坡与中国数学教材的特色比较[J].外国中小学教育,2009，(02):32-36

[2]Charalambos Y.Charalambous,Sean Delaney,Hui-Yu Hsu and Vilma Mesa.A Comparative Analysis of the Addition and Subtraction of Fractions in Textbooks from Three Countries[J].Mathematical Thinking and Learning,2010,(12):117-151

[3]义务教育课程标准实验教科书[M].北京：人民教育出版社，2008

[4]Lee,P.Y.&Fan,L.(Eds.)New Express Mathematics.Singapore,Multimedia Communications Press,2007

[5][6]袁思情，陈月兰.一篇值得推荐的数学教材分析框架文章[J].数学教学，2011，（04）：21-24