基于动态参数模型的行人流疏散仿真

李特朗,张 喜,朱 诺,曹 伟,郑 攀

(1.北京交通大学交通运输学院,北京100044;2.中国民航科学技术研究院,北京100028; 3.国家烟草专卖局,北京100045)

基于动态参数模型的行人流疏散仿真

李特朗1,3,张 喜*1,朱 诺2,曹 伟1,郑 攀2

(1.北京交通大学交通运输学院,北京100044;2.中国民航科学技术研究院,北京100028; 3.国家烟草专卖局,北京100045)

本文基于元胞自动机理论建立了行人疏散动态参数模型.其中,动态参数分别为∶空格参数、感知参数和方向参数.该模型模拟了行人决策过程和策略,反映了行人对周围环境的判断及行人的决策行为.根据摩尔近邻的二维元胞自动机,构造了行人移动规则并对行人疏散进行模拟.为显示本模型的优越性,在相同情况下,对原模型和本模型的模拟实验结果进行比较和分析.本文所建模型中,考虑了出口周围的行人密度对疏散过程的影响,通过模拟结果证明,这种改进是有效的.同时,本文也考虑了行人分布、行人密度以及出口宽度对疏散时间的影响,并给出了疏散空间最优出口布局.因此,所建模型对于行人疏散研究和实际生活中有效避免和减少人员伤亡具有一定意义.

交通工程;行人疏散;元胞自动机;空格参数;感知参数;方向参数;疏散时间

1 引 言

公共场合中的人群聚集通常是事故发生的隐患,人群聚集拥挤度越高,事故风险越大,而且造成的人员伤亡和损失也更为严重.近几年,有很多专家和学者已经把研究重点放在公共场所的行人疏散仿真方面,并从物理角度出发,取得了很多喜人的成果.Yang等[1]提出了模拟疏散过程人群亲缘行为的二维CA模型.Yuan等[2]提出了解决多出口条件下人群疏散问题的二维CA模型.Varas等[3]通过考虑是否存在障碍物,建立了二维的CA模型,解决了存在障碍物时行人疏散仿真问题.Yu等[4]在描述环境对行人影响的同时,引入交感半径参数,建立了不后退的二维CA模型.Weng等[5]建立了模拟行人异步速移动的不后退CA模型,实现了行人的动力学仿真.Song等[6]提出了单出口条件下疏散仿真模型CAFE,并提出了摩擦力、斥力和引力是紧急疏散情况下引发人群复杂行为的基本源力.Kirchnera等[7]为仿真竞争外出行为,在二维CA模型中引入摩擦力概念.Nishinari等[8]通过对比蚂蚁与疏散者模型,研究了蚂蚁与人员疏散轨迹的相似性.Yue等[9]通过动态参数对行人疏散流进行模拟仿真,考虑了8种出口布局条件下,安全出口布局的不平衡对行人疏散过程和疏散时间产生的影响.但模型中主要考虑了方向参数和空格参数,并没有考虑拥堵状态下对行人疏散策略的影响,与此同时,Yue等[9]只是主观设置出口位置和宽度,并没有考虑最佳出口布局,本文所建模型是在这两个参数的基础上,引入感知参数,动态分析不同出口的拥挤程度对疏散路径和疏散时间的影响;通过模型模拟,给出了最佳的出口位置以及出口宽度,这对行人疏散及建筑工程方面都有一定的指导意义.

2 问题描述与建模

行人平均疏散时间定义为系统内所有疏散行人离开房间时所需要的时间步.模型建立在一个大小为(W+2)·(W+2)的二维离散元胞网格系统内,用离散元胞表示被分割的疏散空间,共W·W(W表示系统规模)个,房间围墙由系统边界的障碍物元胞构成,安全出口用围墙的空格元胞构成.系统内的每个元胞空格和行人是一一对等的关系.用等时间步长离散化行人仿真,行人可以在各个时间步长内选择向周围移动或等待.定义行人数量N与系统内元胞数量的比值为行人流密度K;定义行人疏散完毕时的时间步为平均疏散时间T.

2.1 动态参数计算

(1)方向参数.

行人疏散不是没有目的和方向地移动,安全出口位置是其移动的目的地,安全出口方向是其移动的方向,故行人会将下一时间步目标定在离安全出口近的位置.从方向参数角度,在移动领域内行人选择的位置与安全出口的距离接近程度即为时间步长内行人移动一个步伐获得的移动收益.计算方向参数时,不同位置对行人的吸引程度用静态领域表示.基于欧式距离的静态领域参数值可以按照下式表示:

式中 Sxy为元胞(x,y)静态领域参数值;(x,y)为元胞在疏散房间中的坐标;(xmn,ymn)为第m个门内第n个元胞在疏散房间中的坐标;M为一个很大的正数,说明障碍物对行人几乎没有吸引力.

因此,通过静态领域参数值,我们定义方向参数矩阵为

式中 S00为移动领域中心位置的静态领域参数值;Sij为行人移动领域内的静态领域参数值.

该式表明:在疏散行人占据中心位置的移动领域内,当方向参数值为0时,说明疏散行人在下一时间步长内选择该位置时,行人不会远离也不会接近安全出口;方向参数值大于零时,行人选择的位置时接近安全出口;当方向参数值小于零时,行人选择的位置则远离安全出口.

(2)空格参数.

空格参数反映下一步可选位置是否被其他行人占据:

(3)感知参数.

众所周知,行人是个智能体,会对周围的动态环境有感知效应.对于某个行人而言,在选择下一步移动的位置的时候,除了要考虑最短距离以外,而且要考虑周围环境的影响.比如出口宽度和行人的拥挤程度:一般情况下,某个出口的密度越小,对行人的吸引力就越大;某个出口的宽度越大,对行人的吸引力也就越大.在本文中,假定行人对周围环境熟知,并能根据实时的动态信息选择最短的疏散路径,这就需要行人对最短疏散路径和出口密度进行耦合和感知,保证行人以最短的时间离开疏散空间.因此,本文引进了感知参数,主要是考虑出口附近的行人密度及出口宽度对疏散时间和疏散路径的影响(假设在疏散的过程中,行人同时顾及两个因素,权重相等且分子与分母相互抵消).因此,我们定义感知参数矩阵如下:

式中 dm为第m个门的宽度;dL为门的总宽度;为t时刻疏散空间内行人的数量;为t时刻第m个门附近的行人数量;为t时刻疏散空间的面积;为t时刻第m个门的疏散面积.

图1 第m个门的疏散面积Fig.1 The count-area for exit m

2.2 演化规则

(1)疏散行人在单一时间步长内只移动一个元胞长度.行人下一步目标位置可以选择向周边位置移动或在原地等待,共有9个备选位置(如图2(a)).

(2)9个备选位置都各自拥有动态参数和移动收益(如图2(b)),其中,感知参数、方向参数和空格参数总和构成移动收益.kD、kE、kC分别为与方向参数、空格参数、感知参数相对应的权重系数,且kD+kE+kC=1.其中kE≥kD+kC,这是因为模型中假设一个元胞只能存在一个行人,如果一旦目标元胞被其他行人占据,即使方向参数和感知参数所获的收益很大,那么行人也不会进入该元胞.在每个时间步内,行人会根据其移动领域内每个位置的移动收益来判断下一步的运动方向和目标元胞.

Pij=kD·Dij+kE·Eij+kC·Cij(5)

图2 疏散行人移动领域及其相应的移动收益矩阵Fig.2 The movement rield and associated matrix of transition payoffs for evacuation pedestrian

(3)疏散行人首先判断和计算9个被选位置的移动收益,将下一步的目标位置确定为其中拥有最大收益值的位置.

(4)当拥有移动效益最大值的元胞位置存在多个时,下一步目标位置为行人以相同的概率在其中随机选取的元胞.

(5)当存在一个空闲位置被多个行人竞争的情况时,以相等概率被系统随机选择一个行人会占据该位置,并在下一步内移到目标位置.

(6)疏散行人移至门内时,行人将在下一时间步长内移出系统,此时行人将移出房间.

(7)当所有行人都移出系统后,即房间内行人移出完毕,仿真过程结束.

3 模拟分析

疏散行人在仿真的初始时刻均匀地分布于系统房间内.为了显示本文所建模型的优越性,我们与原模型[9]进行了比较分析(如图3).通过图3我们可以看到当密度K＜0.3时,原模型与本文所建模型的差别较小,这是因为此时密度较小,基本上所有的行人都可以轻松地到达自己的目的地,各个门前的密度差别不大,所以感知参数影响较小;而随着密度的不断增大,当K≥0.3时,行人之间的相互作用逐渐增多,有时不能按照自己的意愿到达目标元胞,从而产生了拥堵,而此时,行人在选择疏散路径时,往往倾向于选择密度较小的出口,从而减少疏散时间.随着行人密度K不断增加,这种现象就越加明显,因此两个模型之间的疏散时间差距越来越大.

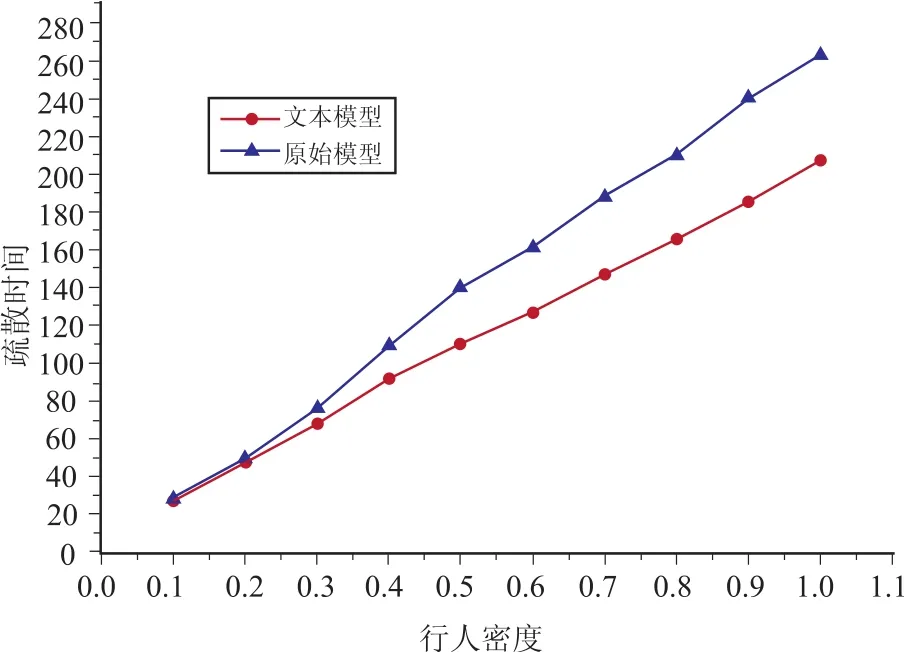
图3 改进模型与原模型的比较,W=20,L=1Fig.3 Comparison with the original model,W=20,L=1

为了寻找最佳出口布局,我们以系统规模W= 20为例,对周围墙的元胞进行了数字标定,作为门的可选位置,实际情况也同时被考虑进来(各个顶角不设置门,如图4(a)),图4(b)显示,随着数字值的增大,疏散时间呈双“W”型波动,最小的疏散时间往往出现在墙的中心位置,以W=20为例,最小疏散时间出现在10,30,50,70.通过对不同系统规模的模拟,我们也发现了同样的现象.通过理论推导,我们可知,疏散时间的大小往往依赖于行人所在的位置与出口之间的距离,当行人数量和位置固定时,求解行人的疏散时间往往等价于求解行人总的疏散距离,而最小的疏散距离是所有行人疏散距离的算术平均值,而根据计算可知,这个值往往接近于墙的中心.因此,我们建立模拟系统,即四个安全出口分别设置在墙的中心,进而寻找出口的最佳宽度.

图4 出口的最优位置,其中W=20,L=1,K=0.3 Fig.4 The optimal exits position

图5描述了当系统规模确定的情况下(W= 20),出口宽度、行人密度与疏散时间的相互关系.为了更加直观地显示其相互关系,我们进行了曲线的拟合(如图6).选取了当出口宽度为1时,拟合行人密度与疏散时间的变化曲线,我们发现其满足线性关系,当出口宽度大于1时,线性关系不变;与此同时,选取了行人密度为1时,拟合出口宽度与疏散时间的变化曲线,发现其满足负指数关系,当密度小于1时,变化曲线类似.因此我们得到结论,随着密度的增加,行人的疏散时间呈线性增长;随着出口宽度的增加,行人的疏散时间呈非线性增长(服从负指数分布).这与原模型得到的结论相同,但却有不同的物理意义.原模型只考虑了最短距离情况下的行人疏散,即无论该出口拥堵情况如何,行人不会改变疏散策略,始终把该安全出口作为自己的最终目标;而本文所建的模型,在最短距离的基础上,考虑出口密度的影响,即行人会根据出口附近的拥堵情况,改变自己的疏散路径,选择密度较小的出口作为自己的目标,尽量地减少排队现象,从而减少疏散时间.从图5我们发现,随着出口宽度的增加,疏散时间逐渐减少,但是到达一定宽度以后,疏散时间并没有明显的变化,这是因为此时出口利用率已经达到最大,疏散时间不会再有太多的改进.而在不同密度下,这个饱和值是不同的,比如当密度K=0.1时,饱和值为L=3;当密度K=1时,饱和值为L=5.为了确保行人的安全疏散并且不浪费资源,我们建议此模拟系统最佳的出口宽度为5.同理,我们可以找到其他疏散系统最佳出口位置和最优宽度.

图5 出口宽度、行人密度与疏散时间的相互关系,其中W=20Fig.5 The evacuation time versus exit width and pedestrian density when W=20

根据出口的最佳位置和最优宽度,我们对该模拟系统的疏散过程进行了仿真(如图7),其中W= 20,L=5,K=0.5.

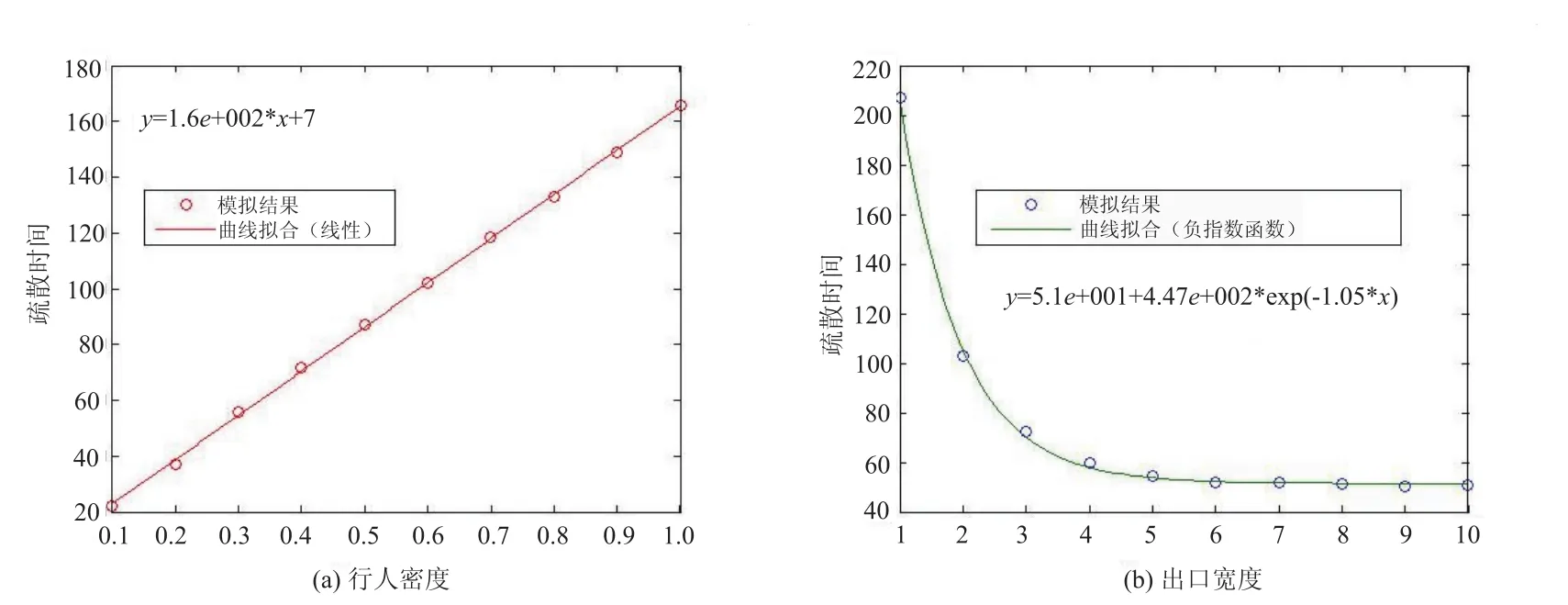
图6 曲线的拟合Fig.6 Curve fitting

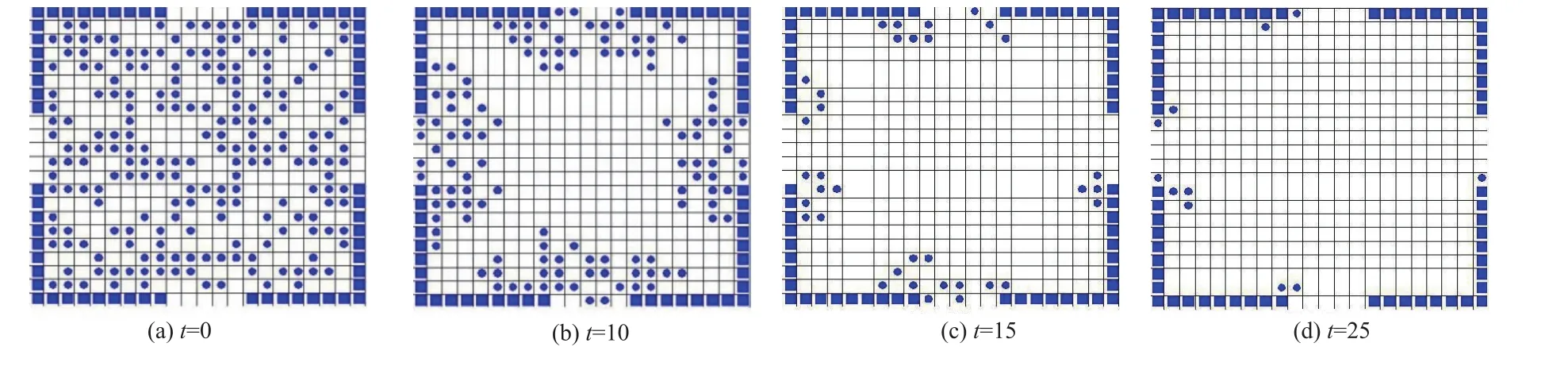
图7 行人的疏散过程W=20,L=5,K=0.5Fig.7 The snapshots of evacuation process while W=20,L=5,and K=0.5

4 研究结论

本文建立了包括方向参数、空格参数和感知参数在内的行人疏散动态参数模型,同时根据摩尔近邻的二维元胞自动机,构造了行人的移动规则并对行人疏散进行了相应的模拟.在本文所建立的模型中,考虑了出口周围的行人密度对疏散过程的影响,通过模拟和实验,以及与原模型的比较结果证明,这种改进是有效的,因为在对于门的选择上,除了对空间距离的要求以外,密度也是一个很重要的影响因素.与此同时,本文也考虑了行人分布、行人密度以及出口宽度对疏散时间的影响,我们发现疏散时间与行人密度呈线性关系,与出口宽度呈负指数函数的关系,并通过曲线的拟合,对所得的结论进行了验证.根据不同位置出口的设置,讨论了出口布局对疏散时间的影响,并给出了疏散空间最优布局,即门的最优宽度和最优位置.因此,本文所建模型对于行人疏散和实际建筑的设计具有指导意义,可以避免和减少人员伤亡.

[1] Yang L Z,Zhao D L,Li J,et al.Simulation of the kin behavior in building occupant evacuation based on cellular automaton[J].Building and Environment, 2005,40:411-415.

[2] Yuan W F,Tan K H.An evacuation model using cellular automata[J].Physica A,2007,384:549-566.

[3] Varas A,Cornejo M D,Mainemer D,et al.Cellular automaton model for evacuation process with obstacles [J].Physica A,2007,382:631-642.

[4] Yu Y F,Song W G.Cellular automaton simulation of pedestrian counter flow considering the surrounding environment[J].Physical Review E,2007,75:046-112.

[5] Weng W G,Chen T,Yuan H Y,et al.Cellular automaton simulation of pedestrian counter flow with different walk velocities[J].Physical Review E,2006,74:036-102.

[6] Song W G,Yu Y F,Wang B H,et al.Evacuation behaviors at exit in CA model with force essentials:A comparison with social force model[J].Physica A,2006,371: 658-666.

[7] Kirchner A,Klupfel H,Nishinari K,et al.Simulation of competitive egressbehavior:comparison with aircraft evacuation data[J].Physica A,2003,324:689-697.

[8] Nishinari K,Sugawara K,Kazama T.Modelling of selfdriven particles:Foraging ants and pedestrians[J]. Physica A,2006,372:132-141.

[9] Yue Hao,Shao Chun-Fu,Yao Zhi-Sheng.Pedestrian evacuation flow simulation based on cellular automata [J].Acta Physica Sinica,2009,58(07):4523-4530.

Simulation of Pedestrian Evacuation Based on a Dynamic Parameters Model

LI Te-lang1,3,ZHANG Xi1,ZHU Nuo2,CAO Wei1,ZHENG Pan2
(1.School of Traffic&Transportation,Beijing Jiaotong University,Beijing 100044,China; 2.China Academy of Civil Aviation Science and Technology,Beijing 100028,China; 3.State Tobacco Monopoly Administration,Beijing 100045,China)

A dynamic parameters model is presented based on cellular automata.The dynamic parameters: direction-parameter,empty-parameter and cognition-parameter are formulated to simplify tactically the decision-making process of pedestrians,which can reflect the pedestrian judgment on the surrounding conditions and decide the pedestrian's choice of action.Simulation of pedestrian evacuation and pedestrian moving rules are established,according to two-dimensional cellular automaton Moore neighborhood.The simulation results of the improved and previous models are compared and analyzed.In the improved model, the impact of the pedestrian density around exits in evacuation is considered,the simulation results prove that this improvement makes sense.At the same time,the effects of pedestrian distribution,pedestrian densityand exits width on the evacuation time are discussed,giving the optimal exit layout.The improvement of the CA model is useful for further study,it is instructional significant for pedestrian evacuation,avoiding or reducing the number of injuries.

traffic engineering;pedestrian evacuation;cellular automata;empty-parameter;cognitionparameter;direction-parameter;evacuation time

U491

: A

U491

A

1009-6744(2013)05-0042-06

2013-03-21

2013-06-07录用日期:2013-06-13

国家自然科学基金资助项目(71071013);中央高校基本科研业务费专项资金资助(2011YJS241).

李特朗(1977-),男,湖南益阳人,博士生.

*通讯作者:xizhang@bjtu.edu.cn