城市干线道路交通拥挤态势的监测

弓晋丽,彭贤武

(1.长沙理工大学交通运输工程学院,长沙410114;2.三一重工股份有限公司,长沙410100)

城市干线道路交通拥挤态势的监测

弓晋丽*1,彭贤武2

(1.长沙理工大学交通运输工程学院,长沙410114;2.三一重工股份有限公司,长沙410100)

以城市干线道路交通拥挤态势监测为目的,设计基于定点检测数据的异常监测系统.获取交通流基础数据(流量、速度、占有率)后,使用模糊C-均值聚类算法将定量数据转化为交通定性状态(拥挤或畅通).以此为基础,系统使用时间序列分形分析法确定交通拥挤态势指数;以序列模式相似性度量法和凝聚分层聚类法进行常规运行模式的辨识;并使用基于距离的异常模式变点识别法实时监测交通拥挤态势是否偏离常规运行模式,以此确定系统是否存在异常.以上海南北高架东侧11天的定点检测数据为例进行实证分析,监测得到了9月30日异常模式集中分布在中午12∶10-13∶20、13∶40-14∶30和下午17∶10-17∶15时间段内.

交通工程;拥挤态势;时间序列;异常监测;定点检测数据

1 引 言

当交通拥挤成为城市交通的常态后,如何实时监控城市交通日常运行中交通拥挤随着时间的发展变化情况,避免大面积拥堵的发生变得尤为重要.城市交通干线(快速路和主干路)承担了大量的交通量,在整个路网中具有关键性的作用,对干线交通拥挤发展态势的监测能够为预防路网的大面积拥堵做出预警.

国内外学者对交通拥挤监测问题进行了广泛研究.国外形成了以美国、日本和欧洲的各个机构和学者为代表的研究阵营,国内也有多所大学的多名学者进行了许多相关的研究[1-4].受问题本身研究对象(城市道路、交叉口、高速公路、快速路、路网)应用主体(出行者、交通管理者、规划设计人员)和数据条件(浮动车数据、环形监测线圈、视频采集等)的复杂性等因素影响,已有各种交通态势的描述和监测方法的应用范围都具有较强的针对性.随着ITS技术的发展,城市干线道路上布置了大量的检测线圈.如何从这些线圈检测到的数据中获取交通拥挤态势演变信息,对有可能引发路网大面积拥堵的干线道路异常状态做出预警,成为有意义的研究课题.本文以城市干线道路的交通拥挤整体发展态势为研究对象,将时间序列数据挖掘法应用于定点检测数据(流量、速度和占有率)采集系统的历史数据库和实时数据序列的分析中,实现监测对象交通异常发生时刻和严重程度的报警,为交通管理者和交通出行者提供服务.

2 城市道路模型化表示

根据检测线圈布设位置,可将道路划分为不同的路段,作为系统研究的“基本单元”.在得到环形检测线圈获得的流量、速度和占有率数据后,先使用模糊C-均值聚类算法,根据流量-速度-占有率关系对道路断面进行交通状态判别,区分畅通状态和拥挤状态(图1)[5];然后定义“失效路段”为满足上下游断面同时处于拥挤状态的路段,并统一将不满足上述条件的路段称为“畅通路段”(图2).

图1 交通状态模糊C-均值聚类Fig.1 Fuzzy C-means for traffic qualitative state

图2 城市道路模型化表示Fig.2 Model of city road

3 拥挤态势描述指标

2001年Chen等[6]采用车公里长度(Vehicle Distance Traveled,VDT)、车小时长度(Vehicle Hours Traveled,VHT)、总延误(Total Delay,TD)、效率损失(Productivity Loss,PL)等4个指标作为基于定点数据评价交通运行性能指标.为度量干线道路拥挤严重程度,本文在此基础上定义以下集计指标集.

(1)失效性度量指标.

式中 Num()——集合计数函数;

N——路段划分总数;

k——检测时间间隔数,一般以5 min或15 min为一个间隔;

B(k)——k时间间隔内失效路段集合.根据定义,任意时间间隔内的失效路段数Ns小于等于道路路段划分总数N.

(2)失效度度量指标集.

式中 TVH(k)——k时间间隔内干线总车小时长度,单位为veh·h,表示统计时间间隔内道路上所有车辆占用道路的总时长;

TVM(k)——k时间间隔内干线总车公里长度,单位为veh·km,表示统计时间间隔内道路上所有车辆行驶里程总和;

TD(k)——k时间间隔内干线总延误,单位为veh·h,表示由于“失效”导致道路上行驶车辆产生的延误总和;

TPL(k)——k时间间隔内干线总损失能力,单位为km·h,表示由于“失效”导致路段上通行能力的总损失量;

L——路段集合;

ρi(k)——k时间间隔内基本单元i的密度,单位为veh/km;

Vi(k)——k时间间隔内基本单元i的空间平均速度,单位为km/h;

vi——基本单元i的自由流速度,单位为km/h;

qi(k)——k时间间隔内从基本单元i流出的流量,单位为veh/h;

QM,i——基本单元i的通行能力,单位为veh/h;

Δxi——基本单元i的长度,单位为km; Ts——采样周期(时间间隔),单位为h.

实际中,由于环形检测线圈只能得到流量q、时间平均速度vt,上述计算中使用到的空间平均速度V和密度ρ采用以下公式转换[7]:

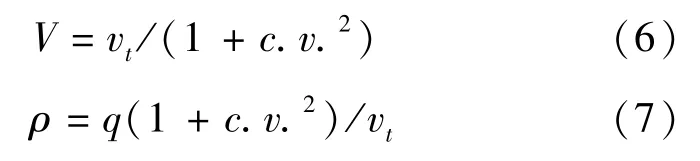
式中 c.v.——变异系数,取值范围为[0.08,0. 17].

上述多个指标构成了交通拥挤严重程度评价的时间序列指标集,可作为下文确定“交通拥挤态势指数”的基础指标集.

4 拥挤态势监测系统设计

4.1 拥挤态势描述指数确定模块

在提出上述定性和定量指标集后,需对它们进行趋势一致性验证,以便确定能从定性角度与定量角度对干线拥挤态势做出准确描述的综合性指标.在时间序列数据挖掘算法中,R/S分析法[8]是一种用于验证时间序列是否具有一定趋势性的方法.运用该方法可计算各时间序列的Hurst指数,得到的结果越接近表明两组时间序列的变化趋势越一致.下文简要介绍该方法的计算过程[8].

给定一个时间序列的N个连续观测值X(1), X(2),…,X(N),均值记为.在此序列基础上可以得出另一个序列Y,其中

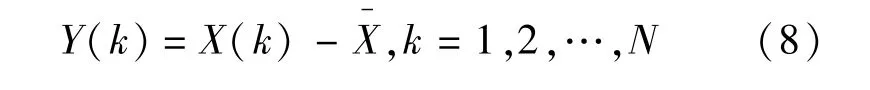
令

则包括N个样本的连续时间序列的Hurst指数H可按式(11)确定.如N=100,此时n可以取2、4、5、10、20、25、50等7个数,先求解(R/S)n,再由(R/S)n对n回归求得H.

式中 n——原始序列被等分后子序列的长度,其值为[1,N]间能被N整除的正整数;

R——原始时间序列的子序列X1,X2,…,Xn经调整后的极差;

S——原始子序列标准差;

H——Hurst指数,值介于0到1之间,H愈接近1,持续性愈强,H愈接近0,反持续性愈强;

c——常数.

运用上述方法分别计算4个失效度指标和失效性指标时间序列的Hurst指数,找到定量与定性指标中结果最接近者作为拥挤态势指数,流程如图3所示.

4.2 拥挤态势模式辨识模块

当确定了“拥挤态势描述指数”后,将一段时间内的一系列拥挤态势指数时间序列作为输入进行本模块的计算.本模块旨在从大量的历史存档数据中发现指标时间序列变化趋势的模式,建立交通拥挤态势日常模式,作为监测交通状态是否偏离常规模式的比较基准.时间序列模式被定义为一个相似时间序列的集合,模式辨识本质是实现以天为单位的具有相似性变化趋势的交通拥挤态势指数时间序列的聚类.具体方法:

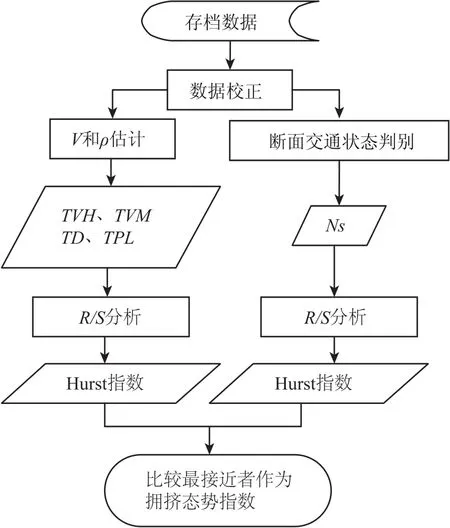
图3 交通拥挤态势指数确定流程图Fig.3 Flow-chart of traffic state evolution index determination

(1)以一天为一个样本,计算样本两两之间的形状相似性距离.“模式距离[9]”可从形状上度量样本的相似度,下文简要介绍其计算方法.令m= (X(k+1)-X(k))/Ts,则定义时间序列X= {X(1),X(2),…,X(n)}的模式XM为

式中 XM={-1,0,1}对应三种趋势类型{上升,保持,下降};th表示“保持”趋势斜率阈值,为接近0的某一较小值.在此基础上定义时间序列X和Y之间模式距离DM(X,Y)为

式中 n表示时间序列间隔个数.根据定义式易知,X和Y的模式距离DM(X,Y)∈[0,2].

(2)由于凝聚分层算法在进行交通流时间序列分类时具有优越性[10],本文使用该方法根据模式距离从形状和严重程度上实现交通拥挤态势指数时间序列的有效分离.

(3)计算各个样本的交通拥挤态势指数时间序列累计值,获得聚类结果中平均累计值最大的一类,将其称为“拥挤最严重类”,做为判断系统是否发生异常的监测基准类.

4.3 拥挤态势异常实时在线监测模块

拥挤态势“异常”是指交通运行状态随着时间的变化偏离了常规运行规律,也即交通系统运行内在机制发生了与常规状态不同的改变.以上述模块得到的“拥挤态势常规模式”为比较基准,本模块以天为单位将实时获取的数据与常规模式比较以实现交通拥挤态势的实时监测.具体方法如下所述.

2000年Knorr[11]提出了基于距离的异常模式(Distance-based Outliers)的定义:“T中某子序列O与同数据库中子序列p比较,其距离DB(p,O)大于阈值D,则认为O为异常序列”.以上述概念为基础,本文基于相似性度量距离定义时间序列“异常因子(Outlier Factor,OF)”,用来描述模式异常的程度,并用于检测某段时间内序列模式是否异常.

(1)异常因子的定义.

对于等长的待检测序列q和比较基准类PB中某一序列p,异常因子OF(q):

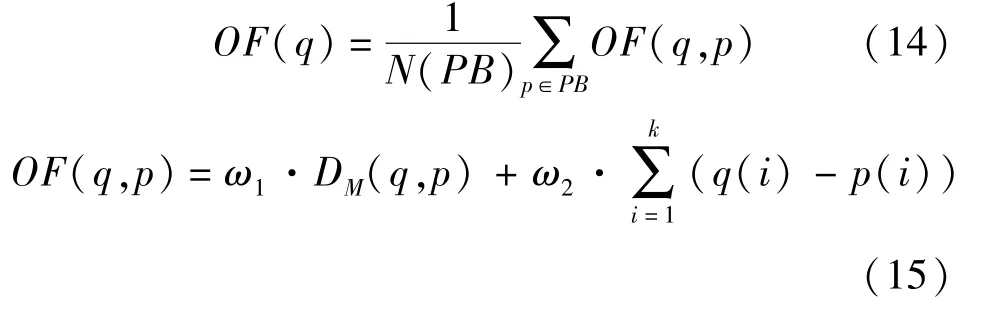
式中 OF(q,p)——序列q和比较基准类PB中某一序列p间的模式相似性距离;

N(PB)——基准类PB所包含的样本个数;

q(i)和p(i)(i=1,2,…,k)——分别为序列q和p第i个值;

ω1和ω2——分别为形状相似距离和指标值偏离量的权重,表示它们对“异常因子”的贡献大小,二者满足等式ω1+ω2=1.

(2)基于滑动窗的异常模式实时检测算法.

滑动窗口是指在处理数据时只考虑最近序列,被用来获取当前数据流的特征信息.在滑动窗口内不仅有新数据连续到达,而且也会有旧数据过期[12].为进行定点数据的实时监测,本算法使用滑动窗技术,与基准中时间序列比较,将异常因子作为序列特征,如果异常因子增大,并超过给定阈值,则认为实时状态变化偏离历史模式较严重,需要作出预警.图4给出了算法流程,输入参数为实时检测序列X、监测基准类PB,输出为异常模式发生时刻及各个时刻异常因子的值.

图4 基于滑动窗的异常模式实时检测算法流程图Fig4 Flow-chart of distance-based outlier real-time detection algorithm

5 实例验证

以上海南北高架东侧路段为例,应用本文所设计系统进行实证分析.将2009年3月20日(周五)至3月29日(周日)白天6:00-19:00间定点检测数据作为历史数据进行模式辨识,选取同年9月30日同时段数据作为实时监测的对象.上述验证过程选用Matlab编写了相应的计算程序,并在Dell笔记本(CPU双核1.6 GHz,内存1 G)上实现.

5.1 R/S分析结果

利用R/S计算各拥挤态势指标的Hurst指数,结果如表1所示.

据表1,上述指标的Hurst指数均大于0.5,表明交通拥挤态势具有长期相关的特征,即整个演化过程整体上具有稳定的持续性.其中,TD与失效性指标的Hurst指数最为接近,因此,下文将TD作为“拥挤态势指数”.为比较方便,在下文的计算中,统一将“拥挤态势指数”指标进行了归一化处理.

表1 Hurst指数计算结果Table 1 Calculation results of Hurst index

5.2 常规运行模式辨识结果

对历史数据库中3月20日-3月29日6:00-17:00共计10个白天的检测数据进行了模式辨识,结果如图5所示.

图5中横坐标表示时间,纵坐标表示指标值.由图可见,模式辨识首先将交通基本特征差异较大的工作日和周末序列进行了分离,并从形状上将3月26日线从工作日中分离,然后从剩下的工作日序列中实现拥挤最严重的3月27日序列分离,最后成功将拥挤较严重的3月20日(周五)与其他工作日分离.在此基础上计算各类样本的类内平均累计值,对各类拥挤严重度做出排序,结果如表2所示.据此,得到“类3({3月27日})”为拥挤最严重类,作为监测系统的比较基准.

图5 模式辨识结果Fig.5 Results of pattern discrimination

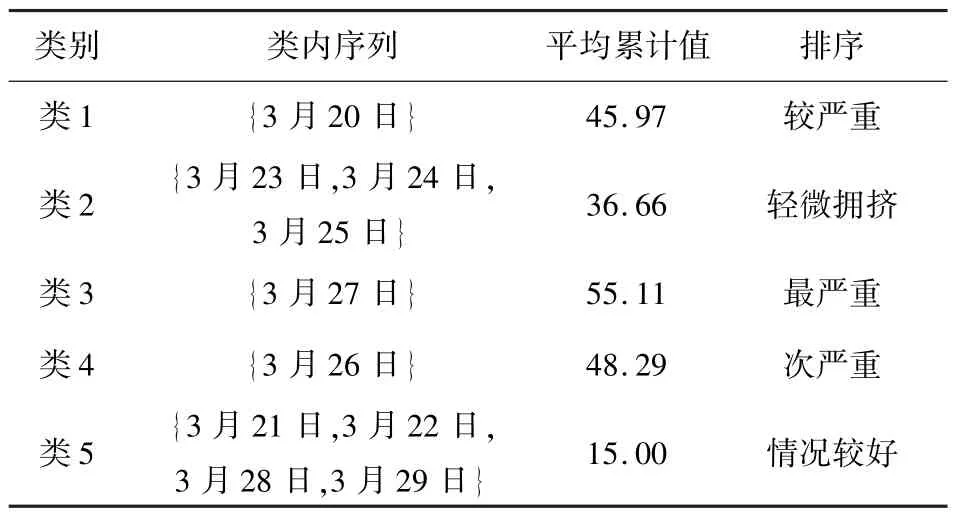
表2 拥挤严重程度排序Table 2 Traffic congestion sevrity sorting

5.3 异常检测结果

已知9月30日处于国庆放假的前一天,当天交通出行量大,上海市交通一度处于瘫痪状态,路网出现大面积拥堵.算法以该天为监测对象,检测当天交通拥挤态势的异常时刻.

(1)算法输入包括:实时检测对象X=9月30日6:00～19:00以5 min为间隔的拥挤态势指数时间序列;监测类基准类PB=3月27日6:00～19:00以5 min为间隔的数据,PB为1*156维矩阵;初始窗口l1=12,即从7:00开始监测;滑动窗长度l=12,即以一小时为滑动窗口.

(2)参数OFmax的标定:使用历史库中除3月27日外的9天数据标定OFmax,计算历史天内各个时刻的异常因子OF(q,t),并设OFmax为99.5%分位的统计量(图6),其值为0.41.

(3)检测结果分析.

根据异常监测算法,获得9月30日异常报警结果如图7所示.从图7中可以看到,当天异常模式集中在中午12:10-13:20、13:40-14:30和下午17:10-17:15时间段内,正是由于这些时间段内拥挤未得到及时消散,导致了9月30日长时间的持续性拥堵.

图6 异常因子经验累积分布函数图Fig 6 Experience cumulative distribution function diagram of Outlier Factor

图7 9月30日异常因子时变图Fig.7 Time changing diagram of outlier factor on September 30

6 研究结论

本文以城市干线道路交通拥挤态势异常监测为目的,设计了基于定点数据的监测系统.在使用实际道路检测数据验证后,得出的结论包括:

(1)为从定性和定量角度对交通拥挤发展变化趋势做出客观评价,由时间序列挖掘算法中R/S法确定TD为“拥挤态势指数”.实例中,各个拥挤态势描述指标的Hurst指数均大于0.5,表明交通拥挤的趋势变化具有较强的规律性,各天间交通拥挤态势变化具有相似性.

(2)基于模式距离的凝聚分层算法可实现交通拥挤态势模式相似性和差异性的辨识.在辨识结果基础上,利用各类内拥挤态势指数平均累计值实现各天拥挤严重度排序,确定实验数据中拥挤最严重类“3月27日”为异常监测的比较基准.

(3)定义了时间序列“异常因子(Outlier Factor,OF)”描述时间序列模式异常的程度,并将其作为序列特征设计了基于滑动窗的异常模式实时检测算法.实例中,以9月30日为监测对象,设置“异常因子”阈值为0.41,检测得到当天异常集中分布在中午12:10-13:20、13:40-14:30和下午17:10-17:15时间段内,测算结果符合当日的实际交通情形.

综上所述,本文研究成果可为交通管理者与交通出行者了解道路实时运行状况,掌握交通拥挤发生规律提供服务.但本文研究仅限于具备定点检测数据时对道路干线拥挤态势做出监测,未来可考虑使用数据融合技术扩展其他类型数据源(如浮动车数据),并可针对路网开展研究.本文的研究成果也有待结合更加具体的实际道路条件,推广应用于实际城市道路的监测与管理中,也有待于在应用中进一步实现功能的完善和方法的提升.

[1] Pravin Varaiya.California partners for advanced transit and highways(Path)[R].University of California, Berkeley,2004.

[2] Robert L Bertini,Steven Hansen,Spicer Matthews,et al.Portal implementing a new generation archived data user service in portland,oregon[C].12th World Congress on ITS,San Francisco,2005.

[3] 胡启洲,刘英舜,郭唐仪.城市交通拥堵态势监控的时空分布形态识别模型[J].交通运输系统工程与信息,2012,12(03):41-45.[HU Q Z,LIU Y S,GUO T Y.Space-time distribution model on state monitoring ofurbantrafficcongestion[J].Journalof Transportation Systems Engineering and Information Technology,2012,12(03):41-45.]

[4] 关伟,何蜀燕,马继辉.HMI—城市快速路发生交通拥堵的一个预警指标[J].交通运输系统工程与信息,2008,8(05):26-31.[GUAN W,HE S Y,MA J H.HMI:Prewarning index of traffic jam formation on urban freeway[J].Journal of Transportation Systems Engineering andInformationTechnology,2008,8 (05):26-31.][5] 弓晋丽,杨东援.基于检测线圈数据道路交通瓶颈分析[J].公路交通科技.2010,27(7):118-122. [GONG J L,YANG D Y.The road bottleneck analysis based on loop detector data[J].Journal of Highway and Transportation Research and Development.2010, 27(7):118-122.]

[6] Chao Chen,Karl Petty,Alex Skabardonis,et al. Freeway performance measurement system mining loop detector data[R].Transportation Research Record 1748.2001:96-102

[7] 胡小文,杨东援.城市快速道路交通流密度的估计[J].交通运输系统工程与信息,2008,8(03):79-82.[HU X W,YANG D Y.Estimation of traffic densityonurbanfreeways[J].Journalof Transportation Systems Engineering and Information Technology,2008,8(03):79-82.]

[8] 埃德加E彼得斯.分形市场分析[D].北京:经济科学出版社,2002.[Edgar E Peters.Fractal market analysis[M].Beijing:EconomicScience Press,2002.]

[9] 王达,荣冈.时间序列的模式距离[J].浙江大学学报(工学版),2004,38(07):795-798.[WANG D, RONG G.Pattern distance of time series[J].Journal of Zhejiang University(Engineering Science),2004,38 (07):795-798.]

[10] C Oller-Levet,F Klawonn,K-H Cho,et al.Fuzzy clustering of short time series and unevenly distributed Sampling[C].Proc of the 5the Int Symp on Intelligent Data Analysis.New York:ACM,2003.

[11] E Knorr,R Ng,V Tucakov.Distance-based outliers algorithms and applications[J].VLDB J,2000,8(3-4):237-253.

[12] P Domingos,G Hulten.Mining high-speed data streams [C].In Proceedings of the sixth ACM SIGKDD international conference on knowledge discovery and data mining,2000:71-80.

Monitoring the Evolution of Traffic on Main City Roads

GONG Jin-li1,PENG Xian-wu2
(1.School of Transportation Engineering,Changsha University of Science&Technology,Changsha 410114,China; 2.Sany Heavy Industry Co.,Ltd,Changsha 410100,China)

In order to monitor the evolution of traffic on main city roads,a fixed-point data monitoring system is devised.Firstly,after qualitative traffic data(flow,speed,and occupancy)are acquired,they are then translated into the traffic qualitative state(congested or uncongested)by Fuzzy C-means Clustering algorithm.Secondly,the Congestion Evolution Index is determined using Rescaled Range Analysis of data mining.Finally,by taking a sequence pattern similarity measurement and applying condensed hierarchical clustering methods,the routine pattern is distinguished.Consequently,real-time outlier detection is realized by a distance-based outlier detection algorithm.This algorithm was successfully applied based on 11 days of fixed-point data on the eastern segment of the Shanghai North-South expressway,it is concluded that the outliers distributed in 12:10-13:20,13:40-14:30 and 17:10-17:15 on September 30.

traffic engineering;traffic state evolution;time series;outlier detection;fixed-point data

U491.112

: A

U491.112

A

1009-6744(2013)05-0030-08

2013-03-28

2013-06-10录用日期:2013-06-20

863计划项目(2007AA12Z242);国家自然科学基金项目(50738004);公路工程教育部重点实验室开放基金资助项目(kfj120106).

弓晋丽(1983-),女,山西省文水县人,讲师,工学博士.

*通讯作者:gjl2001cd@126.com