不确定需求下物流企业运输合作博弈模型研究

何 伟,徐福缘

(1.上海理工大学管理学院,上海200093;2.安徽财经大学统计与应用数学学院,安徽蚌埠233030)

不确定需求下物流企业运输合作博弈模型研究

何 伟1,2,徐福缘*1

(1.上海理工大学管理学院,上海200093;2.安徽财经大学统计与应用数学学院,安徽蚌埠233030)

随着经济全球化和电子商务的快速发展,物流管理模式不断变革,物流企业联盟应运而生,合作运输是不确定需求市场下物流运输企业广泛使用的一种运输策略.本文研究了在合作运输策略下物流企业之间的运输合作问题,分别讨论了基于时间的合作运输策略和基于数量的合作运输策略下企业运输合作费用的分摊问题,建立了相应的运输合作博弈模型,利用合作博弈理论,将联合运输的成本分摊问题转换为费用分摊博弈问题.通过对企业联合运输行为的研究,证明该博弈为凹博弈,且核心非空,并设计了属于核心中的费用分摊方案.研究结果表明,合作不仅能够降低企业的成本,还能提高客户服务水平.最后,用数值例子验证了相关结论.

交通运输经济;合作运输;合作博弈;物流;费用分摊

1 引 言

随着经济的发展,人们的需求呈现多样化与小批量化且不确定的趋势,这对物流运输提出了更高的要求.同时电子商务的快速发展,给物流企业提供了巨大的发展空间,但也加剧了物流运输市场的竞争.在机遇与挑战并存的环境下,物流企业要想求生存、谋发展,就必须努力降低成本,提高客户服务水平,提高企业的整体竞争力.物流企业可以采用合作运输,即把随机到达的几个小订单合作成一次运输,降低运输成本,提高车辆的利用率,从而提高整体的竞争力[1].例如为汽车组装商运输零部件的物流运输企业可以将不同零部件供应商随机到达的零部件进行合作运输至组装工厂[2].这种策略适合于对运输提前期要求不是很高及不具有易腐性的产品,对于这些产品,当随着运输量的增加单位运输成本不会明显增加时,通过合作运输可以为每笔订单节约多达50%的运输成本[3].

虽然单个企业通过合并自己的运输订单可以降低成本,但当单个企业的需求较小,即企业订单的平均到达率较小时,合并订单时运输提前期会较大,此时客户的服务水平会较低.为了能在降低成本的同时保证客户服务水平,越来越多的企业寻求与其它企业进行物流信息化以加强运输合作,提高物流效率和服务水平、节约物流成本,进而增强企业的核心竞争能力[4].文献[5]分析了物流企业风险厌恶程度、联盟协同效应和各种成本系数等因素对物流企业投入和联盟协作的影响.物流企业之间的合作可以更好地实现协同效益(如充分利用车辆资源),降低运输成本和运输提前期,提高资源的利用率,提高总体的服务水平.使用合作运输策略的企业通过合作将自己的订单与其它企业的订单进行合并,更好地发挥了合作运输的优势,达到需求的规模经济效益,在降低成本的同时保证客户的服务水平.

目前合作运输的研究对整车合作运输关注较多,主要集中在不同运输线路的组合优化与费用分摊,如Ergun等[6,7],Ozener等[8].对于物流运输合作,Dai和Chen[9,10]分别研究了物流企业通过拍卖机制进行合作和物流运输企业合作优化问题及费用分摊问题.Liu等[11]针对物流运输企业合作提出了一种WRSM费用分摊机制.Hernández[12]等研究了在参与合作的资源是动态的情况下物流运输合作的优化算法.Krajewska等[13]以夏普利值作为物流运输企业合作的费用分摊方案,并以实际案例分析合作所能产生的利润.以上关于物流运输合作的研究都假设需求是确定的,没有考虑需求的不确定性.Zhou[14]利用仿真的方法分析了不确定需求条件下物流运输合作的策略选择,但是没有考虑合作后的费用分摊问题.Yilmaz等[15]分析了不确定需求市场下,物流运输企业之间的合作,考虑了参与合作的物流企业的订单在不同装运点进行重新分摊的问题,将该问题模型化为马尔科夫决策过程,并讨论了托运人合作的费用分摊方案.与以上研究不同,本文考虑了在不确定需求市场下,使用合作运输策略的企业间的合作问题.

合作运输主要有三种策略,基于时间的合作运输策略(简称时间策略),基于数量的合作运输策略(简称数量策略),以及基于时间和数量的合作运输策略(简称时间数量策略)[14].时间策略是指企业预先设定一个时间运输周期T,每隔时间T合并一次运输订单;数量策略是指企业预设定一个运输量的临界点q,当随机到达的订单的总运输量第一次超过这个临界点时合并订单进行运输;时间数量策略是指预先设定一个时间周期T和运输量临界点q,当订单的总运输量超过临界点或者订单的最长等待时间达到T时,合并订单进行运输.

基于时间的合并运输策略和基于数量的合并运输策略就是要确定最优的运输周期T或者最优的运输量临界点q使得单位时间的库存持有成本与运输成本之和最小.Cetinkaya等[2]利用更新理论分别对数量策略与时间策略下的合并运输进行了研究,并分别给出了在这两种策略下订单到达率及每笔订单的需求量满足泊松分布时的最优时间周期T和最优运输量q的数学表达式.本文基于时间策略与数量策略这两种合作策略,分别讨论企业合作的费用分摊问题,应用合作博弈理论,建立相应的合作博弈模型,证明了该博弈为凹博弈,且核心非空,并设计了属于核心中的费用分摊方案.

2 问题描述

本文考虑物流配送市场上有N={1,…,n}个企业,每个企业面对的需求都是随机的.对于企业i,设随机变量表示其第(j-1)个订单与第j个订单到达的时间间隔.且假设订单到达时间间隔和随机需求量相互独立.令1,且,则表示在时间段(0,t)内到达的订单数量.另设随机变量表示企业i第j笔订单的配送量.令,且,则表示总配送量达到q的订单数.假设{与随机变量序列相互独立,同时假设与都是泊松过程,其均值分别为,即相邻订单到达的时间间隔和每笔订单的配送量分别满足均值为的泊松分布[11].由于不同企业处在同一个配送市场中,其面对的订单具有同质性,因此可以假设各个企业面对的每笔订单的配送量服从相同的泊松分布,即假设对所有的.最后令表示在时间点t的累积总配送量.

3 物流企业联合配送策略

本节要解决的问题是要确定最优的配送周期T或者最优的配送量临界点q使得单位时间的库存持有成本与配送成本之和最小.下面分别分析时间策略下和数量策略下企业进行联合配送的情况.

3.1 时间策略下联合配送的最优配送周期

企业在一个周期内的成本包括配送成本和库存控制成本.设KD和KO分别表示每个企业每次配送的固定成本和每笔订单的处理成本,c表示企业每单位配送量的变动成本,h表示单位时间单位配送量货物的库存控制成本.由于泊松分布具有可加性,因此对于任意的企业集合E⊆N,当他们进行联合配送时,其总订单到达率满足参数为的泊松分布.在使用时间策略的情况下,他们共同决定服务周期TE使得总期望成本最小.因此,在时间策略下企业E在一个周期内的期望总配送成本TC为[1]

其期望总库存控制成本HC为

故企业联合配送时单位时间的总期望成本为

参与合作的企业共同决定最优的T*E使得单位时间的总期望成本最小.根据式(3)的一阶条件可得

将式(4)代入式(3)可得企业E配送合作时单位时间的总期望成本为

3.2 数量策略下配送合作的最优配送量临界点

在采用数量策略时,由于每笔订单配送量的随机性,通常实际的货物配送量要比选取的临界值q大,其实际的配送量为(q+E[Y2(q)]),其中E(Y2(q))表示实际配送量超出配送量临界点q部分的期望值,其值为μ.在一个配送周期内,到达订单的总配送量第一次超过配送量临界点q所用的平均时间为(q/μ+1)/λ.因此,当任意的企业集合E⊆N进行联合配送并采用数量策略时,其在单位时间的总期望成本为[1]

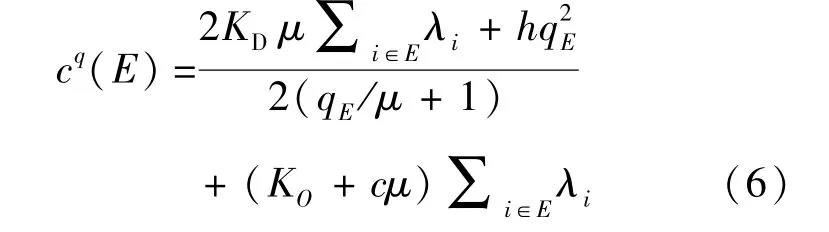
将式(7)代入式(6)可得企业单位时间的总期望成本为

4 企业物流配送合作博弈

4.1 时间策略下的配送合作博弈

本节主要探讨在时间策略下,物流配送企业是否应该合作,即合作能否带来好处。我们应用合作博弈理论,将时间策略下的配送企业的联合配送问题构造成时间策略下的配送合作博弈.

一个合作博弈可以定义为一个二元组(N, c),其中N={1,…,n}表示n个企业的集合,称为全联盟.函数c:2N→R为分派给任意非空联盟E⊆N的特征函数,且c(Ø)=0.如果对于博弈(N, c),对任意的E,R⊆N,E∩R=Ø,有

则博弈(N,c)满足次加性.若对任意的E⊆R⊆N{l},有

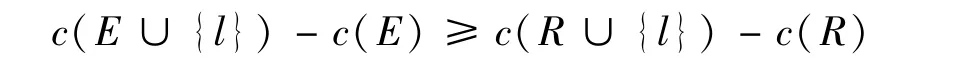
则博弈(N,c)是凹博弈,博弈(N,c)的核心分摊方案满足

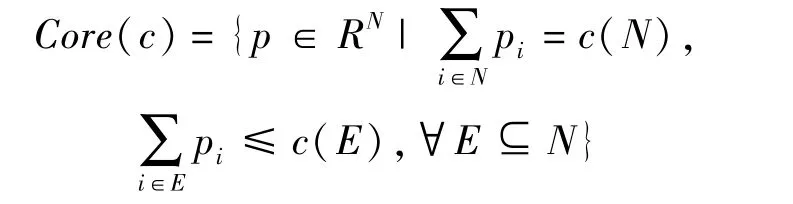
核心作为合作博弈的基本概念,对联盟成员之间的成本分摊提供了依据,核心分摊满足了个体理性和集体理性,是公平且合理的成本分摊方案.在核心中的费用分摊方案下,没有参与者愿意脱离大联盟单干或者组成小联盟,即大联盟是稳定的[16].

定义1 时间策略下配送合作博弈可以定义为二元组(N,cT),特征函数cT定义为c(Ø)=0,对任意的非空集合E⊆N

即特征函数是联盟在时间策略下实施联合配送时所能产生的最小总期望费用.

命题1 时间策略下配送合作博弈(N,cT)满足次加性,即对任意的E,R⊆N,E∩R=Ø,有cT(E)+cT(R)≥cT(E∪R).

证明由定义1知

从而有

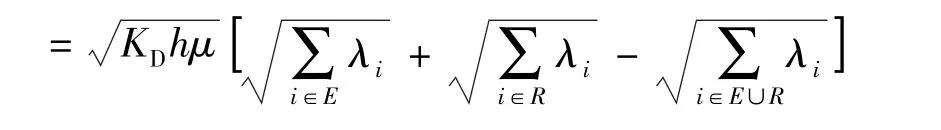
从而可得cT(E)+cT(R)≥cT(E∪R).

(N,cT)具有次加性意味着“整体小于部分之和”,即合作是有益的,合作可以带来成本的节约.由(N,cT)的次可加性可知对大联盟的任意划分,有.特别地,也即合作时联盟的总期望费用少于各企业独立配送时的期望费用之和,各企业最优策略是选择合作.

命题2 时间策略下配送合作博弈(N,cT)是凹博弈,即对任意的E⊆R⊆N{l},有cT(E∪{l})-cT(E)≥cT(R∪{l})-cT(R).

证明 由定义1可知

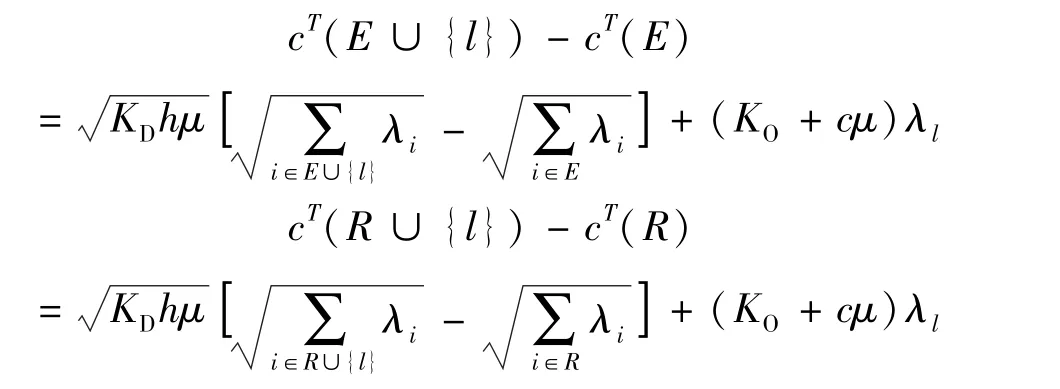
因此可得,

因此[cT(E∪{l})-cT(E)]-[cT(R∪{l})-cT(R)]≥0.

时间策略下的配送合作博弈(N,cT)的凹性意味着企业对某个联盟的边际费用随着联盟规模的增大而减小,即任意一个企业或联盟加入另一不相连联盟的动机随着联盟成员的增多而增大.

推论1 时间策略下的配送合作博弈(N,cT)满足平衡性,且具有非空核.

推论1说明存在使得大联盟稳定的费用分摊方案.由于时间策略下的配送合作博弈(N,cT)是凹博弈,因此其夏普利值、内核和核仁等经典的费用分摊解都在核心中[16].尽管如此,当联盟的参与企业增加时,这些解的计算复杂度成指数增加.因此提出一个即在核心中又便于计算的比例分摊解.该分摊方案按照企业订单到达率的比例分摊总成本.

证明 首先很显然∑i∈Nβi=cT(N),其满足预算平衡性.另外,对于任意的E⊆N,有

故β满足稳定性.

由于β在时间策略下的联合配送博弈的核心中,因此在该分摊方案下,大联盟是稳定的,没有企业愿意脱离大联盟单干或者组成小联盟.而且该分摊方案按照各企业订单到达率的比例进行成本分摊,订单到达率越大的企业,其分摊的成本也越大,这样不仅直观、易于理解和操作,又反映了公平性,因此在实际应用中具有可行性.

4.2 数量策略下的配送合作博弈

本节考虑数量策略下配送企业之间的联合配送问题.通过构建数量策略下的配送合作博弈来分析企业的合作情况.

定义2 数量策略下配送合作博弈可以定义为二元组(N,cQ),特征函数cQ定义为c(Ø)=0,对任意的非空集合E⊆N,有

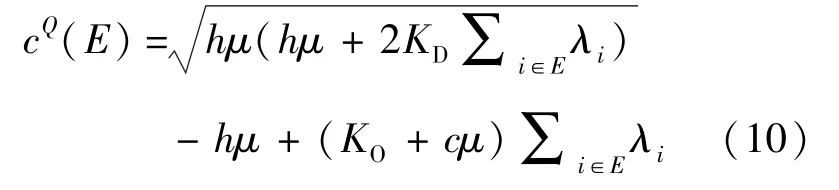
即特征函数是联盟在数量策略下实施联合配送时所能产生的最小总期望费用.

命题4 数量策略下配送合作博弈(N,cQ)满足次加性,即对任意的E,R⊆N,E∩R=Ø, cQ(E)+cQ(R)≥cQ(E∪R).

证明 由定义2知

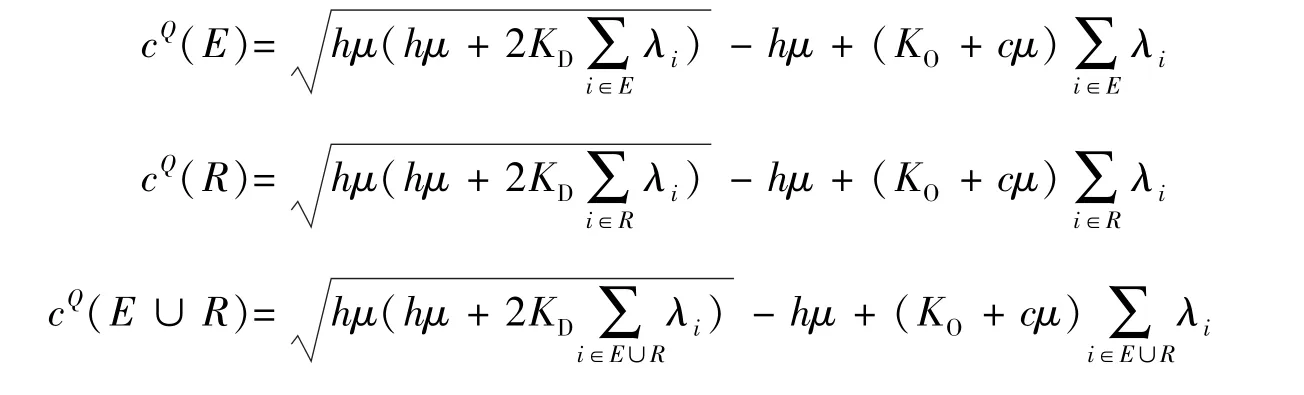
从而有

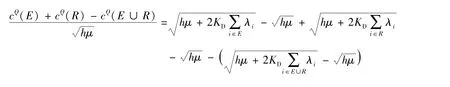
数量策略下配送合作博弈满足次加性说明在数量策略下,物流配送企业之间进行合作也是有利的,可以带来成本的节约.

命题5数量策略下配送合作博弈(N,cQ)是凹博弈.

证明由定义2知

因此,

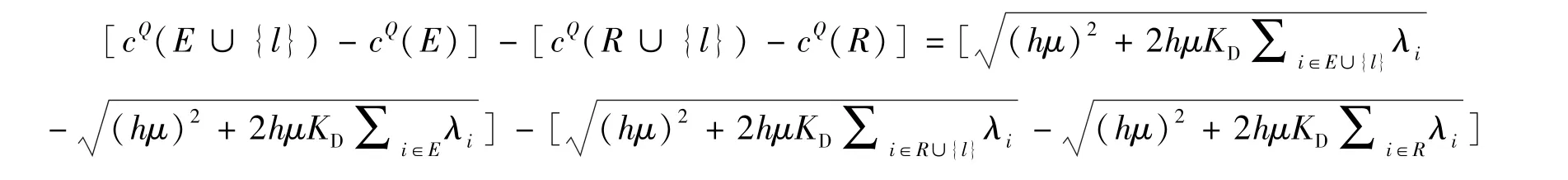
推论2数量策略下的配送合作博弈满足预算平衡性,且具有非空核.

核心非空说明存在使得大联盟稳定的费用分摊方案.针对数量策略下配送合作博弈特征函数的特点,提出一种数量策略下的配送合作博弈的核心中的费用分摊方案,其结构如下

该分摊方案的思想是,对于订单处理成本和变动配送成本按照企业订单到达率的比例进行分摊,因为这些成本本身是订单到达率的比例函数;对于库存控制成本与固定运输成本,首先对(-hμ)部分在各企业之间进行均分,然后对部分按照比例进行分摊,该比例由对hμ进行均分及对成本按照订单到达率进行比例分摊得到.所以,该分摊方案事实上也是一种比例分摊方法,具有公平合理且易操作性.

命题6由式(11)定义的费用分摊方案γ= (γ1,…,γn)属于数量策略下的配送合作博弈的核心.

证明很容易验证γ满足预算平衡性,即.下面证明该分摊方案满足稳定性.对任意的E⊆N,有

令函数

γ在数量策略下的配送合作博弈的核心中,说明在费用分摊方案γ下,大联盟是稳定的.由于费用分摊方案γ便于计算、易于理解,在实际应用中具有可操作性.

5 数值算例分析

假设市场上有三个物流运输企业.每趟运输的固定成本KD=420元,每笔订单的处理成本为KO=60元,运输的变动成本为c=120元/t,库存成本为h=10元/(t·h),每笔订单的平均重量为μ=7 t.订单平均到达率为(λ1,λ2,λ3)=(0.25, 0.30,0.45),在该需求参数下企业单独运输与合作运输的结果如表1和表2所示,表中c(N)表示联盟最优总期望成本,上标*代表最优解.

表1 企业单独运输时的结果Table 1 Outcomes when carriers work independently

表2 企业合作运输时的结果Table 2 Outcomes when carriers collaborate

通过比较表1与表2我们可以得到以下结论.

(1)不论是在数量策略下还是在时间策略下,合作都是有利的,都可以给每个企业带来成本节约,但在时间策略下节约的总成本比在数量策略下节约的成本要多.

(2)由表1可知,当企业单独运输时,数量策略分别是他们的最优策略,但是当他们合作时,时间策略是他们的最优策略.因此,合作可能导致最优策略的变化.一般来讲时间策略下客户的服务水平要高,因为运输周期要短.因此合作不仅可以带来成本的节约,还可以提高客户服务水平.

(3)由于运输量临界点q可以理解成企业选择的车型,即车辆容量.合作后联盟选择的运输量临界点q比企业单独运输时选择的q大,表示合作后联盟可以共同拥有容量更大的车辆,更能实现规模经济效应.如对于企业1来说,单独运输时其最优选择是容量为20 t以下的车辆,但是合作后他们的最优选择是容量为25 t以上的车辆.容量更大的车辆更能实现规模经济效应.因此合作可以促使资源更好地利用.

下面考虑不同订单平均达到率的情形,需求参数同上,计算结果如表3所示.

表3 企业合作运输时的结果Table 3 Outcomes when carriers collaborate

由表3可以发现,不论是在数量策略下还是在时间策略下,企业分摊的费用随着其订单的平均到达率的增加而增加.同时还发现订单的平均到达率越大,运输周期越短,最优的车辆容量越大.因此随着参与合作企业的增加,订单的总平均到达率增大,合作的优势越明显.因此物流运输企业应该积极寻求合作,提高资源利用率,实现规模经济,降低成本,提高客户服务水平,从而提高竞争力.

6 研究结论

合作运输的一个核心问题就是产生的总费用应该如何在参与者之间进行公平地分摊.本文考虑合作运输策略下物流运输企业之间的运输合作问题.利用合作博弈理论,将物流运输企业在时间合作运输策略下和数量合作运输策略下合作运输的费用分摊问题分别构造成运输合作博弈.首先证明了相应的博弈满足次加性,说明合作是有益的,然后证明了相应的博弈满足凹性,表明博弈的核心非空,并设计了属于相应核心中的分摊方案.同时本文的研究结果还表明,物流运输企业之间的合作运输不仅能够提高资源的利用率,降低企业的成本,还能提高客户的服务水平.本文的研究结论对实际生活中物流运输企业的合作提供了费用分摊方案和合作运输策略选择的指导,不仅具有理论意义还具有现实意义.

[1] Bookbinder J H,Higginson J K.Probabilistic modeling of freight consolidation by private carriage[J]. Transportation Research Part E,2002(38):305-318.

[2] Cetinkaya S,Bookbinder J H.Stochastic models for thedispatchofconsolidatedshipments[J]. Transportation Research Part B,2003(37):747-768.

[3] Higginson J K,Bookbinder J H.Markovian decision processes in shipment consolidation[J].Transportation Science,1995,29(3):242-255.

[4] 卫振林,张艳.物流信息化服务方式的博弈研究[J].交通运输系统工程与信息,2011,11(2):39-43.[WEI Z L,ZHANG Y.Game theory analysis on service mode of logistics information[J].Journal of Transportation Systems Engineering and Information Technology,2011,11(2):39-43.]

[5] 徐扬,申金升,王传涛,等.物流联盟的形成机理与协作博弈研究[J].交通运输系统工程与信息, 2011,11(2):21-26.[XU Y,SHEN J S,WANG C T, et al.Formation mechanism and cooperation games of logistics alliance[J].Journal of Transportation Systems Engineering and Information Technology,2011,11 (2):21-26.]

[6] Ergun O,Kuyuzu G,Savelsbergh M.Reducing truckload transportationcoststhroughcollaboration[J]. Transportation Science,2007(41):206-221.

[7] Ergun O,Kuyuzu G,Savelsbergh M.Shipper collaboration [J].Computers&Operations Research,2007(34): 1551-1560.

[8] Ozener O O,Ergun O,Savelsbergh M.Lane-exchange mechanisms for truckload carrier collaboration[J]. Transportation Science,2011,45(1):1-17.

[9] Dai B,Chen H.A multi-agent and auction-based framework and approach for carrier collaboration[J]. Logistics Research,2011(3):101-120.

[10] Dai B,Chen H.Profit allocation mechanisms for carrier collaboration in pickup and delivery service[J]. Computers&Industrial Engineering,2012(62): 633-643.

[11] Liu P,Wu Y,Xu N.Allocating collaborative profit in less-than-truckload carrier alliance[J].Journal of Service Science&Management,2010(3):143-149.

[12] Hernández S,Peeta S,Kalafatas G.A less-thantruckload carrier collaboration planning problem under dynamic capacities[J].Transportation Research Part E,2011(47):933-946.

[13] Krajewska M A,Kopfer H,Laporte G,et al.Horizontal cooperation among freight carriers:Request allocation and profit sharing[J].Journal of the Operational Research Society,2008(59):1483-1491.

[14] Zhou G,Hui Y V,Liang L.Strategic alliance in freight consolidation[J].Transportation Research Part E,2011(47):18-29.

[15] Yilmaz O,Savasaneril S.Collaboration among small shippers in a transportation market[J].European JournalofOperationalResearch,2012(218): 408-415.

[16] 董保民,王运通,郭桂霞.合作博弈论——解与成本分摊[M].北京:中国市场出版社,2008.[DONG B M,WANG Y T,GUO G X.Cooperative game theory-solutions and cost sharing[M].Beijing:China Market Press,2008.]

Game Model of Enterprises'Logistics and Transport Cooperation with Uncertain Demands

HE Wei1,2,XU Fu-yuan1
(1.Business School,University of Shanghai for Science and Technology,Shanghai 200093,China; 2.School of Statistics and Applied Mathematics,Anhui University of Finance and Economics,Bengbu 233030,Anhui,China)

The rapid development of economic globalization and electronic commerce has brought huge transformation of the logistics business management pattern.The theory of logistics alliance arose accordingly. Cooperative transportation is widely used by logistics enterprises with stochastic demand.This paper focuses on cooperative transportation among logistics enterprises under shipment cooperation policy.The cost allocation problem of combining transport policy among enterprises is converted into a cost allocation game based on the cooperation game theory under time policy shipment consolidation and quantity policy shipment consolidation, respectively.Analysis of enterprises'behaviors proves that the cost allocation game is concave,and has nonempty core.The results show that cooperation among enterprises not only reduces the cost of each carrier, but also enhances customer service level.And then the findings are illustrated by a numerical example.

transportation economy;cooperative transportation;cooperative game;logistics;cost allocation

F273.1

: A

F273.1

A

1009-6744(2013)05-0022-09

2013-03-26

2013-04-28录用日期:2013-05-07

国家自然科学基金(71171135,71071001);上海市一流学科项目资助(S1201YLXK);上海市研究生创新基金项目资助(JWCXSL1301);教育部人文社科项目资助(13YJC840035).

何伟(1981-),男,安徽来安人,博士生.

*通讯作者:xufy@usst.edu.cn