基于GM(1,1|τ,r)模型的城市道路短时交通流预测

郭 欢,肖新平*,Jeffrey Forrest

(1.武汉理工大学理学院,武汉430063；2.宾州州立SR大学数学系,PA 16057,USA)

基于GM(1,1|τ,r)模型的城市道路短时交通流预测

郭 欢1,肖新平*1,Jeffrey Forrest2

(1.武汉理工大学理学院,武汉430063；2.宾州州立SR大学数学系,PA 16057,USA)

充分考虑城市道路交通系统中交通流存在的延迟性和非线性,本文基于灰色GM(1,1|τ,r)模型对城市道路短时交通流进行建模预测.首先,通过建立城市交通路段上交通流量大于通行能力时的速度-流量关系,得到交通系统延迟时间τ的计算模型.再针对交通流存在的非线性特征,以模型的预测效果最优为目标,建立关于非线性因子的优化模型并利用粒子群算法寻找最佳的非线性参数r.最后对武汉市友谊大道某一路段进行交通实验,将灰色GM(1,1|τ,r)模型的预测结果与灰色GM(1,1)模型和支持向量机进行比较.结果表明,GM(1,1|τ,r)模型的预测精度有明显的提高,能为智能交通系统的管理和控制提供及时可靠的信息资源.

城市交通;GM(1,1|τ,r)模型;短时交通流预测;速度-流量模型;延迟时间;非线性因子

1 引 言

随着我国改革开放不断深入,城市化进程不断加快,交通事业飞速发展,城市交通拥挤和堵塞愈演愈烈,交通事故和环境污染日益严重,交通问题已成为制约城市发展的瓶颈.城市交通问题迫切需要治理,其中智能交通系统是缓解城市交通问题的有效手段之一.智能交通系统[1]一般由多个子系统组成,然而,所有这些子系统运行的前提是能够利用所采集的历史数据对未来时段的交通流做出连续、同步、准确的预测.道路短时交通流预测是实现交通信息服务、交通控制与诱导的前提和关键,是智能交通系统的重要组成部分,交通流量预测结果的好坏直接关系到交通信息的服务水平和交通控制与诱导的效果.因此,利用有效的短时交通流预测方法,从所获得的信息中准确快速地预测道路交通流状态,是当前智能交通系统发展的急需,具有重要的现实意义.

近年来,学者们在该领域进行了大量的研究, Queen和Albers[2]为预测交通流提出多变量贝叶斯动态模型.Ghosh和Basu等[3]用贝叶斯方法对SARIMA模型进行参数估计,进而预测交通流.Xie和Zhao等[4]提出了高斯过程模型,因为模型在泛化性上表现出显著优势,在交通流建模和其它时间序列分析中得到特别的关注.Xue和Shi[5]证明混沌现象在交通流中的存在性,通过对交通流每5分钟采样,以此为基础预测短时交通流比传统统计式方法具有较高的精度.杨兆升[6]基于径向基神经网络模型对交通流进行预测,但其存在训练所需样本数量较多的问题.Huang和Sadek[7]受人类记忆的启发研究了一种新的智能方法用来对短时交通流进行预测.

由于自然界环境的影响不确定(能见度、风向和温度等),以及人为因素的原因(如交通事故、突发事件、司机的个人心理状态等),交通流系统存在非线性特征.实际交通流系统中滞后效应也是普遍存在的,即系统在时刻t的输入不仅影响系统在时刻t的输出及其变化率,也将影响到t时刻以后系统的输出和变化率.常见的现象如:一个路口发生交通拥堵,可能其下游路口仍交通顺畅,过一定时间后下游路口也发生交通拥堵,这就表现为交通系统的延迟效应.但是,目前短时交通流的预测方法很少周全考虑交通流的非线性和延迟性,那就不能根据交通流的实际特征建立模型进行预测,也就不能提供合理有效的交通流信息,这将会影响智能交通系统的正面效应.

灰色系统理论[8]是邓聚龙教授在20世纪70年代末80年代初提出的用于研究不确定系统的理论,其中灰色模型已经成为很重要的预测方法[9].但是,最初的灰色模型没有考虑延迟性和非线性,而且方程大多是线性的,发展系数也限定在一定范围内.在2002年,邓聚龙[10-12]教授突破传统GM(1,1)中灰指数率局限在(-2,2)且序列满足线性的约束,提出了非线性GM(1,1| τ,r)模型,其中τ代表延迟时间,r是随着时间变化的灰输入次数(即非线性参数).Jiang[13]基于GM(1,1|τ,r)模型提出了移动目标分割算法,此算法利用图像序列固有的短时信息,从序列图像中提出移动目标.Huang[14]用GM(1,1|τ,r)模型在同时考虑推测时间和需求强度的情况下预测分析港口如何利用有限资源来提高竞争能力.由于交通流具有明显的灰色系统特征[15],本文利用充分考虑延迟性和非线性的灰色GM(1,1 |τ,r)模型对交通流进行预测,其中延迟因子τ由交通系统中的三参数关系确定,非线性因子r由粒子群算法寻优得到.

2 基于GM(1,1|τ,r)模型的城市道路短时交通流预测

2.1 GM(1,1|τ,r)模型及其相关性质

定义1 设X(0)=(x(0)(k)),k=1,2,…,n为原始数据序列,X(1)=(x(1)(k))是X(0)的一次累加序列,Z(1)=(z(1)(k))是X(1)的背景值,灰色模型GM(1,1|τ,r)为

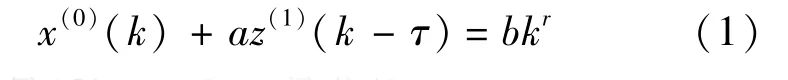
式中 τ是延迟因子；r是非线性因子.

记

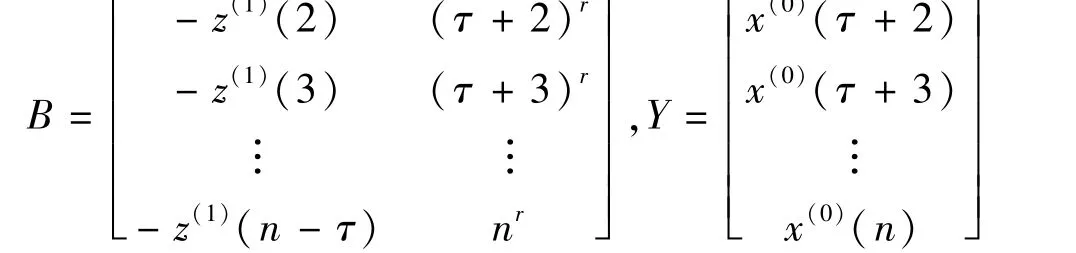
则参数a,b由最小二乘法得到

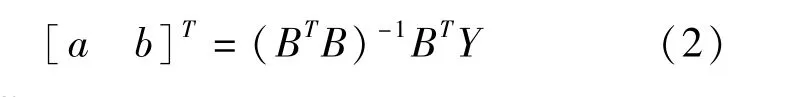
更进一步,令

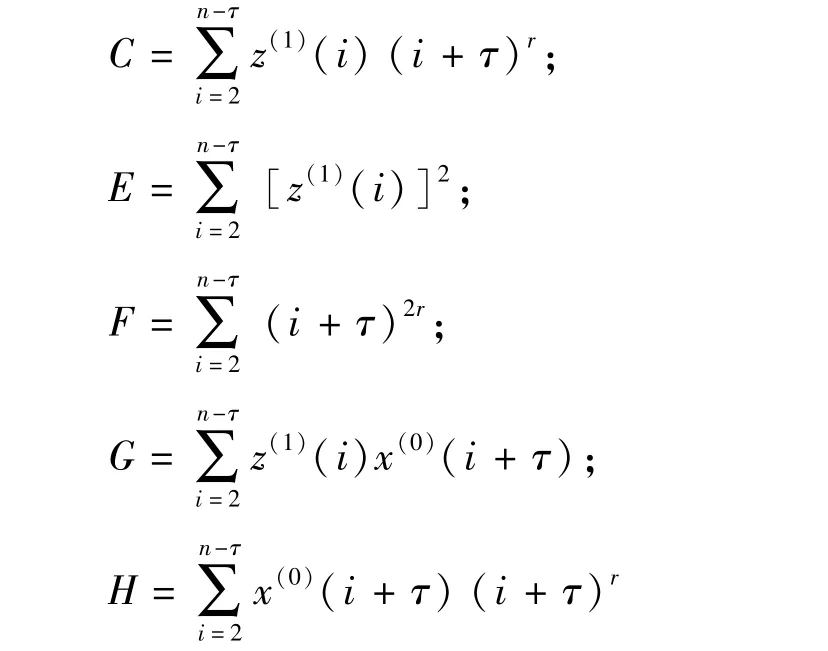
有

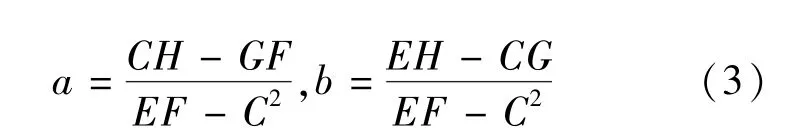
交通流量一般都很大,即使以5分钟为一个时间间隔,采集的流量值也达到三位数,这在实际建模预测的计算过程中,很容易出现奇异矩阵和计算误差.为克服该类现象,通常需要对原始数据进行数乘变换[16],但数乘变换是否会改变GM(1,1|τ, r)模型的预测精度,显然需要深入研究.

设x(0)(k),k=1,2,…,n为原始序列,那么x′(0)(k)=ρx(0)(k),k=1,2,…,n(ρ为常数,且ρ≠0)是数乘变换,常数ρ是数乘值.经过数乘变换后,模型的参数记为a′,b′,可得如下结论.

定理1 设[a b]T,[a′ b′]T是分别建立在原始序列x(0)(k)和数乘变换序列x′(0)(k)上GM(1,1|τ,r)模型的参数向量,x′(0)(k)= ρx(0)(k),则有a′=a,b′=ρb.

证明 如果x′(0)(k)=ρx(0)(k),k=1,2,…, n,有

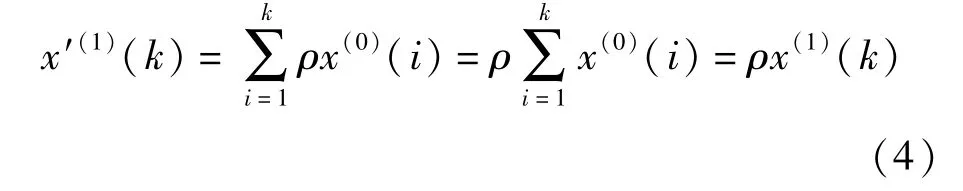
那么C,E,F,G,H的分别变化为

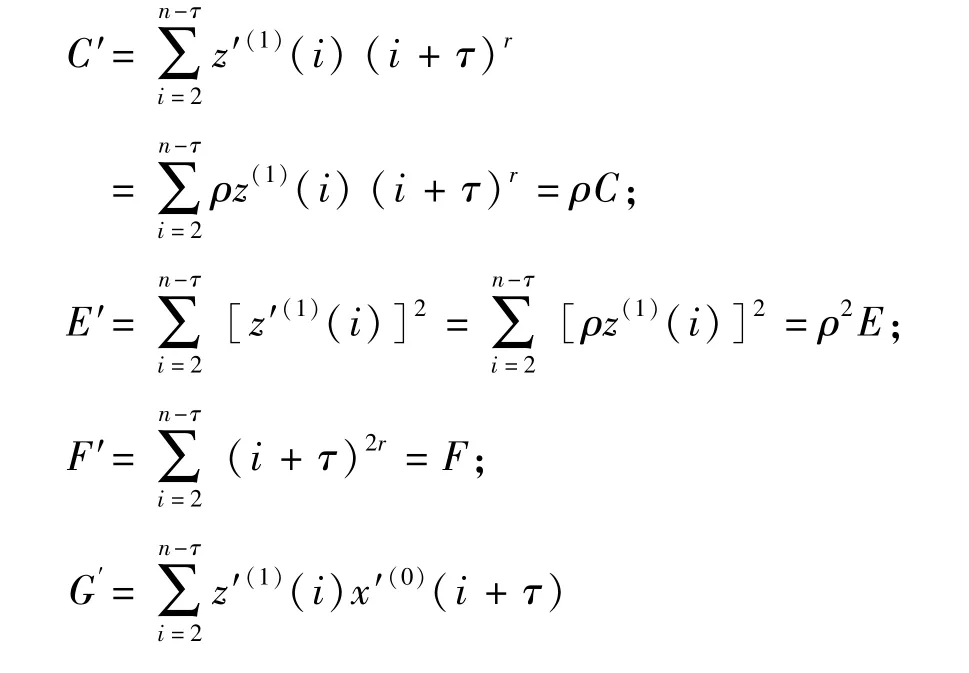
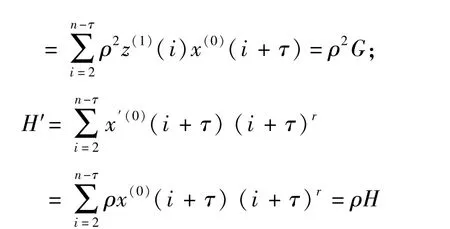
这里C′,E′,F′,G′,H′分别代表原始序列变换后所得模型的参数,可以得到

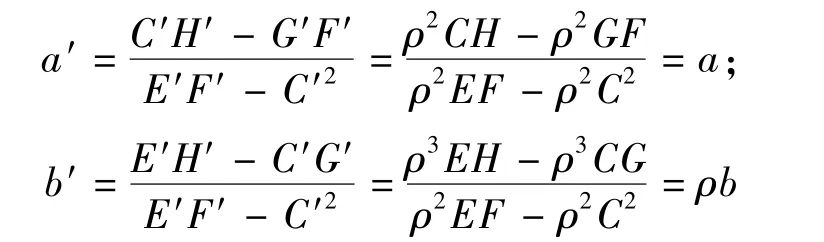
上述结果说明经过数乘变换,模型的发展系数不发生改变,即模型预测值的趋势不变.

2.2 交通系统延迟时间的确定

当某时段内,路段上的交通量大于该路段通行能力时,根据经典的速度-流量模型(Green-shields抛物线模型,见图1),显然车流速度会减小,其中通行能力范围内的车流以Vm=0.5V0的速度通过,而剩余的车辆要排队通过,直至排队消散[17].

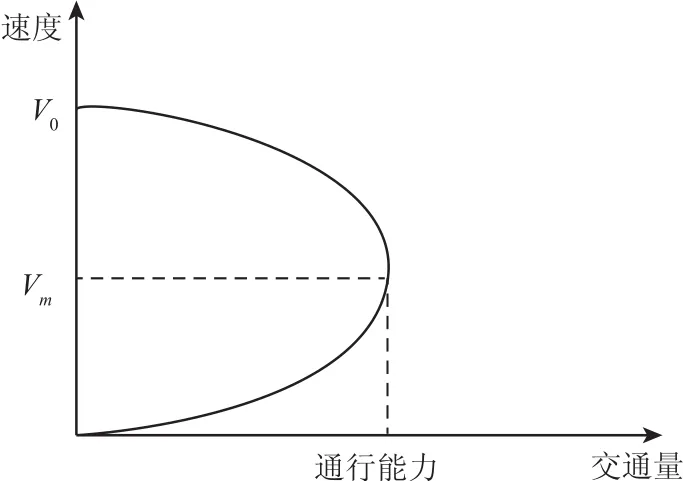
图1 车速-流量模型曲线Fig.1 Speed-flow model curve

当单位时间t内到达的流量q超过通行能力c时,排队长度为q-c.假设t时段以后到达的车辆在排队车辆之后等待通行,在排队过程中不发生因车流不稳定而造成的阻塞,则在整个排队消散的过程中,路段上的交通流以Vm通过,可以得到

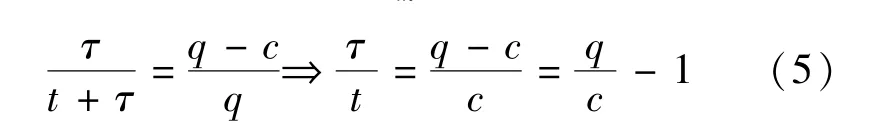
直接用式(5)求解速度往往偏大,例如当q/c =2时有τ=t,即V=V0/2=Vm,明显偏大.我们知道,在排队消散的过程中车流不可能以Vm匀速通过.实际上,当流量超过通行能力时,车流已经不稳定,任何交通条件的影响都会引起更大的延误,甚至阻塞.因此需要引进参数α,β进行修正

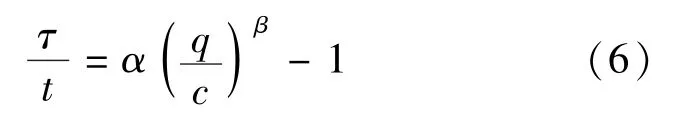
在时段t内到达车流通过路段的平均延迟时间为

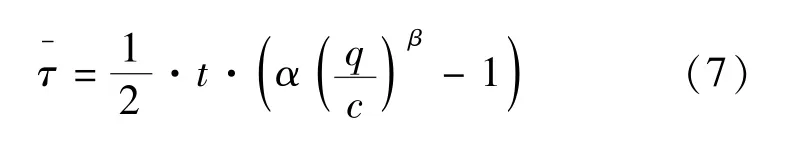
定理2 设(Vi,qi)是交通系统中测得的速度-流量序列,对其建立如下速度-流量模型

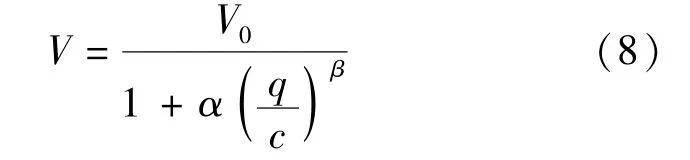
参数α,β为

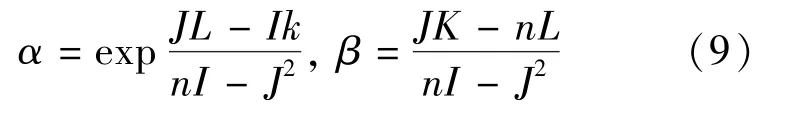
式中

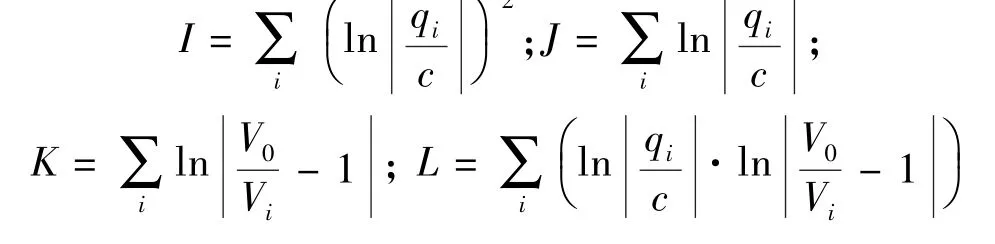
证明 路段的实际行驶距离l=Vm·t,则t+τ-时间内到达车流的平均速度为

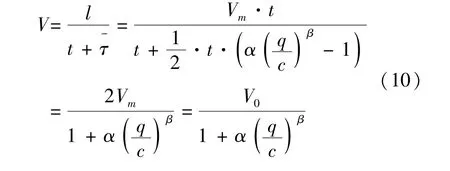
得到速度-流量模型.将式(8)变形并两边取对数可以得到

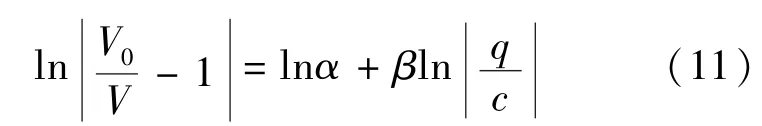
将(Vi,qi)序列代入式(11),得到方程组

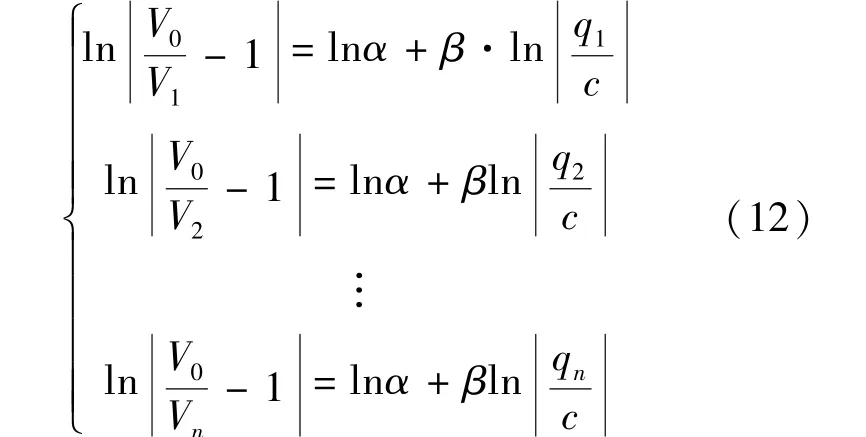
令

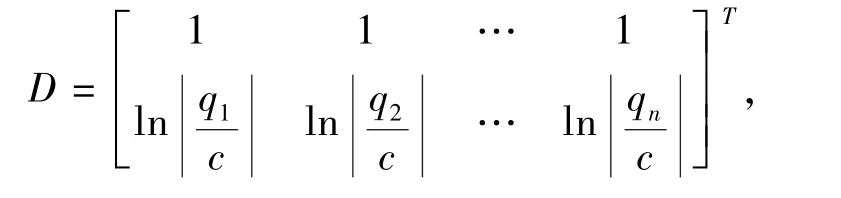
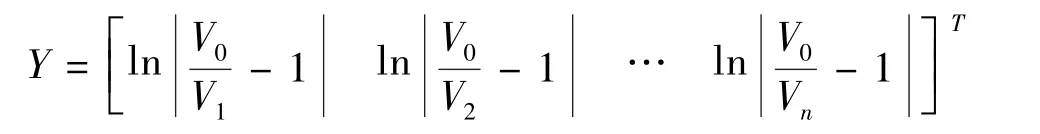
由最小二乘法得到

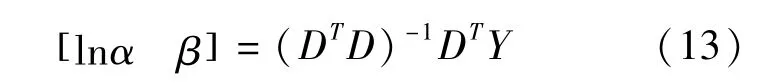
进行矩阵运算,令

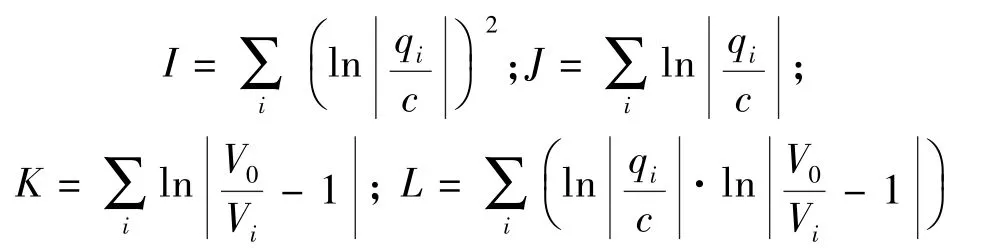
得到

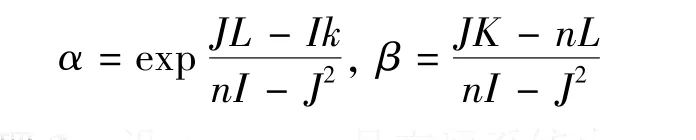
定理3 设(Vi,qi)是交通系统中测得的速度-流量序列,则所测时间段内系统的延迟时间为τ,且

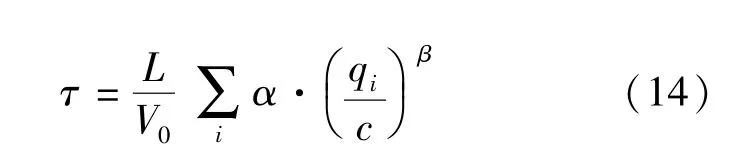
式中 α,β如定理2；L为所测路段长度；V0为自由流车速.

证明 交通系统中车流在不考虑延迟的情况下,通过长为L的路段需要的时间为然而作为一个整体的交通系统,流量为qi时车流的实际通行时间为T(qi),根据定理2,可以得到

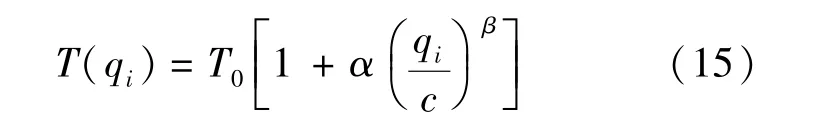
式中 α,β如定理2所得.那么该时段的延迟时间为τ(qi),且

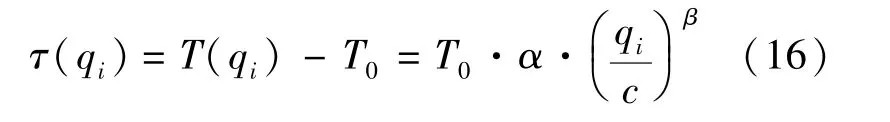
则所测时间段内交通流系统的延迟时间τ,且

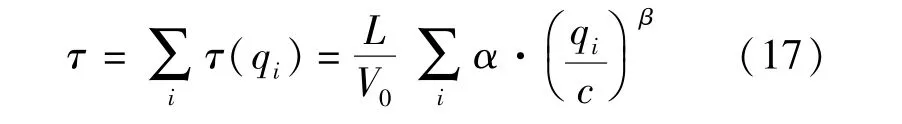
2.3 非线性因子的确定

为检验模型模拟和预测的效果,我们定义预测误差指数指标——平均相对误差(MRE)和拟合度(FD fitting degree)(预测值与真实值之间),计算公式为

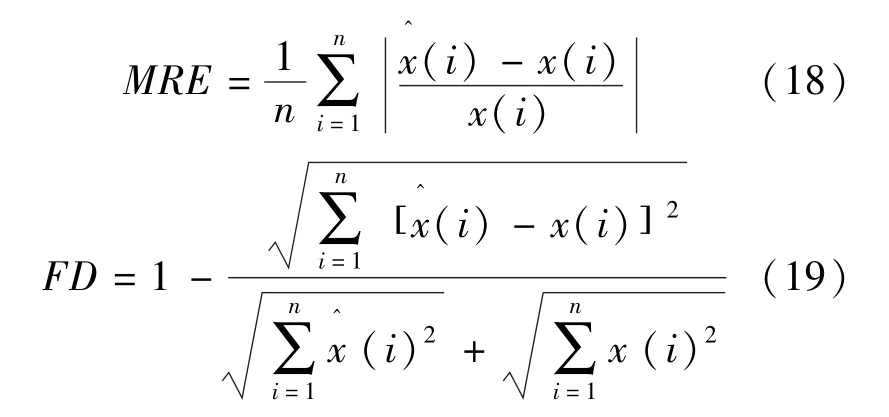
MRE和FD值的大小充分反映了预测效果的好坏,MRE的值越小,说明拟合和预测精度越高；对于FD,凡FD＞0.85的预测都视为较好的预测,凡FD＞0.95的预测都视为满意的预测.FD值越高,整体预测效果与实测值越接近,效果也接近理想.因此,在延迟因子τ确定的情况下,我们构造寻找最佳非线性因子r的优化模型:

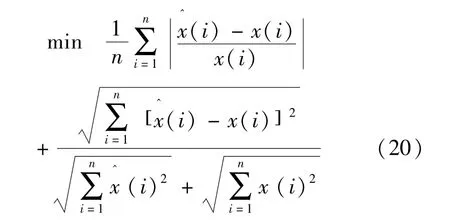
这里采用粒子群算法(PSO)来求解非线性因子r.

3 实例分析

为解决交通系统中的实际问题,我们于2010年5月19日15:00-17:00在武汉市武昌区友谊大道园林路和建设一路路段上采用摄像机跟拍进行实验.所测路段长度L=949 m,查阅城市车道通行能力数值表[17],所测路段的通行能力C=1 600辆/h、设计速度V0=60 km/h,则实验所采用5分钟一个时间间隔的通行能力c=134辆,不考虑系统延误的运行时间T0=L/V0=56.94 s.取5 min为一个时间间隔,利用SAVA视频分析软件处理实验采集的视频信息,得到交通流量(辆)和采集点的地点车速(km/h),如表1所示.

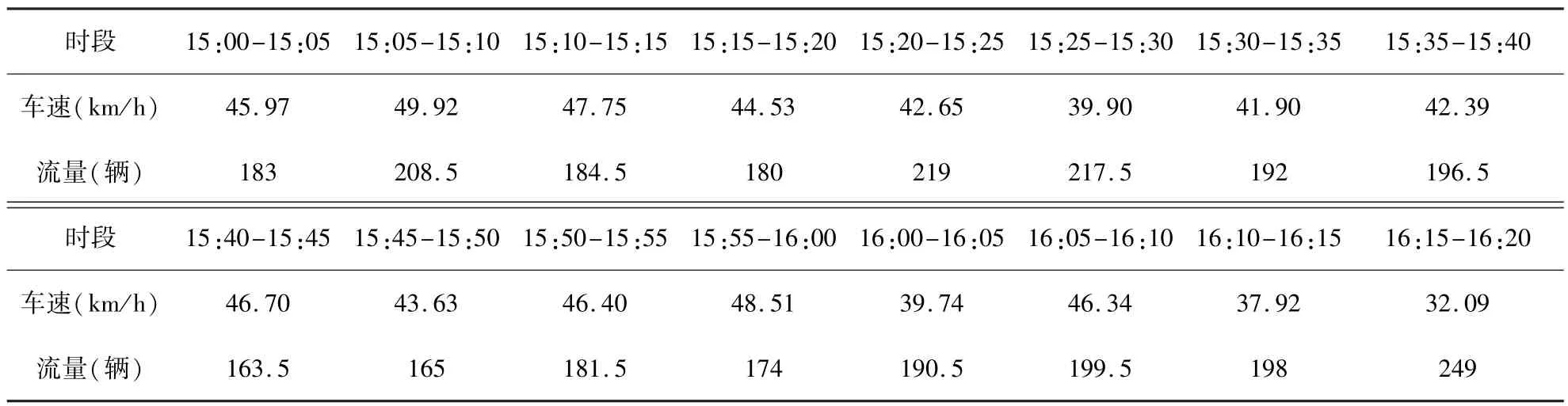
表1 实测交通流量Table 1 Measured traffic flow

利用流量和速度数据(表1),根据定理2得到α=0.161 227,β=3.092 102.由式(16)、式(17)得到整个交通系统的延迟时间τ=705 s,即系统的延迟时间为11.75 min.在实验中我们采用5 min为一个时间间隔,延迟时间接近两个时间间隔,因此延迟因子τ=2,可以建立GM(1,1|τ,r)模型如下:

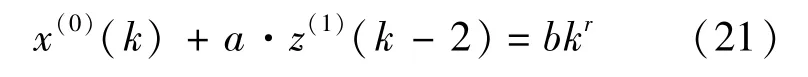
由于交通流量数值比较大,在求解参数向量P =[a b]T时可能会存在矩阵求逆奇异的问题,我们对原始数据进行数乘变换来避免此类问题发生.根据定理1,数乘变换不改变原始数据的趋势.运用所测的前10个数据进行建模,根据粒子群寻优算法得到r=0.948 5,进而得到a=0.389 3,b= 84.504 0,于是GM(1,1|τ,r)模型为

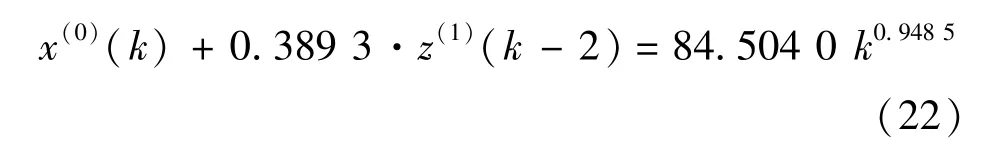
根据模型(22)对原始数据进行拟合,并与支持向量机和GM(1,1)模型的拟合结果进行比较,如表2所示.

由表2可知,支持向量机拟合的平均相对误差为5.295 76%,拟合度为0.967 589；GM(1,1)模型拟合值的平均相对误差为6.854 273%,拟合度为0.959 862；GM(1,1|τ,r)模型拟合值的平均相对误差为5.027 57%,拟合度为0.968 109.将拟合结果在图2中进行比较,显然GM(1,1|τ,r)模型的拟合效果优于GM(1,1)模型和支持向量机的拟合效果.

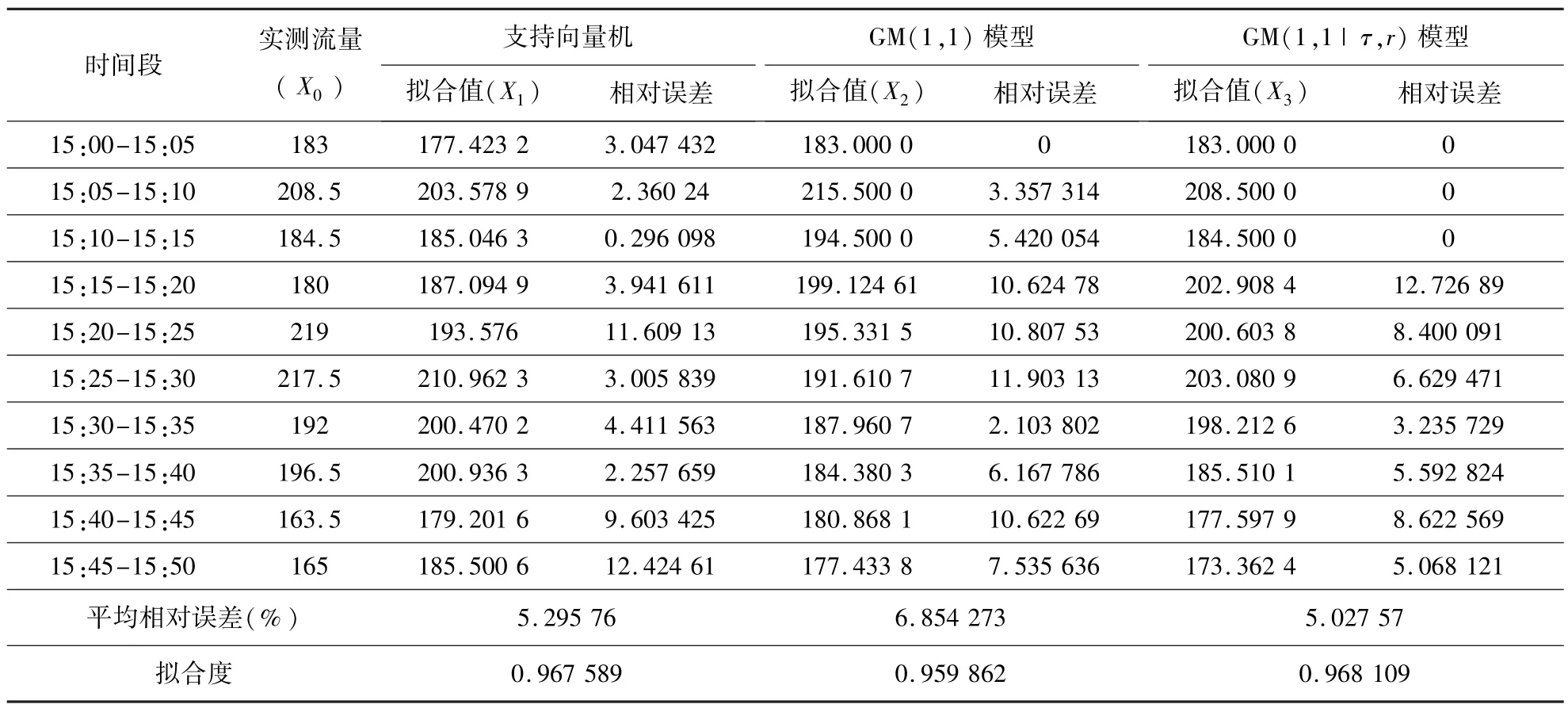
表2 拟合结果比较Table 2 The comparing of fitting results

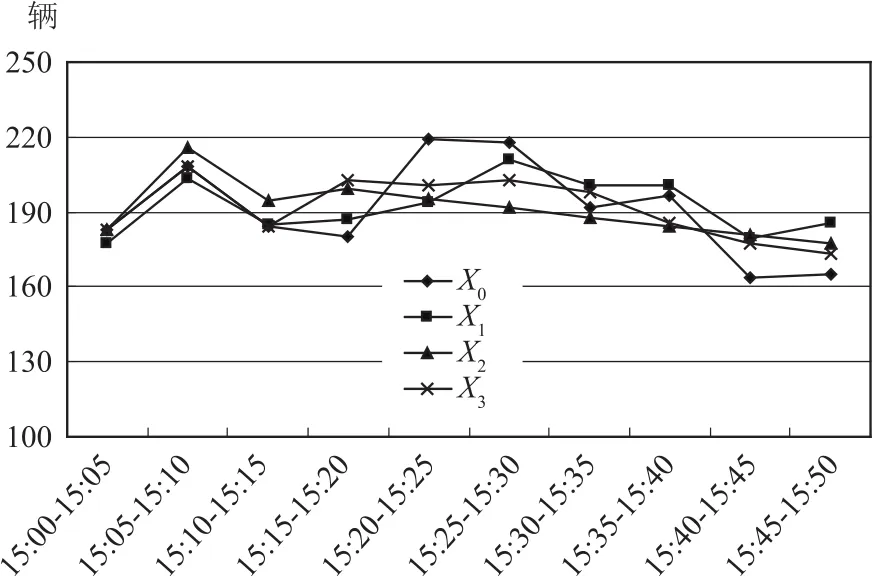
图2 实测流量与模型拟合值Fig.2 Measured flow and fitting value of model

根据模型(22)对接下来时刻的交通流进行预测,并将预测结果进行比较,如表3所示.由表3可知,支持向量机预测的平均相对误差为10.538 55%,拟合度为0.940 827(＜0.95)；GM(1,1)模型预测值的平均相对误差为15.14%,拟合度为0.880 682(＜0.9)；GM(1,1|τ,r)模型预测值的平均相对误差为6.450 623%,拟合度为0.958 437(＞0.95).将预测结果在图3中进行比较,GM(1,1|τ,r)模型的预测值接近实测值.这说明,GM(1,1|τ,r)用于交通流的预测,考虑了交通系统存在的延迟性和非线性,真实地反映了交通系统状况,可以得到满意的预测结果,可以用于智能交通的管理.

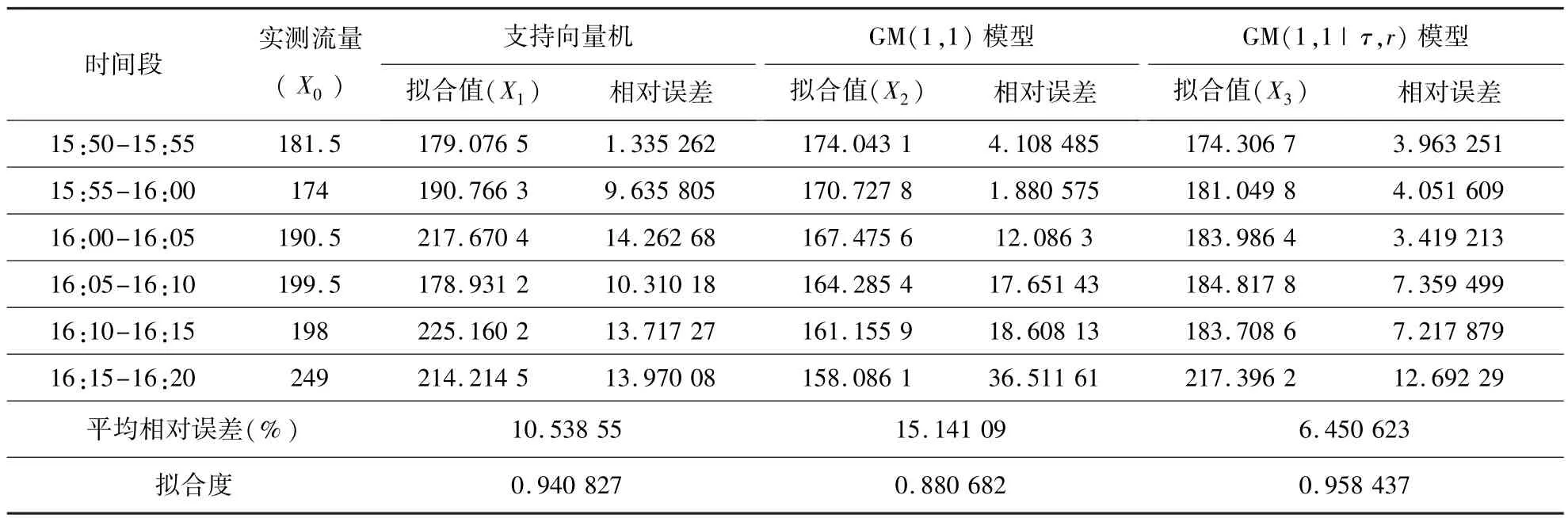
表3 预测结果比较Table 3 The comparing of forecast results

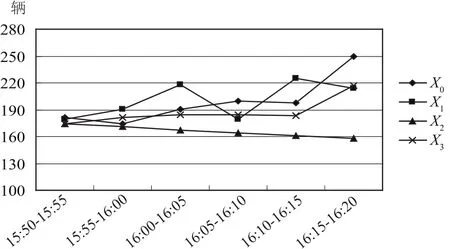
图3 实测流量与模型预测值Fig.3 Measured flow and forecasting value of model

4 研究结论

为缓解城市交通问题,优化智能交通系统,需要精确可靠的短时交通流预测.充分考虑道路交通流的延迟性和非线性,本文基于灰理论提出一种短时交通流的预测方法.由于交通流的延迟性,利用交通理论中三参数的关系推导延迟时间τ的计算模型.再针对交通流的非线性特征,以模型的预测效果最佳为目标,建立优化模型并利用粒子群算法寻找最佳的非线性参数r.最后对武汉市武昌区友谊大道园林路和建设一路路段进行实验,分析路段的实际状况并根据实测数据建立GM(1,1|τ,r)模型进行拟合和预测,将结果与未考虑延迟性和非线性的GM(1,1)模型和支持向量机算法做比较, GM(1,1|τ,r)模型表现出明显的优势.本文的研究可在一定程度上推广短时交通流的预测方法,为智能交通系统提供有效的信息,达到解决交通系统实际问题的目的.然而交通流数据实际存在波动性,此后还有必要对存在波动性的交通流系统进行建模研究.

[1] Willam R.Mcshane,Roger P Roess.Traffic engineering [M].N.J.:Prentice-Hall,1990.

[2] Queen C M,Albers C J.Intervention and causality: forecasting traffic flows using a dynamic Bayesian network[J].Journal of the American Statistical Association,2009,104(486):669-681.

[3] Ghosh B,Basu B,O'Mahony M.Bayesian time-series model for short-term traffic flow forecasting[J]. Journal of Transportation Engineering-asce,2007,133 (3):180-189.

[4] Xie Y C,Zhao K G,et al.Gaussian processes for short-termtrafficvolumeforecasting[J]. Transportation Research Record,2010,2165:69-78.

[5] Xue J N,Shi Z K.Short-time traffic flow prediction based on chaos time series theory[J].Journal of Transportation Systems Engineering and Information Technology,2008,8(5):68-72.

[6] 杨兆升,王媛,管青.基于支持向量机方法的短时交通流量预测方法[J].吉林大学学报(工学版), 2006,36(6):881-884.[YANG Z S,WANG Y, GUAN Q.Short-term traffic flow prediction method based on SVM[J].Journal of Jilin University (Engineering and Technology Edition),2006,36 (6):881-884.]

[7] Huang S,Sadek AW.A novel forecasting approach inspired by human memory:The example of shortterm traffic volume forecasting[J].Transportation Research Part C-Merging Technologies,2009,17 (5):510-525.

[8] 邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002.[DENG J L.Grey theory foundation[M]. Wuhan:HuazhongUniversityofTechnology Press,2002.]

[9] 邓聚龙.灰预测与灰决策[M].武汉:华中科技大学出版社,2002.[DENG J L.Grey prediction and decision[M].Wuhan:HuazhongUniversityof Technology Press,2002.]

[10] Deng J L.A novel grey model GM(1,1|τ,r): generalizing GM(1,1)[J].The Journal of Grey System,2001,13(1):1-8.

[11] Deng J L.Solution of grey differential equation for GM(1,1|τ,r)in matrix train[J].The Journal of Grey System,2002,14(1):105-110.

[12] Deng J L.On boundary of parameters in GM(1,1|τ, r)[J].The Journal of Grey System,2001,13(2): 199-200.

[13] Jiang X,Wang B W,Chen F X.Based GM(1,1|τ, r)-moving object segmentation[J].The Journal of Grey System,2003,15(2):101-106.

[14] W C Huang,M S Kuo,et al.Application of GM(1,1 |τ,r)to analyze the ports for putting in resources [J].The Journal of Grey System,2004,16(6): 211-220.

[15] Guo H,Xiao X P.Intelligent traffic signal dynamic optimization design based on grey theory[J].Journal of Grey System,2012,(2):107-118.

[16] 肖新平,宋中民,李峰.灰技术基础及其应用[M].北京:科学出版社,2005.(XIAO X P,SONG Z M, LI F.Grey technical foundation and its application [M].Beijing:Science Press,2005.)

[17] 戴冀峰,马健霄.交通工程概论[M].北京:人民交通出版社,2006.[DAI J F,MA J X.Traffic engineeringconspectus[M].Beijing:China Communications Press,2006.]

Urban Road Short-term Traffic Flow Forecasting Based on the Delay and Nonlinear Grey Model

GUO Huan1,XIAO Xin-ping1,Jeffrey Forrest2
(1.School of Science,Wuhan University of Technology,Wuhan 430063,China；2.Mathematics Department,Slippery Rock University,PA 16057,USA)

Concerning the delay and nonlinear properties of traffic flow in urban road systems,this paper forecasts the short-term traffic flow based on the grey model.Firstly,the delay factor is determined by the speed-flow relationship when volume is greater than it capacity.Then,the nonlinear parameter is determined by a particle swarm optimization algorithm,where the prediction effect is unsurpassed.Finally,verification of this model is done by collecting traffic flow data on one section of Youyi Avenue and comparing the prediction value of with and SVM.The results show that the prediction effect of model for short-term traffic flow is significantly improved,which plays an important role in intelligent traffic systems.

urban traffic；GM(1,1|τ,r)model；short-term traffic flow forecasting；speed-flow model；delay time；nonlinear

U491.1+4

A

U491.1+4

A

1009-6744(2013)06-0060-07

2013-02-06

2013-07-30录用日期:2013-08-14

国家自然科学基金(70971103)；教育部人文社科基金(11YJC630155)；教育部高等学校博士学科专项科研基金(20120143110001)；武汉理工大学国际交流预研项目(2012-JL-06).

郭欢(1984-),女,湖北襄阳人,博士生.

*通讯作者:xiaoxp@263.net