多重共线性的解决：剔除变量的新标准

刘 明

（兰州商学院a.甘肃经济发展数量分析研究中心；b.统计学院，甘肃兰州 730020）

0 引言

线性回归模型的多重共线性的本质是解释变量之间存在线性相关。多重共线性的解决有多种经验性方法，这些方法因模型和样本数据的不同而各异，其中一类比较常用而且简单的办法是“剔除变量法”，即剔除引起多重共线性的解释变量，以达到解决多重共线性问题的目的。实施剔除变量法的关键是确定哪一个或哪些变量应该被剔除，因此需要确立剔除依据。文献[1,2]认为可以根据方差膨胀因子（VIF）的大小来选择被剔除变量，VIF最大的变量应首先剔除。该依据的理由是，VIF最大的变量与其余变量的相关性最强，因而是多重共线性的罪魁祸首，因此应首先剔除。为考察这种方法的效果，首先看一个实例，这也是研究的出发点。

1 剔除变量法的一个实例：以方差膨胀因子为准则

为展示以方差膨胀因子为准则的剔除变量的方法，这里利用朗利数据构造一个例子。数据如下表，其中Y=被雇佣人数（千人），X1=GNP价格缩减指数，X2=GNP（百万美元），X3=失业人数（千人），X4=服役人数（千人），X5=14岁以上非编制人口，X6=时间。原数据参见文献[3]。

表1 朗利数据

利用上述数据，以Y为被解释变量，其余变量为解释变量构建线性回归模型如下：思想，选择方差膨胀因子最大的解释变量予以首先剔除。解释变量的方差膨胀因子计算结果依次为：

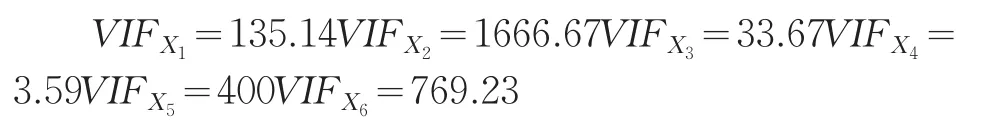
显然，X2的方差膨胀因子最大，先将其剔除。剔除后重新构建的回归模型为：

其中括号内为t检验统计值，为节约篇幅，其余统计量均未给出。此模型整体拟合效果较好，可决系数R2=0.9955接近于1，但部分解释变量不显著，因而可能存在多重共线性问题，经过进一步诊断，模型确实受到共线性问题干扰。考虑使用剔除变量法解决多重共线性问题，依据该方法的

经检验，该模型仍存在多重共线性问题，继续实施剔除变量法，选择该模型中方差膨胀因子最大的解释变量予以剔除，剔除后继续构建回归模型并检验是否存在多重共线性问题，若存在，继续按上述过程剔除变量，直到无多重共线性问题存在为此。最终得到的模型是：

该模型的可决系数R2=0.5608，相对偏小，而且模型中仅剩余两个解释变量X3、X4，因此该模型没有达到对原问题的正确表述。

2 选择被剔除变量的新标准：t统计量

上述例证说明，以方差膨胀因子为标准实施的剔除变量法不能够很好的解决多重共线性问题，甚至不能解决多重共线性问题。究其原因，方差膨胀因子仅考虑了解释变量间的相互关系，尽管这种关系对于模型是否存在多重共线性问题来说也很重要，但没有考虑解释变量与被解释变量之间的关系，即不同的解释变量对被解释变量的影响作用是不同的。因此，仅考虑解释变量之间的关系来解决多重共线性问题是不全面的。方差膨胀因子就是一类仅考虑解释变量关系的统计指标，因而不能作为解决多重共线性问题中选择被剔除变量的标准。

t统计量可以作为选择被剔除变量的标准。其理由有二：一是t统计量的构造既包含了解释变量之间相关性的信息——估计量的标准差的估计量中含有方差膨胀因子，如前所述，这是反映解释变量间相关性的统计指标，同时也包含了解释变量对被解释变量的影响关系——参数估计量即表述了解释变量对被解释变量的影响；二是t统计量的取值反映了所对应的解释变量对被解释变量影响贡献程度的大小[4]，在同一模型的所有解释变量中，t统计量绝对值越小，该解释变量对被解释变量的影响作用就越小，相反，t统计量绝对值越大，影响作用就越大。因此，选择t统计量作为剔除标量的标准是全面的，可靠的。

利用t统计量作为选择被剔除变量的标准，其具体做法是，最先剔除对被解释变量贡献最小的解释变量，即t统计量绝对值最小的解释变量，利用剩余变量重新构造回归模型，若仍存在共线性问题，则重复前一过程，直到无多重共线性问题为止。下面即利用该方法来解决上述例子中的多重共线性问题。

首先将所有解释变量纳入到模型中构建回归模型，如前文中所建的第一个模型。选择首先被剔除的解释变量，依据是未通过t检验的t统计量绝对值最小。当然，若所有的t检验均通过，则不需要剔除变量了。显然，X1首先被剔除。重新构建的回归模型如下：

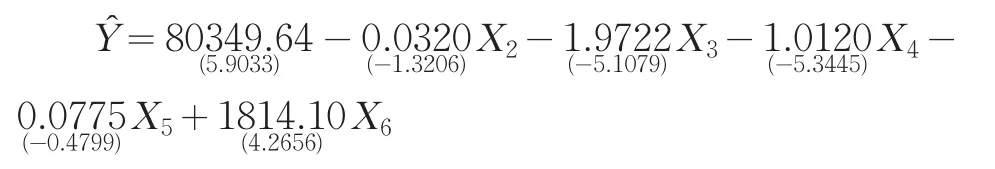
不难发现，该模型仍受到多重共线性的干扰，继续使用剔除变量法，根据t统计量的绝对值大小选择X5被剔除。剔除后构建的回归模型为：

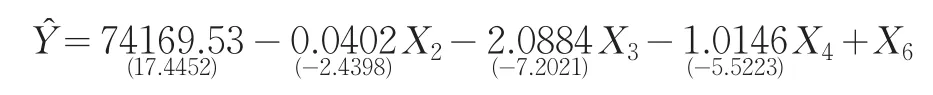
通过检验发现，此模型不再受到多重共线性的干扰，各解释变量均显著，整体拟合效果较好，其可决系数R2=0.9954，因而此模型解决了多重共线性问题，是排除多重共线性后的最优模型。

根据上述例证，将以方差膨胀因子为准则的多重共线性解决方法和以t统计量绝对值为准则的方法相比较，不难发现，前者所构建的回归模型结果不够理想，主要表现为删除的解释变量过多、模型整体拟合效果较差、计算步骤繁琐等。而后者得到了一个包含尽可能多解释变量的模型，大大降低了存在设定误差的可能性，同时模型的拟合效果更好，计算更简便。因此，以t统计量绝对值为准则剔除变量的多重共线性解决办法更优。

3 结论

简单地说，以t统计量为准则剔除变量的多重共线性解决办法就是剔除模型中不显著的解释变量，是否剔除的判断依据就是该变量显著性t检验统计量绝对值的大小。当然，这不是说将所有未通过t检验的解释变量全部剔除——这样做可能会将一些显著的解释变量排在模型之外，而是逐一的剔除，直到多重共线性问题得到解决为止。选择t统计量作为被剔除变量选择的标准，是因为它不仅含有解释变量间相关性的内容，还反映了解释变量对被解释变量的影响作用，信息涵盖更全面。由于t统计量在一般计算机软件计算中都会给出，因而这种解决办法更方便快捷。

[1]李占风.经济计量学[M].北京:中国统计出版社,2010.

[2]庞皓.计量经济学（第2版）[M].北京:科学出版社,2010.

[3]古扎拉蒂.计量经济学基础（第4版）[M].北京:中国人民大学出版社,2005.

[4]刘明,王仁曾.基于t检验的逐步回归的改进[J].统计与决策,2012,(6).