MTPT方法估计机载SAR残余运动的两个影响因素
钟雪莲* 陈仁元 杨 然 吴 涛
MTPT方法估计机载SAR残余运动的两个影响因素
钟雪莲陈仁元 杨 然 吴 涛
(中国电子科技集团第三十八研究所合肥 230088)
由于导航系统测量精度的限制,载机的位置经常存在厘米级的误差,该误差称为残余运动误差。对于机载超高分辨SAR系统或机载重轨干涉SAR,必须估计并补偿该残余运动误差。MTPT方法可以估计单幅SAR图像中的残余运动误差,但是速度和斜距的误差会影响该方法的精度。该文在详细分析速度和斜距误差对MTPT方法进行残余运动估计的影响的基础上,利用仿真和实测SAR数据验证了这一点。同时还指出,MTPT方法虽然可以估计速度和斜距误差,但是它们的精度敏感于相位测量误差;在利用MTPT方法进行估计之前必须先利用其它更为准确的方法消除平台的速度误差和目标的斜距误差。
机载SAR;残余运动;速度误差;斜距误差
1 引言
机载合成孔径雷达(Synthetic Aperture Radar, SAR)在获取回波数据时,由于大气气流的影响,载机平台会偏离参考轨迹几米、几十米。通过GPS/INS(Global Positioning System/Inertial Navigation System)组合导航系统测量载机的位置,在SAR成像的时候进行两级运动补偿,可以得到聚焦很好的幅度图像,能够满足一般目标判别的要求。在对相位要求很高的应用中,还需要补偿由于平地和中心假设引起的相位误差。但是,即使使用DGPS (Differential Global Positioning System)进行导航数据的后处理之后,目前的导航系统仍只能达到2-10 cm的定位精度。该定位误差是无法通过仪器测量的方法消除的,而未补偿的误差会在SAR图像中产生散焦和相位误差。我们将导航系统定位精度的限制而引起的这部分误差称为残余运动误差。对于超高分辨SAR成像系统或干涉、差分干涉等应用,必须考虑残余运动误差的影响。
在文献[10-12]中,作者提出了一种估计单幅SAR图像中的残余运动误差的方法MTPT(Multi-squint Technique with Point Targets)。该方法通过沿方位向分布的一系列点目标,利用子孔径的方法测量相邻子孔径间的相位差,得到残余运动误差的2阶导数,然后通过两次积分得到最终的残余运动误差。通过仿真和实测数据,MTPT方法的有效性得到了验证。但是,该方法能够正确运用的前提是假设成像过程中的参数是准确的,除了残余运动误差,不存在其它的误差源使得两子孔径间存在相位差。但在实际成像过程中,载机平台的速度并没有达到惯导系统所标称的测量精度,而是存在相当大的测量误差。同时,很多机载试验都缺乏精确的外定标过程,用于标定天线相位中心与场景目标间准确的斜距,尤其需要考虑雷达系统延时的影响。而速度和斜距的误差将会导致图像方位压缩的恶化。这种影响同样反映在相邻子孔径间的相位差上,从而影响真正意义上的残余运动的估计。本文我们将重点分析速度和斜距的误差对残余运动估计的影响,并提出相应的解决办法。
2 MTPT方法
我们首先简单介绍MTPT方法。对于一个点目标,在存在残余运动时,目标的峰值位置和相位会发生变化。而在较短的时间内,残余运动可以近似认为是线性的。我们发现,残余运动的斜率与目标相对于理想位置的方位向偏移量有关,而它的峰值相位与残余运动在该点的理想方位位置处的截距有关。对于两相邻子孔径图像,如果两者的残余运动相同,包括截距和斜率,那么对于该点目标,它在两子孔径中的位置和相位都相同。如果两子孔径包含的残余运动不同,那么该点目标在两子孔径图像中的位置和(或)相位也是不同的,而位置的不同也可以换算为相位的差异。如图1所示,通过测量两子孔径中目标相位的差异可以得到残余运动的2阶导数:
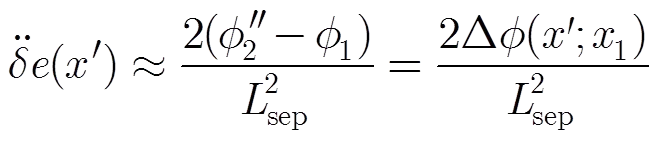
(2)

图1 残余运动引起子孔径图像中目标的位置和相位的变化示意图
3 速度和斜距误差的影响
对于SAR回波信号,在斜视角为零且孔径不大的情况下,方位向调频率可近似为

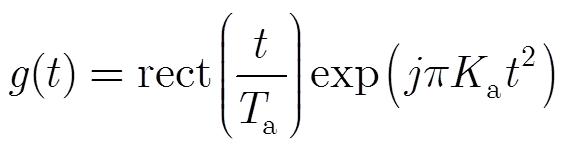
(5)
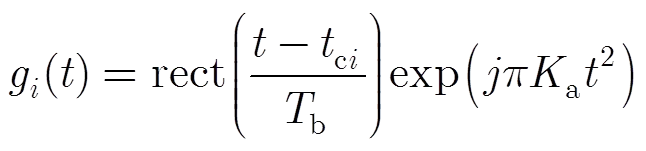
则匹配滤波输出为
因为匹配滤波器的矩形窗比子孔径的方位向信号长,因此,可以去除该矩形窗。对式(7)进行变量替换,并化简得

式(8)积分号中的第1个指数项为调频率误差造成的2次相位,它引起的最大2次相位误差(Quadratic Phase Error, QPE)为
(9)
由于该相位误差是2次的,它不会改变目标压缩的位置,但会在目标峰值位置处引入绝对相位误差,其大小约为QPE的。因此,式(8)积分号中的信号被压缩到时刻处。在该位置处,式(8)中第1, 2指数项的相位和为

(11)
对于该孔径,压缩后的目标位置与理想目标位置间的偏移量为

同理可得,第+1个子孔径图像中点目标的位置和相位的变化量分别为
(13)

由于两子孔径的方位调频率误差和孔径长度相等,因此,它们的QPE相等。
假设第,+1个子孔径图像中目标峰值处的相位分别为和,若点目标在两子孔径图像中的理想相位为,则有

(16)
根据MTPT的计算方法,需要考虑在第1个子孔径图像的目标峰值位置处,两相邻子孔径图像的相位差。因此,在第个子孔径图像的目标峰值位置处,第+1个子孔径图像的相位为

(18)
由于全孔径的多普勒中心为零,因此,按照误差调频率计算可以得到第+1个子孔径的中心为
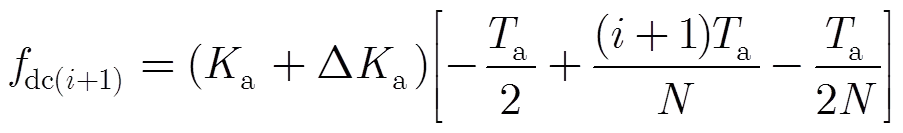
(20)
由式(20)可知,方位向调频率存在误差必然会引起两相邻子孔径间相位差的变化,且该变化量的大小只与方位向调频率误差以及子孔径的个数有关。因此,在进行残余运动估计时,如果不考虑方位向的调频率误差必然会导致残余运动的过度估计。
如果只存在速度误差,那么可利用式(3)和式(20)计算实际的平台运动速度

同理,若只有最近斜距存在误差,也可以利用式(3)和式(20)计算实际的斜距为
(22)
4 试验结果
这部分主要利用仿真和实测数据来验证上述结论。仿真的参数如表1所示。在场景中心距离处、沿方位向分布了120个点目标,它们的间隔为10 m,见图2。为了更好地观察速度和最近斜距误差造成的影响,场景中没有加入背景噪声的影响。数据获取的斜视角为零。整个合成孔径分成3个不重叠的子孔径,每两相邻子孔径都可以计算这些点目标的相位差。而且,理论上,在相同的子孔径长度的条件下任何相邻的子孔径的相位差都是相等的。为了获得可靠的结果,将这些测量的相位值进行平均。图3(a)显示了速度误差为0.25 m/s时(即此时的成像速度为100.25 m/s),测量的两相邻子孔径的平均相位差。这里将离散的数值进行了插值使得它在方位向连续。测量得到的平均相位差约为,代入式(21)计算的实际速度约为100.01 m/s。如果利用此相位差根据MTPT方法反演残余运动误差,将会得到方位向2次相位误差,如图3(b)所示。MTPT方法通过补偿该相位误差,达到提高方位压缩质量的目的。
表1仿真的系统参数

Tab. 1 System parameters for simulation

图2 仿真数据获取的几何示意图

图3 速度存在0.25 m/s的误差时,测得的相邻子孔径的相位差和利用MTPT方法计算得到的方位向2次相位误差
图4(a)显示了最近距误差为50 m时(即此时所用的成像斜距为9050 m),测得的相邻子孔径的平均相位差。由于该相位差对相同距离处的所有目标都是相同的,因此,可以将所有方位上测得的相位差再进行平均,得到最终的相位差为。将该值代入式(22)中,计算可得斜距的误差为48.7 m。根据该相位差反演得到的方位向2次相位误差见图4(b)。
利用实际数据进行MTPT处理时,我们也同样发现了沿方位向分布的2次相位误差。图5是利用实际的X波段数据通过MTPT方法估计的水平和垂直方位的相位误差。从图中可以看出,沿着方位向存在非常大的2次误差,该误差很可能是由速度误差或斜距误差引起的。由于该误差非常大,真正的残余运动误差反而观察不到了。补偿完该误差后,点目标的压缩有很大的提高,见图6。虽然利用MTPT方法,也可以估计和补偿由速度和斜距误差引起的误差相位,但由于MTPT方法主要考虑垂直航向上的平台位置误差,其数学模型与由速度和斜距引起的误差的数学模型是不同的。因此,MTPT并不能完全准确地估计出每个距离位置上的误差相位,会导致某些距离上的估计误差非常大。对于实测的机载X波段双天线SAR数据,利用MTPT方法分别估计主、辅图像中的残余运动误差后,在不同的距离处比较两者的估计结果,见图7。由于双天线SAR系统的两个天线是刚性连接的,因此,两者的残余运动误差应该基本一致。但图7显示的估计结果表明,不同距离处两者的残余运动误差不同,且近距处的误差最大。以前,我们总将这个现象归因于该距离位置上点目标样本数不多的缘故,但现在看来,其根本的原因还是在于速度和斜距误差引起的数学模型失效所致。
还有一个问题需要解释的是,从式(21)和式(22)可以反演速度和斜距误差,那么是否就可以利用该方法先将这两个误差估计出来,然后再利用MTPT进行残余运动估计呢?要回答这个问题,还需要考虑该方法进行估计的敏感度。将式(21)的两端分别对速度和相位差求微分,可得
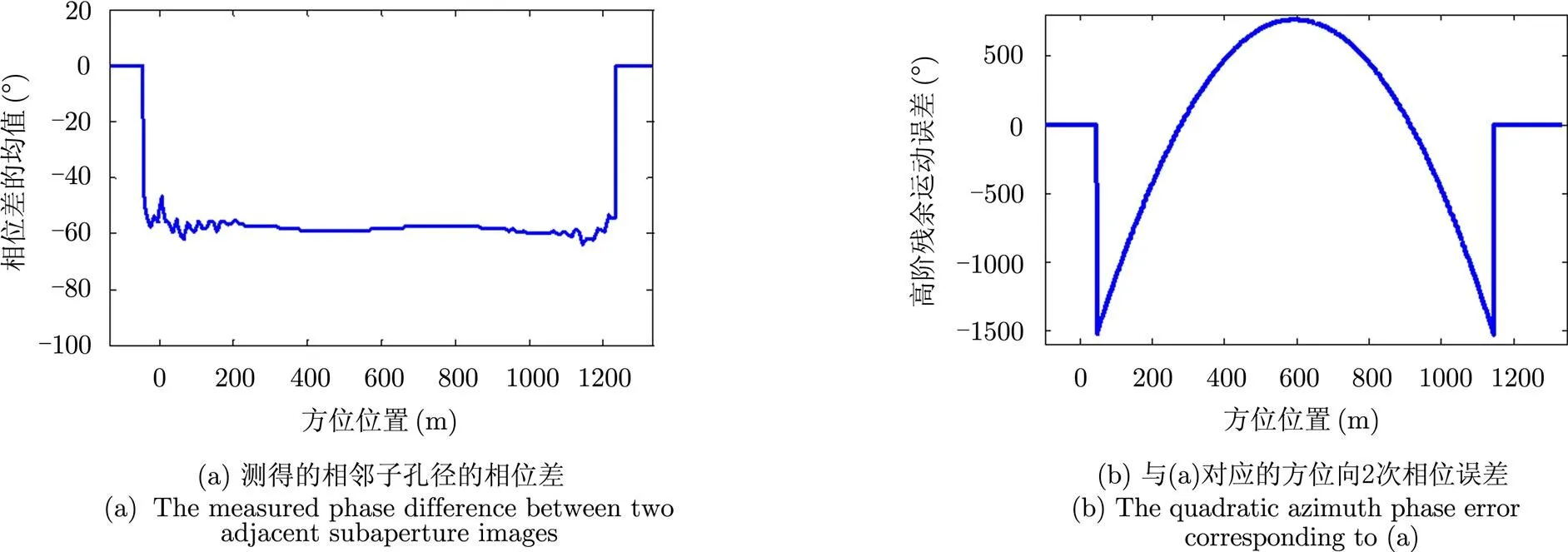
图4 斜距误差为50 m时,测得的相邻子孔径的相位差和利用MTPT方法计算得到的方位向2次相位误差
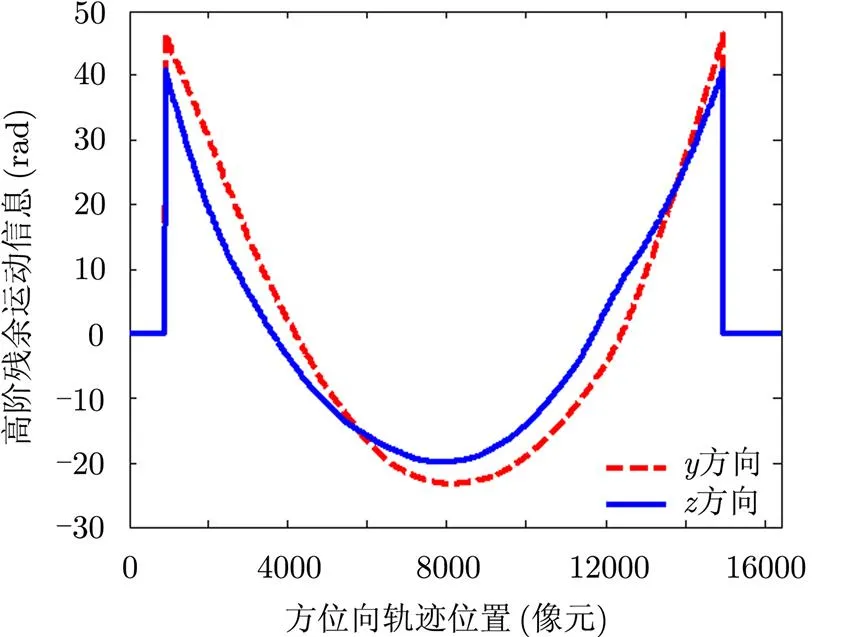
图5 从实际的X波段SAR图像中利用MTPT估计得到的相位误差

图6 在补偿图5所示的相位误差前后,点目标方位向脉冲响应的比较,64倍升采样

图7 对于X波段双天线SAR数据,MTPT方法估计的主、辅图像的残余运动在不同距离处的差异
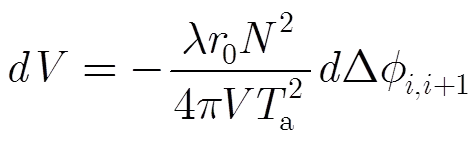
(24)
那么,对于表1中的仿真参数,测量的相位误差与速度估计误差的关系见图8(a)。从图中可以看到,的相位测量误差将会引起-0.0046 m/s的速度估计误差,这与惯性导航系统所能达到的速度测量精度相当。而在实际情况中,由于背景噪声的影响,相位测量很难达到如此高的准确度。对于斜距误差,同样存在这个问题,的相位测量误差将会引起0.83 m的斜距估计误差,见图8(b)。而且,速度和斜距在整个成像过程中都需要使用,不仅仅在方位压缩的时候。因此,如果利用该方法估计速度和斜距误差,必然需要重新进行成像处理。这样看来,利用这种方法估计速度和斜距误差的精度和计算效率都并不高。所幸的是,有很多方法可以在成像过程中就可以估计平台的速度,而通过外定标可以准确获得目标的斜距,消除雷达内部延迟的影响。

图8 相位测量误差对速度和斜距估计的影响
5 结束语
本文详细分析了MTPT方法进行残余运动估计时,平台速度误差和目标的最近斜距误差对MTPT方法的影响。指出,速度和斜距存在误差时,将会在MTPT方法进行残余运动估计时引入沿方位向的2次相位误差,从而造成残余运动的过度估计。利用仿真和实测的数据,这一点得到了验证。同时指出,虽然可以通过MTPT方法估计速度和斜距误差,但两者对测量相位的误差非常敏感,在对测量精度要求很高的场合,该方法并不适用。为了获得准确的残余运动估计,必须先通过高精度的速度和斜距估计方法消除这两者的误差,然后再利用MTPT方法进行残余运动的估计。
[1] Moreira A and Huang Y. Airborne SAR processing of highly squinted data using a chip scaling approach with integrated motion compensation[J]., 1994, 32(5): 1029-1040.
[2] Reigber A, Alivizatos A, Potsis A,.. Extended wavenumber-domain Synthetic Aperture Radar focusing with integrated motion compensation[J].-,, 2006, 153(3): 301-310.
[3] Macedo K and Scheiber R. Precise Topography-and Aperture-Dependent motion compensation for airborne SAR[J]., 2005, 2(2): 172-176.
[4] Prats P, Reigber A and Mallorqui J. Topography-dependent motion compensation for repeat-pass interferometric SAR systems[J]., 2005, 2(2): 206-210.
[5] Cantalloube H and Dubois-Fernandez P. Airborne X-band SAR imaging with 10 cm resolution: technical challenge and preliminary results[J].-,, 2006, 153(2): 163-176.
[6] Prats P, Scheiber R, Reigber A,.. Estimation of the surface velocity field of the Aletsch glacier using multibaseline airborne SAR interferometry[J]., 2009, 47(2): 419-430.
[7] Prats P, Reigber A, Mallorqui J,.. Estimation of the temporal evolution of the deformation using airborne differential SAR interferometry[J]., 2008, 46(4): 1065-1078.
[8] Macedo K, Scheiber R, and Moreira A. An autofocus approach for residual motion errors with application to airborne repeat- pass SAR interferometry[J]., 2008, 46(10): 3151-3162.
[9] Reigber A, Mercer B, Prats P,.. Spectral diversity methods applied to DEM generation from repeat-pass P-band InSAR[C]. In Proceedings of 6th European Conference on Synthetic Aperture Radar (EUSAR’06), Dresden, 2006.
[10] 钟雪莲. 机载重轨干涉SAR残余运动估计方法研究[D]. [博士论文], 中国科学院电子学研究所, 2011.
Zhong Xue-lian. Residual motion estimation for airborne repeat- pass interferometric SAR[D]. [Ph.D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2011.
[11] Zhong Xue-lian, Guo Hua-dong, Xiang Mao-sheng,.. Residual motion estimation with point targets and its application to airborne repeat-pass SAR interferometry[J]., 2012, 33(3): 762-780.
[12] 钟雪莲, 向茂生, 岳焕印, 等. 基于点目标自动提取的机载SAR图像残余运动估计方法[J]. 高技术通讯, 2011, 21(11): 1157-1163.
Zhong Xue-lian, Xiang Mao-sheng, Yue Huan-yin,.. Residual motion estimation in airborne SAR images based on automatic point target selection[J].,2011, 21(11): 1157-1163.
[13] Prats P, Reigber A, and Mallorqui J. Interpolation-free coregistration and phase-correction of airborne SAR interferograms[J]., 2004, 1(3): 188-191.
[14] Cumming I G and Wong F H. Digital Processing of Synthetic Aperture Radar: Algorithm and Implementation[M]. Norwood, MA, USA,the Artech House, 2005: 111-112.
[15] Fornaro G, Sansosti E, and Lanari R. Role of processing geometry in SAR raw data focusing[J]., 2002, 38(2): 441-453.
[16] Applanix Technical Product Description[OL]. http://www. applanix.com/media/downloads/products/specs/POSAV_5_ Specifications_2005. pdf, 2005.
Two Factors Influencing Residual Motion Estimation in Airborne SAR Images with MTPT
Zhong Xue-lian Chen Ren-yuan Yang Ran Wu Tao
(China Electronics Technology Group Corporation No.38 Research Institute, Hefei 230088, China)
Due to the poor accuracy of navigation systems, deviations of the order of centimeters between the real and measured trajectories, called residual motion errors, frequently occur in SAR images. For airborne SAR systems with very high resolution and airborne repeat-pass SAR interferometry, the residual motion errors must be estimated and compensated. Multi-squint Technique with Point Targets (MTPT) is able to estimate the residual motion errors for an individual SAR image, but errors in the platform velocity and the slant range will deteriorate the accuracy of the method. In this paper, we validate this by performing detailed analysis of the velocity and slant range to residual motion error estimation using both simulated and real SAR data. It is also shown that MTPT is able to estimate the errors in the velocity and slant range, and it is sensitive to the phase error. Therefore, it is advised that the errors in the velocity and slant range should be removed using other precise methods before MTPT is utilized to estimate the residual motion errors.
Airborne SAR; Residual motion error; Velocity error; Slant range error
TN957
A
2095-283X(2013)02-0180-07
10.3724/SP.J.1300.2013.20095
钟雪莲(1980-),女,安徽青阳人,2005年获中国科学院遥感应用研究所硕士学位,2011年获中国科学院电子学研究所博士学位,现为中国电子科技集团公司第三十八研究所工程师,研究方向为SAR信号处理和机载重轨干涉SAR。E-mail: sherryzxl@163.com

陈仁元(1970-),男,安徽霍邱人,中国电子科技集团公司第三十八研究所高级工程师,研究方向为SAR信号处理。E-mail: chenrenyuan3@sina.com
杨 然(1983-),女,山东济宁人,2011年获武汉大学博士学位,现为中国电子科技集团公司第三十八研究所工程师,主要从事SAR信号处理工作。E-mail: yangran322@163.com
吴 涛(1981-),男,湖北仙桃人,2008年获中国科学院遥感应用研究所博士学位,现为中国电子科技集团公司第三十八研究所高级工程师,研究方向为SAR图像处理、目标检测和识别。E-mail: hbxtwt@163.com

2012-12-12收到,2013-01-14改回;2013-01-21网络优先出版
国家高技术发展计划“863”项目(2011AA120404)资助课题
钟雪莲 sherryzxl@163.com

