利用相位差变化率的机载无源定位跟踪改进算法

李望西 黄长强 王 勇 韩 统 唐传林 蚩军祥

(空军工程大学航空航天工程学院 西安 710038)

1 引言

随着美国F-22, F-35以及T-50等新一代隐身战机的成功研制和装备运用，隐身对抗将成为未来空战的重要形式。由于采用雷达隐身技术，在空战对抗中对敌采用主动雷达探测时，不仅雷达探测性能下降，难以在远距发现目标，而且容易暴露自身的雷达辐射信号，一旦被对方利用将会对载机形成巨大威胁。而采用机载无源定位技术，通过被动测量雷达辐射信号实现定位跟踪，具有隐蔽性好，作用距离远以及抗电子干扰等诸多优势，对在隐身空战中实现“隐蔽接敌，先敌发现，先敌发射”具有重要意义[1]。

机载无源定位技术的巨大优势吸引了许多研究者的参与，目前已有研究主要集中在定位方法和跟踪算法两大方面。在定位方法上大多研究主要针对地面固定或者慢速运动目标，文献[2]基于多普勒变化率实现对固定目标的定位，文献[3]利用相位差变化率方法对海面慢速运动目标进行定位跟踪研究，文献[4]在利用角度、频率信息定位时增加了角速度信息，利用空频域信息实现了单站对运动目标的无源定位。但是该定位方法在角速度测量精度达不到mrad/s量级时定位效果不理想，参数测量要求较高。本文利用相位差变化率对角速度的放大作用，在载机上构建2维相位干涉仪布局来获取相位信息，建立了新的相位差变化率模型运用于3维空中目标的定位观测模型中。在无源定位跟踪算法方面，由于机载无源定位跟踪系统可观测性弱、参数测量初始误差大和观测方程严重非线性等特点，无源定位跟踪算法也一直是研究的热点和难点，从最初的EKF(Extended Kalman Filter)，UKF滤波及其改进算法到最近的粒子滤波[5-7]，研究者一直致力于无源定位跟踪算法稳定性、跟踪精度和收敛速度的改善和提高。在建立新的观测模型基础上，文中引入平方根UKF算法并对其进行改进，通过采用新的采样方法减少Sigma采样点数目，在保证跟踪稳定性的同时提高算法运行速度。

2 以相位差变化率替代角速度测量信息的机载无源定位原理

2.1 基于空频域信息的机载无源定位模型

基于空频域信息的无源定位充分利用了角度、角速度、频率信息可实现对运动目标的即时定位，定位模型如下[4]：

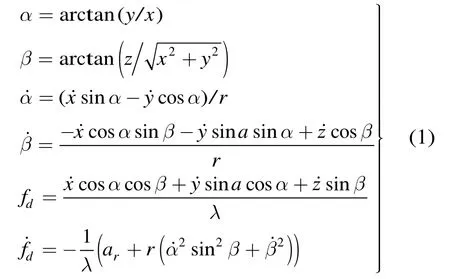
式中x,y,z为目标机与观测载机的相对坐标，r为相对距离，α,β分别为目标机相对观测载机的方位和俯仰角，,为对应的角速度，fd,为多普勒频率及其变化率，λ为辐射源波长，ar为径向加速度。

在定位模型中加入角速度信息可以实现对运动目标的定位，但是要求角速度参数测量达到mrad/s数量级，文献[4]中误差分析表明角速度是影响测距精度的主要因素，在测量误差σα=10 mrad,=1 mrad/s,=4 Hz/s 时采用最基本的EKF滤波算法进行100次Monte Carlo仿真，并将当次滤波结果相对定位误差小于 5%定义为收敛 1次，=1 mrad/s时100次仿真收敛次数仅24次，角速度测量精度提高到0.4 mrad/s时，收敛次数提高到87次，因此，要满足无源探测的定位跟踪需求，提高角速度参数精度就显得非常重要。无源定位中角速度参数可以通过角度信息求导得到[8]，这样就又需要提高角度参数的测量精度，给角度参数测量和处理带来很大压力，体现不出利用角度、角速度、频率信息定位的优势。因此，高精度角速度参数难以获取的问题限制了该方法在机载无源定位中的应用，需要寻找新的角速度参数获取方法或利用其他方式替换该参数的获取。

2.2 相位差变化率倍增角度变化率模型

相位干涉仪测角原理如图1，Eo, Ea为两个相位干涉仪阵元，Eo位于坐标原点O,T为目标点，目标波达角为α，干涉仪基线长度为d，相位差可表示为[9]

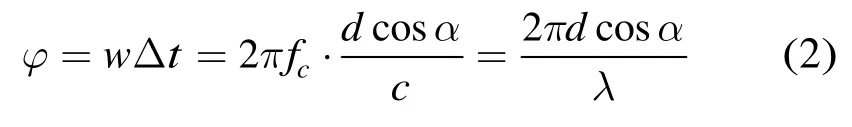
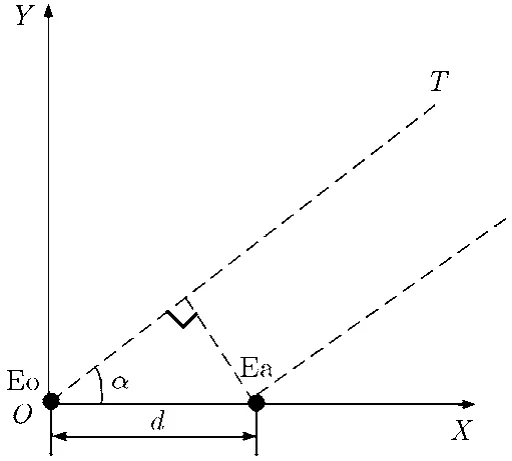
图1 相位干涉仪测角示意

式中w为来波角频率，Δt为来波到达Eo, Ea两个阵元的时间差，fc为来波频率，c为光速。

求导后得相位差变化率为

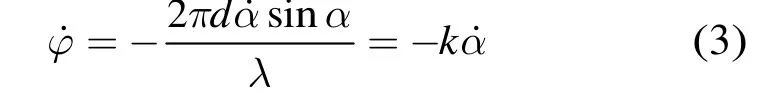
式中k=2πds inα/λ=f(d,λ,α)与d,λ,α有关，为角速度的倍增系数。可以看出k值与基线长度成正比，与辐射电磁波波长成反比。假设在α=3 0°时开始无源测距，λ=0.03 m,d=8 m，则k=838即=-838，当测角误差=0.03mrad/s，对的测量误差可放宽838倍至25.14 mrad/s，并且当载机采取并行侧向接敌时，随着载机和目标距离的拉近，放大倍数将随着目标波达角α的增大而增大。因此在公式中用替换，可降低参数测量难度，提高测量和定位精度。

2.3 基于2维相位干涉仪的无源定位模型

考虑通过在载机上布置相位干涉仪获取相位差变化率信息来替换模型中的角速度信息，在载机平台上配置3个天线，构成相互垂直的2维干涉仪定位系统，如图2所示。

假定α,β分别为目标方位和俯仰角，βx,βy和βz(β+βz=9 0°)分别是观测站O，目标T的连线和X轴，Y轴以及Z轴之间的夹角，φx和φy分别是天线A,B与天线O之间的相位差，dx和dy分别是基线OA和OB长度，λ为接收目标信号的波长。显然βx和βy是OT的两个方向余弦。由相位差定义得

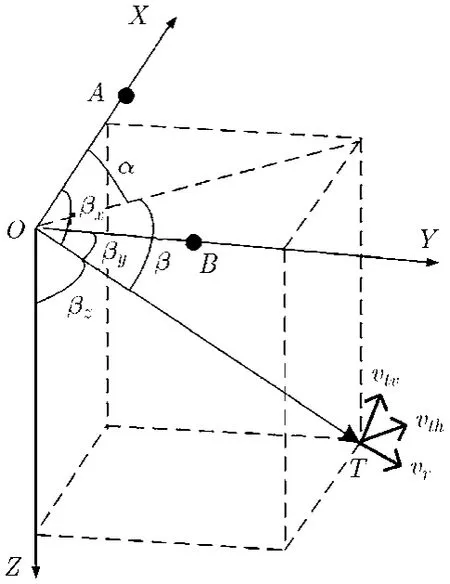
图2 2维相位干涉仪布局示意图

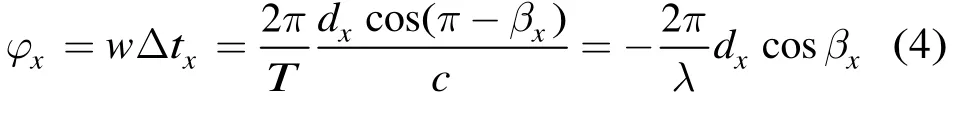
由图2中方向余弦与俯仰和方位角的关系得

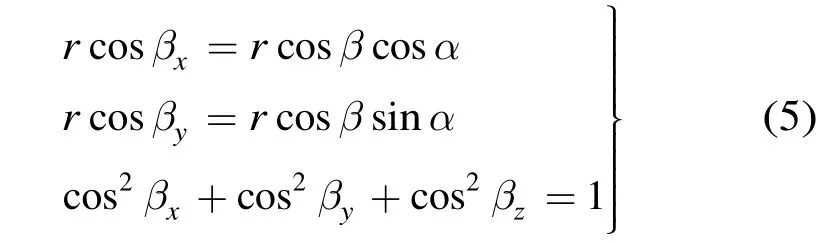
代入式(4)得φx,φy后，分别求导得到对应的相位差变化率为

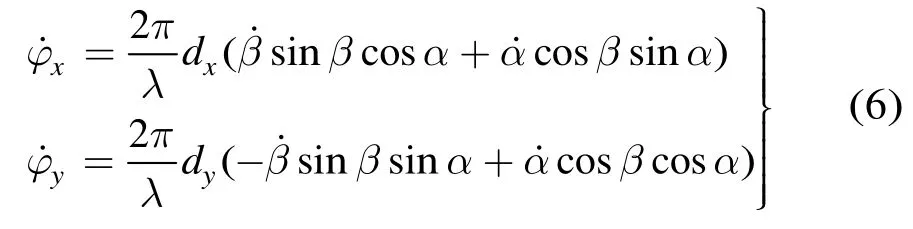
3 基于SSUT变换的平方根UKF机载无源定位跟踪算法

从UKF算法中可以看出UT变换的计算量与Sigma点个数成正比，标准的UKF算法一般采用对称采样方法进行Sigma点采样，对于状态维数为n的系统，采用对称采样方法 Sigma点采样个数为2n+1，而研究表明，对于n维状态最少可用n+1个最小斜Sigma点(minimal skew sigma)逼近。为了减少计算量，提高算法效率以满足无源定位算法实时性需求，本文考虑基于简化球形分布Sigma点采样方法进行采样点的选取，简化球形分布采样对于任意分布至少达到2阶截断精度，对于高斯分布可达到3阶的截断精度[10,11]。同时在UKF滤波过程中，利用协方差阵参加迭代运算，在迭代过程中往往由于计算误差等因素的影响，致使滤波协方差阵不对称或负定，从而导致滤波器发散，影响滤波算法的收敛速度和稳定性。在采用简化球形分布采样的基础上，结合平方根UKF算法提出基于简化球形分布采样的平方根UKF算法。为方便描述，文中简称为SSSRUKF算法(Simplex Spherical distribution Square Root UKF)，结合参考文献[12]，此处进行简化，将SSSRUKF滤波过程分为3步：

步骤1初始化

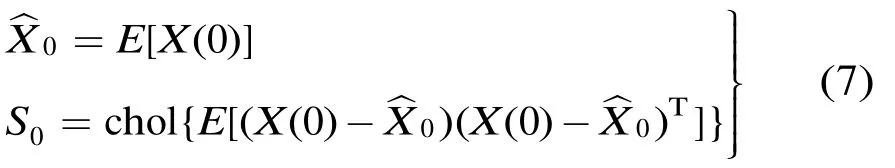
步骤2简化球形分布Sigma点采样和时间更新

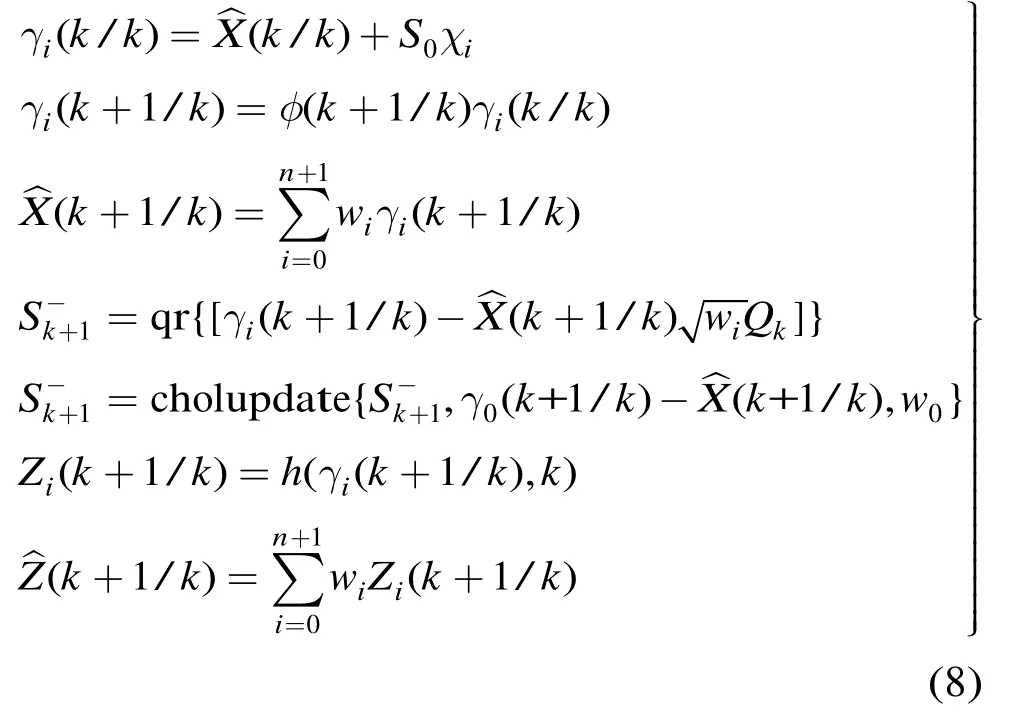
步骤3测量更新

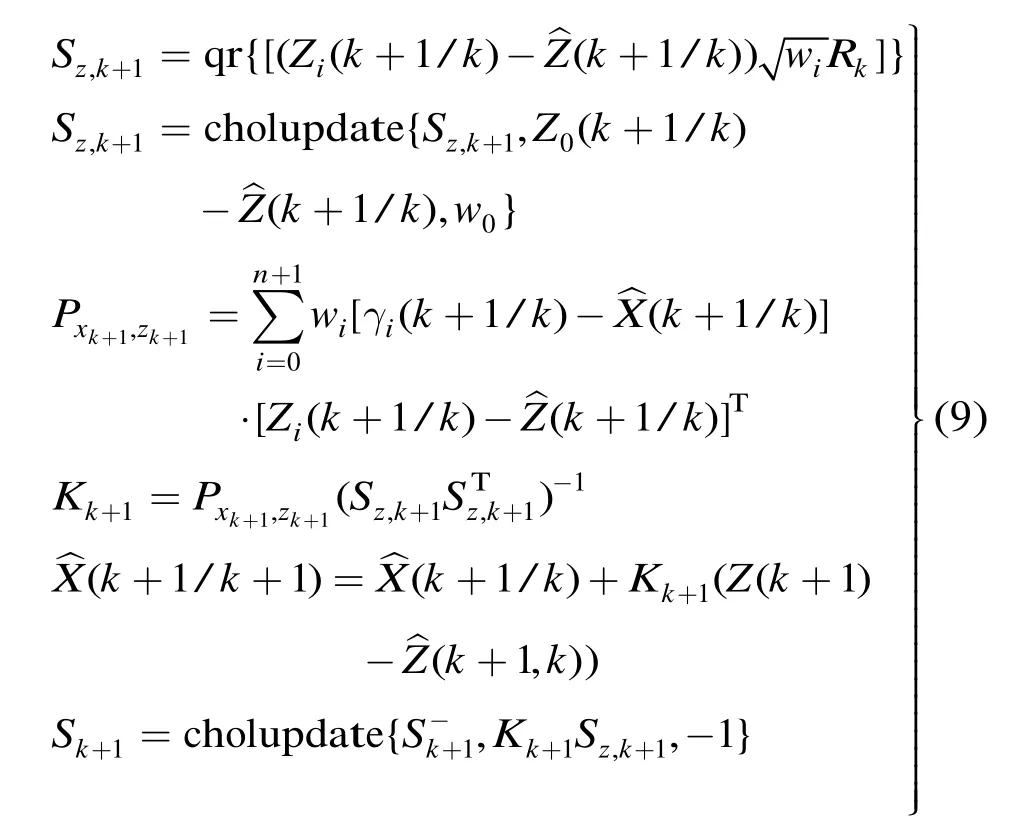
需要说明的是，算法中chol表示Cholesky分解，qr和cholupdate分别表示QR分解和Cholesky一阶更新，为Matlab中的标准指令。

4 仿真

为了检验新的定位模型和跟踪算法的有效性，本节采用Monte Carlo仿真对比实验来评估新模型和算法的定位跟踪效果。实验结果的评价指标采用目标位置状态估计相对距离误差RRE，定义为

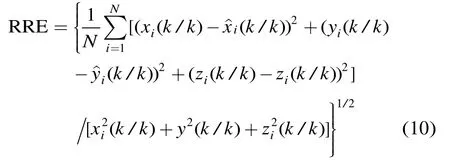
式中N为Monte Carlo仿真次数，i为第i次仿真，Xi(k/k),(k/k)为第i次运行时k时刻目标状态的真值及估计。

假定观测载机初始位置为(0 km, 0 km, 8 km)，以300m/s的速度沿X轴飞行，目标初始位置为(200 km, 20 km, 10 km)，目标速度在3个坐标轴的投影为(-300m/s, 0m/s, 0m/s)，目标一直沿X轴负向作匀速直线运动，辐射频率为10 GHz，跟踪起始时刻目标位置的滤波初值(190 km, 15 km, 9 km)，假设该滤波初值通过预警机，地面或者天基情报信息支援系统获取并传递给载机，滤波采样时间T=1 s。仿真分为两组进行，第1组主要对比分析新观测模型和原模型跟踪效果的差异，第2组仿真主要对比分析基于简化球形分布的 SSSRUKF滤波算法和EKF, UKF及SRUKF(Square Root Unscented Kalman Filter)算法在不同的观测精度条件下的跟踪滤波性能。

(1)不同定位模型目标定位跟踪效果仿真 假设采用不同定位模型的参数测量精度如下：

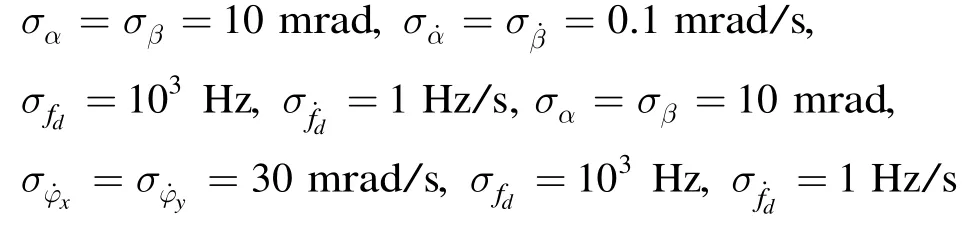
采用改进的SSSRUKF滤波算法，主要对比不同定位模型的跟踪效果，仿真结果如图3-图5及表1所示。

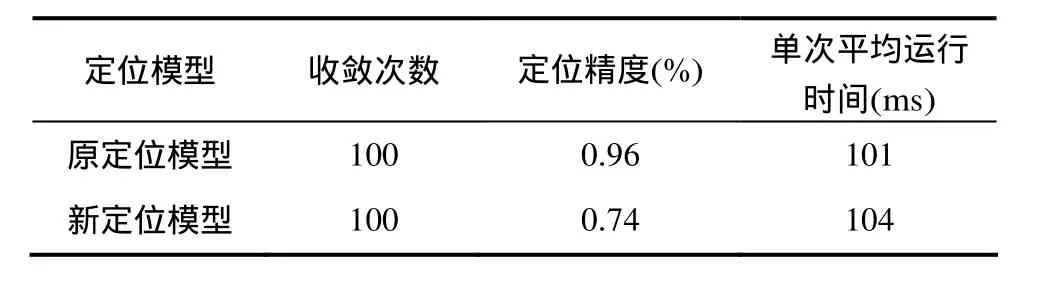
表1 不同模型Monte Carlo仿真统计结果

由仿真结果可以看出，利用相位差变化率的定位模型与原模型相比，在一定的参数测量精度下都能保证收敛，运行时间也相差不大，但是新模型的目标位置和速度跟踪误差降低，定位精度有所提高，相对定位误差降低了0.22%，新模型在60 s左右开始收敛，进入稳定跟踪，收敛速度相对较快。按照2.2节的假设条件838倍的放大率还可以进一步放宽相位差变化率的测量误差，保证在较低的参数测量条件下取得更好的定位精度。

(2)不同滤波算法目标定位跟踪效果仿真 假设有如下3种不同参数测量精度：

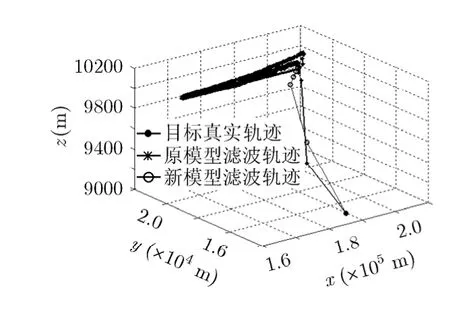
图3 目标位置跟踪结果

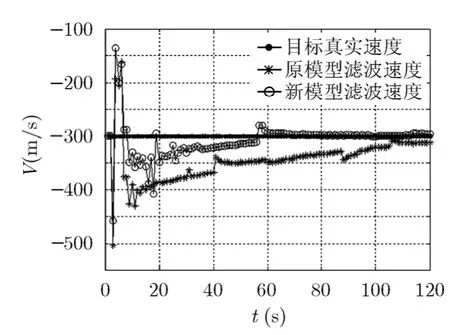
图4 目标速度跟踪结果

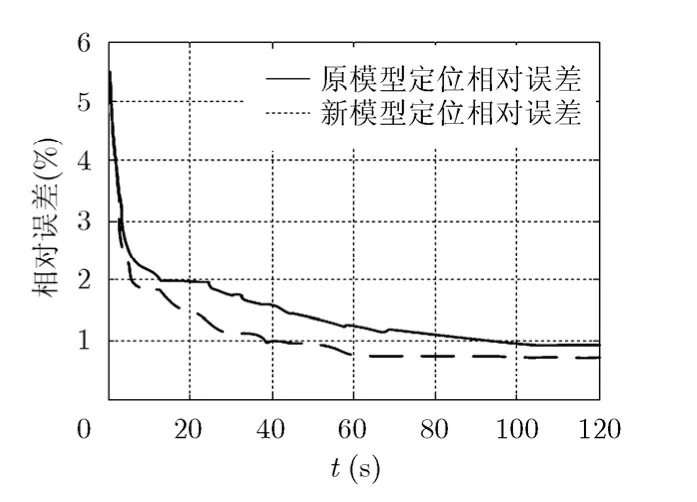
图5 目标定位跟踪相对误差

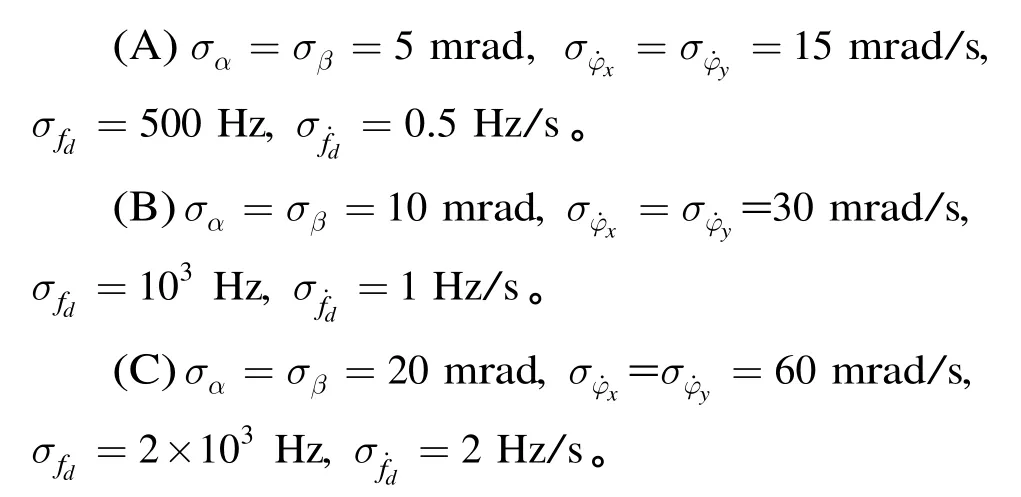
在不同的参数测量精度条件下运用不同的滤波算法进行Monte Carlo仿真，结果如图6和表2所示。

由以上仿真结果可知，虽然 SRUKF算法比UKF和EKF算法的单次运行时间长，但是UKF,SRUKF在收敛后的定位精度比EKF算法的定位精度高；在观测精度较高时，各算法的性能均有较好的表现，但随着观测精度的逐渐降低，各算法的性能开始发生变化，收敛速度变慢，滤波发散次数开始增多，稳定性下降，相比之下UKF和SRUKF在收敛速度、收敛精度、稳定性上均优于EKF。但是随着观测误差的进一步加大，UKF算法由于存在数值计算舍入误差引起误差协方差矩阵负定的问题，稳定性开始大幅下降。而SRUKF算法采用误差协方差矩阵的平方根代替协方差阵参与递推运算，提高了滤波算法的运行效率、保证了数值稳定性。采用简化球形分布 SSUT变换进行 Sigma点采样的SSSRUKF算法，参与滤波计算采样点由对称分布的2n+1降为n+2，计算量大大减小，在保证算法稳定性的同时提高了算法运行效率。

5 结束语

在对运动目标的动态定位跟踪中，利用相位差变化率替换角速度机载无源定位方法可以取得比原定位模型更好的目标跟踪精度，降低了无源定位参数获取难度，与作者在文献[9]中静态定位误差的分析结果相符，而且仿真表明新的定位方法在定位相对误差降低 0.22%的同时，计算量基本没有发生变化。同时改进的SSSRUKF算法结合了SRUKF算法和SSUT变化的优点，利用方根形式增强了滤波的稳定性，通过减少采样点提高算法的收敛速度，单次滤波运算时间比SRUKF降低了19%，从稳定性，收敛精度和速度等多方面衡量总体性能优于EKF, UKF和SRUKF算法，是一种稳定的定位跟踪算法。本文采用的定位方法对机载无源定位的工程实践有一定的参考价值，跟踪滤波算法也可以应用于其他非线性滤波问题，下一步还需研究该方法对机动目标的定位跟踪效果。

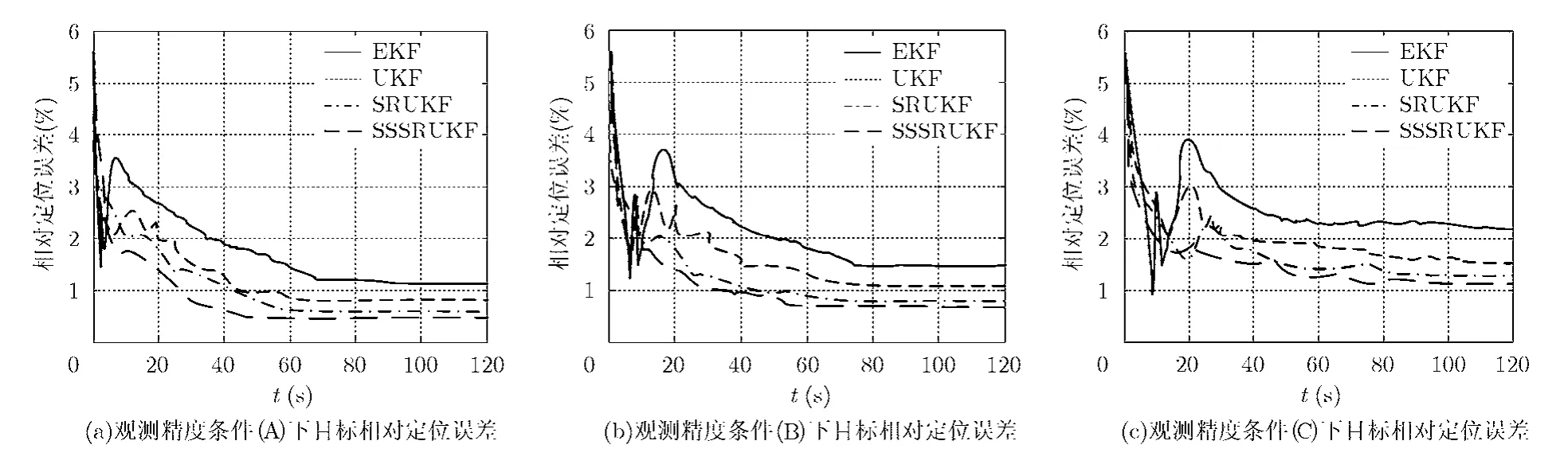
图6 不同观测精度条件下不同跟踪算法相对定位误差

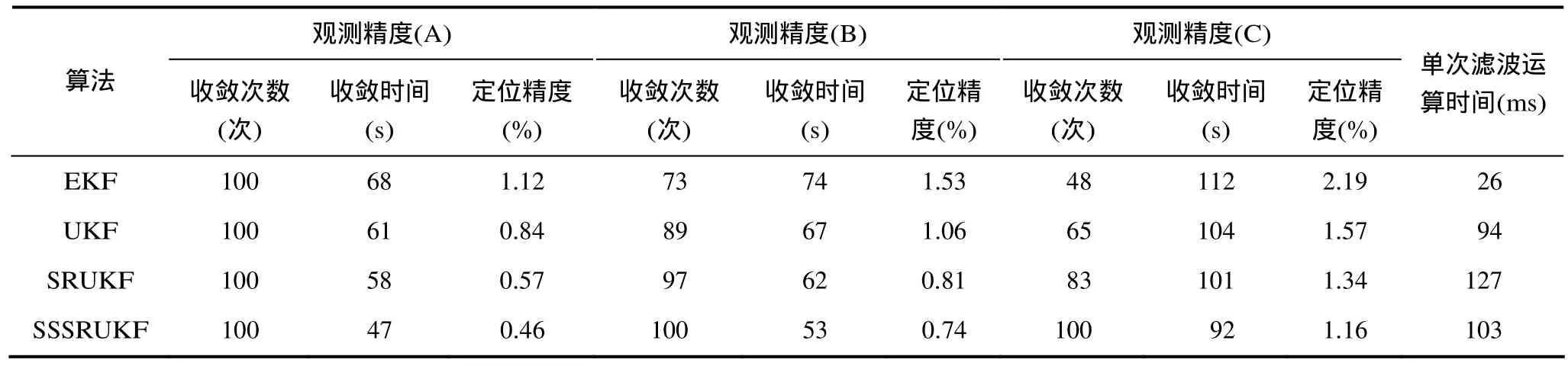
表2 不同观测精度条件下不同跟踪算法性能对比

[1]杨晓君, 陆芳, 郭金库, 等. 模糊单站无源定位方法[J]. 清华大学学报(自然科学版), 2011, 51(1): 25-29.

Yang Xiao-jun, Lu Fang, Guo Jing-ku,et al.. Fuzzy single observer passive locating algorithm[J].Journal of Tsinghua University(Natural Science Edition), 2011, 51(1): 25-29.

[2]平殿发, 司文健, 苏峰. 基于多普勒变化率的机载无源定位方法研究[J]. 中国雷达, 2010, 29(4): 4-6.

Ping Dian-fa, Si Wen-jian, and Su Feng. Research on airborne passive location based on Doppler rate-of-change[J].China Radar, 2010, 29(4): 4-6.

[3]单月晖. 空中观测平台对海面慢速目标单站无源定位跟踪及其关键技术研究[D]. [博士论文], 长沙: 国防科学技术大学,2002.

Shan Yue-hui. Research on tracking and key technology of passive location on offing slow target from airborne observation platform[D]. [Ph.D. dissertation], Changsha:National Defense University of Science and Technology, 2002.

[4]郁春来. 利用空频域信息的单站无源定位与跟踪关键技术研究[D]. [博士论文], 长沙: 国防科学技术大学, 2008.

Yu Chun-lai. Research on crucial technologies for single observer passive location and tracking via spatial-frequency domain information[D]. [Ph.D. dissertation], Changsha:National Defense University of Science and Technology, 2008.

[5]赵国伟, 李勇, 李滔. 基于MVEKF算法的机载单站无源定位[J]. 西北工业大学学报, 2007, 25(1): 113-116.

Zhao Guo-wei, Li Yong, and Li Tao.Algorithm for airborne single passive location based on MVEKF[J].Journal of Northwestern Polytechnical University, 2007, 25(1): 113-116.

[6]管旭军, 芮国胜, 康锡章. 基于UKF的机载无源定位算法[J].航天控制, 2005, 23(5): 13-16, 41.

Guan Xu-jun, Rui Guo-sheng, and Kang Xi-zhang. A passive location algorithm for airborne observer based on UKF [J].Aerospace Control, 2005, 23(5): 13-16, 41.

[7]刘学, 焦淑红. 拟蒙特卡罗自适应粒子滤波的机载无源定位算法[J]. 西安交通大学学报, 2011, 45(9): 35-39.

Liu Xue and Jiao Shu-hong. Quasi monte-carlo adaptive particle filter for airborne passive location[J].Journal of XiAn Jiao Tong University, 2011, 45(9): 35-39.

[8]孙仲康, 郭福成, 冯道旺. 单站无源定位跟踪技术[M]. 北京:国防工业出版社, 2008, 239-241.

Sun Zhong-kang, Guo Fu-cheng, and Feng Dao-wang. Passive Location and Tracking Technology by Single Observer [M].Beijing: National Defense Industry Press, 2008: 239-241.

[9]李望西, 黄长强, 王勇, 等. 一种利用相位差变化率的机载单站无源定位方法[J]. 电讯技术, 2012, 52(1): 13-17.

Li Wang-xi, Huang Chang-qiang Wang Yong,et al.. An airborne single observer passive location using phase difference rate-of-change[J].Telecommunication Engineering,2012, 52(1): 13-17.

[10]Julier Simon J and Uhlmann Jeffrey K. Unscented filtering and nonlinear estimation[J].Proceedings of the IEEE, 2004,92(3): 401-422.

[11]Van der Menve Rudolph and Wan Eric A. The square root unscented kalman filter for state and parameter estimation[C]. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing, New York, 2001:3461-3464.

[12]周峰, 焦淑红. 基于平方根 UKF的机载无源定位算法[J]. 应用科技, 2010, 37(11): 40-44.

Zhou Feng and Jiao Shu-hong.A passive location algorithm for the single airborne observer based or square root UKF[J].Applied Science and Technology, 2010, 37(11): 40-44.