基于忆阻器的混沌电路研究
吴迪,胡岩
(沈阳工业大学电气学院,辽宁 沈阳 110870)
1 引言
基本电路理论中,常见的基本电路元件有:电阻、电感、电容。这些元件的特性是用电压、电流、磁通和电荷这4个物理量来表示。1971年,蔡少棠(L.Chua)先生指出应该有六个数学关系来联接这四个基本的物理量[1]。但现在只有五个确定的关系,从对称的观点看,推测出有第四种基本元件存在,称之为忆阻器,用来反映电荷和磁通之间的函数关系。2008年惠普实验室的成员成功地实现纳米级电子元件,已有文献报道了一些记忆器件的建模成果,例如文献[2]中只是综述了忆阻器和忆阻系统概念的产生与发展过程,实现忆阻功能的几种模型与机理。阐述了忆阻器和忆阻系统在模型分析、生物记忆行为仿真、基础电路和器件设计方面的应用前景。文献[3]是对忆阻器的应用及其未来的展望做出论述。Strukov[4]等最早提出边界迁移模型用于实现忆阻器具有的电路特性,认为电极间的半导体薄膜(厚度D)由于基体中载流子浓度不同而分为低电阻的高掺杂浓度区和高电阻的低掺杂浓度区,结构两端加载的偏电压驱使高、低掺杂浓度区间的边界发生迁移,致使结构对外呈现随外加电压时间作用而变化的电阻[5,6],这部分理论认为,外偏压的施加影响了载流子迁移过程,从而改变了迁移几率,导致材料电阻状态发生变化而产生忆阻性。
非线性电路中的混沌现象是最早引起人们关注的现象之一,在非线性电路中能够得到很好的混沌实验结果,蔡氏混沌电路[7-9]就是一个典型的混沌电路。在理想条件下观察出现的波形,本文用忆阻器代替蔡氏电路中非线性部分,采用 pspice对电路进行仿真[10],其波形与理想的蔡氏电路波形进行比较。
2 忆阻器Simulink模型
忆阻器独特的性能及应用前景引起了强烈关注。现在物理忆阻器有很多种,但大多数研究者认为获得物理模型是困难的,目前这个阶段,主要是根据他们的理论模型进行分析和研究。介绍忆阻器理论基础,研究了理想(线性杂质迁移)的电荷控制忆阻器和磁通量控制忆阻器模型,建立忆阻器的Simulink模型。
惠普忆阻器的物理模型,它是由将两层纳米级的二氧化钛薄膜夹在两个铂片内,其中一部分有氧空位,表现半导体特性,另一部分没有掺杂,可以看作绝缘体。

图1 HP忆阻器实现原理图
图中,D是夹层宽度,W是“掺杂”部分宽度,掺杂宽度和器件通过的电量的方向和大小有关,可以表征器件的阻抗(resistance),一般来说,阻抗R和W/D正相关。
忆阻器的电阻Rm(t)是掺杂区和末掺杂区电阻之和。

其中ROFF和RON分别是w(t)=0和w(t)=D时忆阻器电阻的极限值,通常这两者的比值ROFF/RON=102~103,如图所示w(t)是掺杂层的厚度,D是两层二氧化钛薄膜的总厚度,x(t)是w(t)与D的比值,在理想(线性杂质迁移)的模型中。

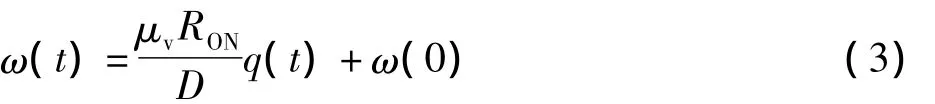
将(3)代入(1)中得到电荷控制的忆阻的忆阻器的电阻值公式。

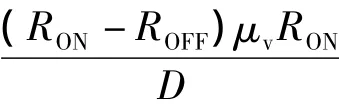

基于忆阻器理论基础。建立了忆阻器的Simulink模型(图2)。忆阻器由这几个模块构成,基本参数模块(RON,ROFF,X0),窗函数模块(f(x))和显示模块(out)等。当忆阻器为理想情况时,窗函数f(x)=1。
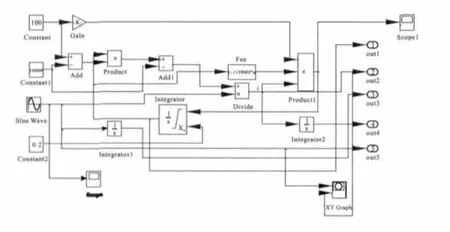
图2 simulink仿真模型
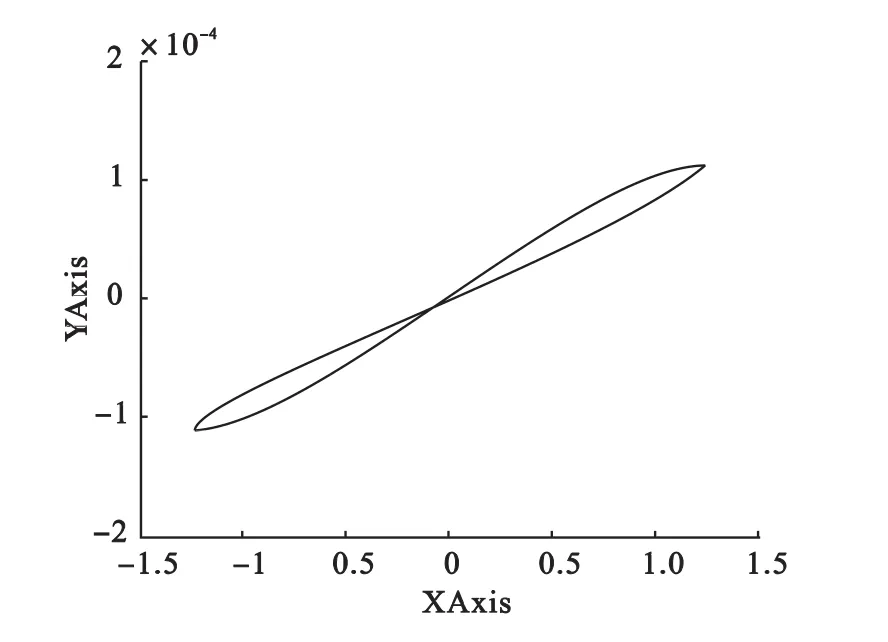
图3 输出电流与输入电压的关系
3 蔡氏电路的构成
蔡氏电路是一个典型的混沌电路。蔡氏电路实验电路图如图4所示。电路中的电感L和电容C1、C2并联构成一个振荡电路。R是一个有源非线性负电阻元件,电感L和电容C2组成一损耗可以忽略的谐振回路;可变电阻R和电容C1串联将振荡器产生的正弦信号移相输出。
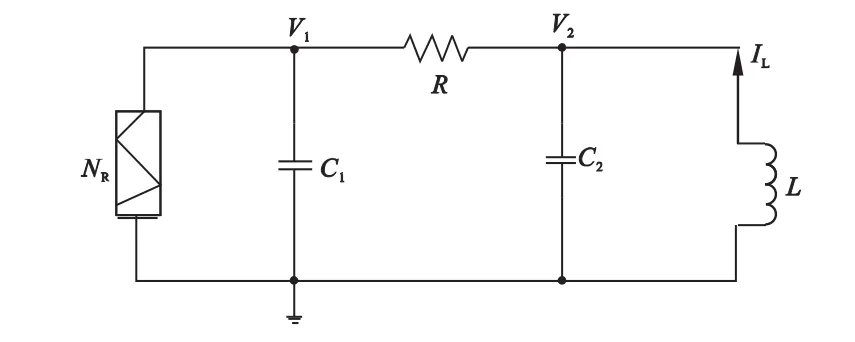
图4 蔡氏电路图
蔡氏电路的状态方程式为:
式中UC1,UC2分别为电容C1,C2上的电压;il为电感L上的电流,G=1/R0为电导;g为R的伏安特性函数。
当R为线性电阻时,g为常数,电路为一般振荡电路,此时把C1和C2两端的电压分别输入到示波器的x,y轴,显示的图形是椭圆形;当R为非线性负电阻时,其伏安特性如图2,此时把C1和C2两端的电压分别输入到示波器的x,y轴,调节G的值就会观察到不同的混沌现象。
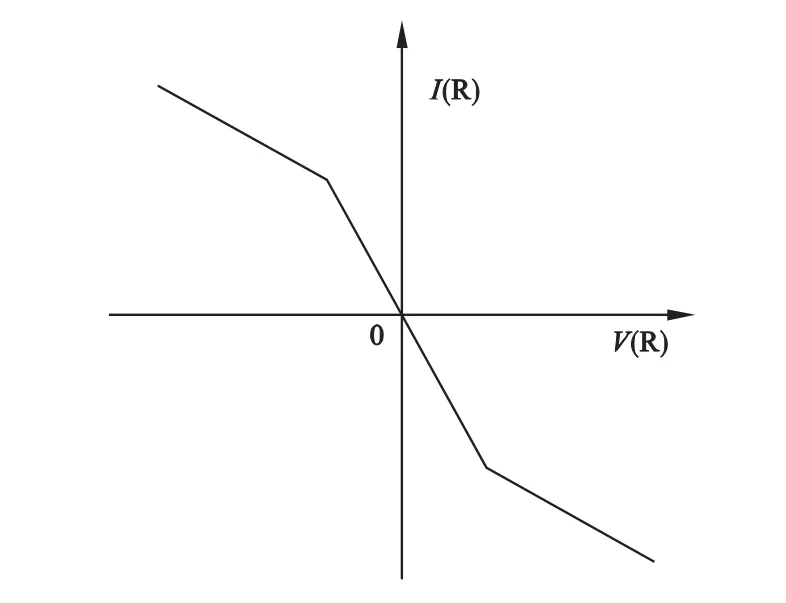
图5 有源非线性负电阻伏安特性曲线
4 含有忆阻器的蔡氏电路实现
把忆阻器的蔡氏电路放到Pspice中仿真,电路按照蔡氏电路接法来接,只是把蔡氏电路中的非线性部分换成上一章搭建的忆阻器模型。电路图如图8所示。

图6 IV分析仪测量有源非线性负电阻伏安特性电路图

图7 理想中的蔡氏波形
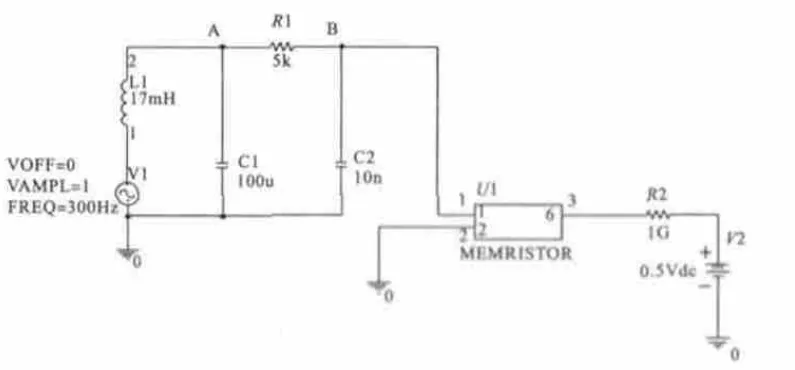
图8 含有忆阻器的蔡氏电路

图9 含有忆阻器混沌波形
5 混沌电路的几种应用
基于混沌电路的特性,它在许多领域中有重要的应用。但由于目前混沌学仍处于研究阶段,故其应用并不完善,出现的一些问题还有待解决。
(1)保密通信中的应用:使强度更大的混沌信号和真实信号同步,由于混沌信号具有信号频谱宽、类似噪声、随机不可预测等特性,当真实信号被混沌信号所掩盖时,攻击者就很难从传输信号中分离出原始真实信号[9]。
(2)自动控制中的应用:考察非线性混沌系统的输出信号与输入信号的自反馈耦合,或者从系统外部强迫注入某一周期信号,或者直接将系统自身的输出信号取出一部分经过一定的时间延迟后再反馈到原混沌系统中去.作为控制信号,通过调节控制因子及控制信号的大小实现稳定控制。
(3)传感应用:混沌具有初值敏感性,当其结构参数稳定时,初始值与动力轨道在一定的时间内是一一对应的,而且对于微小的初值变化,其运动轨迹就会出现指数分离。若初值细微变化是由混沌系统中的传感元件随被测参数变化而引起的。这种混沌型传感器具有很高的灵敏度和分辨率,特别适用于微应变测量;微量变化物参数的测量。
6 结论
本文首先介绍了忆阻器的原理及其模型,并用simulink根据忆阻器公式仿真出其IV特性曲线,然后介绍了蔡氏电路的基本概念及其应用,并给出蔡氏电路的理想波形。根据蔡氏电路,用忆阻器代替非线性部分,可以混沌现象中电路是非周期性的,时而稳定,时而混乱。基于混沌电路的这些特性,它将在许多应用领域有重要的应用,更多的应用将依赖于对混沌理论的研究和实验分析。
[1]CHUA L O.Memristor-the missing circuit element[J].IEEE Trans Circuit Theory,1971,18(5):507-519.
[2]蔡坤鹏,王睿,周济.第四种无源电子元件忆阻器的研究及应用进展[J].电子元件与材料,2010,29(4).
[3]张荣芬,邓朝勇,傅兴华.可记忆电阻器及其应用展望综述[J].计算机工程与科学,2011,33(2).
[4]Strukov D B,Snider G S,Stewart D R,Williams R S.The missing memristor found;Nature,2008,453(7191):80-81.
[5]张旭,周玉泽,闭强,等.有边界条件的忆阻元件模型及其性质[J].物理学报,2010,59(9).
[6]Wey,T.A.(Dept.of Electr.& Comput.Eng.,Lafayette Coll.,Easton,PA,United States);Jemison,W.D;Variable gain amplifier circuit using titanium dioxide memristors;IET Circuits,Devices & Systems,2011,5(1):59-65.
[7]蒋国平,陈艳云.蔡氏混沌非线性电路及其频率特性的研究.电气电子教学学报,2002,(10).
[8]李小春,朱双鹤,王国红,等.混沌信号产生电路的研究[J].空军工程大学学报(自然科学版),2001(10).
[9]王玉芳,杨峰.一个非自治混沌电路的同步实现及其保密通信应用[J].山东师范大学学报(自然科学版),2007(3).
[10]刘英明,马艳萍,王东方.混沌电路的仿真研究[J].佳木斯大学学报(自然科学版),2006(6).

