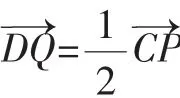立足几何模型 放飞空间想象——感悟2013年湖北省高考理科数学第19题
☉湖北省武汉市黄陂区第一中学 翁华木
一道好的高考试题,往往呈现出形式独特、内涵深刻、给人启迪的经典,凝聚了命题者的智慧.刚刚落下帷幕的2013年湖北省高考理科数学第19题就是这样的一道好题,命题风格上保持适度创新,规避题型套路,既有探究结论关系的判断,又有揭示数学本质的推理,吸引着解答者探究与思考.下面给出笔者对本道高考试题探究的亲历过程,与大家交流.
一、题目展现
如图1,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
(Ⅰ)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明.
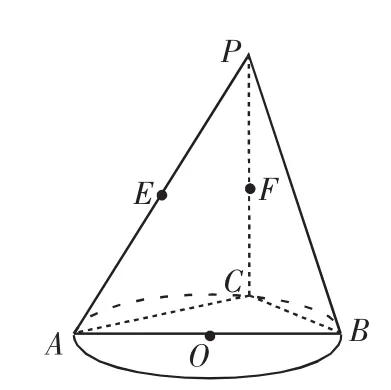
图1
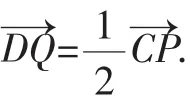
初读试题,创新的命题风格扑面而来:没有了常见的棱柱体,也不是熟知的三棱锥.命题图形的设计,给出的是一个组合体,其中下底面是一个圆形,圆形的上面是一个内涵丰富的三棱锥.问题求解的设计,一是判断线面关系并加以证明,需要解答者结合图形进行探究,增加了思维的难度;二是求证三角函数等式成立,即体现了立体几何和三角函数知识的交汇,而颇具创意地将空间的三类角(即异面直线所成的角、直线与平面所成的角、二面角的平面角)融合在同一道题目之中,增添了解题的智慧.
二、解题探究
读着题目的条件,盯着给出的图形,想着解题的方向,两个思维的疑点很快在脑海里浮现,挥之不去,成为突破问题解答的焦点.
1.涉及两个平面相交的公共直线在哪里
本题第(Ⅰ)问是判断直线l与平面PAC的位置关系,而直线l是平面BEF与平面ABC的交线,由命题者给出的几何图形我们看到,平面BEF与平面ABC只有一个交点B.解题者的第一个感觉是:平面BEF与平面ABC的交线l在哪里?
(1)回归课本——寻源
展开思维联想,搜索知识储备,人教社教材《数学2·必修》(A版)第二章“点、直线、平面之间的位置关系”中的公理3立刻跳跃出来:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
根据公理3,我们找到了平面BEF与平面ABC的交线l,它是定位在过两个平面的公共点B的一条公共直线.
(2)尝试解答——判断
面对几何图形,提取有效信息,由题设条件E,F分别是PA,PC的中点,可知EF是△PAC的中位线,在已有的解题经验中,中位线知识给出的是平行信息.经过尝试和推理,不难发现问题的结论:直线l∥平面PAC.
下面的解题思路就是利用空间的线面平行关系,推证这个结论的成立.
解析:(Ⅰ)直线l∥平面PAC,证明如下:
如图2,连接EF,BE,BF.
因为E,F分别是PA,PC的中点,所以EF∥AC.
又EF⊄平面ABC,且AC⊂平面ABC,所以EF∥平面ABC.
而EF⊂平面BEF,且平面BEF∩平面ABC=l,所以EF∥l.
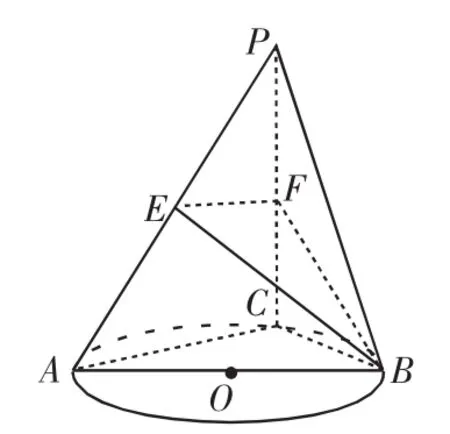
图2
因为l⊄平面PAC,EF⊂平面PAC,所以直线l∥平面PAC.
2.关联三角函数等式的几何模型在哪里
本题第(Ⅱ)问是证明涉及三个空间角的三角函数等式sinθ=sinαsinβ成立,其中θ是直线PQ与平面ABC所成的角,α是异面直线PQ与EF所成的角,β是二面角E-l-C的平面角.解题者的第二个感觉是:三角函数等式涉及空间的三个角,那么关联这三个角的空间几何模型在哪里?
(1)定格几何模型
立体几何中关于空间角的三角函数等式的证明,常见的解题方法是在一个空间几何模型中,每一个空间角都有一个对应的直角三角形(或任意三角形),通过三角形中三角函数关系式的对应边之间的分拆与转换,可以找到它们之间的恒等关系.例如下面的空间几何图形和结论是典型的:
如图3,已知PA,PB分别是平面M的垂线和斜线,在平面M内,过斜足B引一条直线BC,且作AC⊥BC于点C,连接PC,设∠PCA=θ,∠PBA=α,∠PBC=β,∠ABC=γ,则有
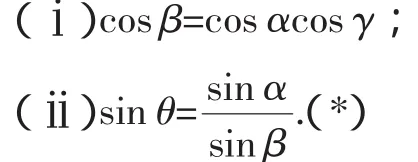
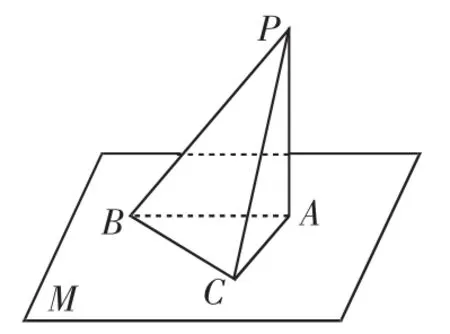
图3
不难发现,在这个几何模型中,四面体P-ABC是一个特殊的几何体,构成它的四个面都是直角三角形,有利于空间角对应的三角函数关系式的建立和线段间的转换.
回到考题给出的图形,结合对应的空间三个角,不难发现涉及三个空间角关联的空间几何体模型就是三棱锥F-BCD,它也是一个特殊的四面体,构成它的四个面同样都是直角三角形.
(2)定位空间角度
找到了问题求解的空间几何体模型之后,接下来的任务就是把题设条件给出的三个空间角定位在对应的空间几何模型之中.这个解题的过程中必须做到两点:一是准确作出对应的空间角,二是证明所作出的空间角符合题设条件的要求.
下面的解题过程就是作出对应的空间角,证明三角函数等式的成立.
解析:(Ⅱ)如图4,连接BD,由(Ⅰ)可知交线l即为直线BD,且l∥AC.
因为AB是⊙O的直径,所以AC⊥BC,于是l⊥BC.
已知PC⊥平面ABC,而l⊂平面ABC,所以PC⊥l.
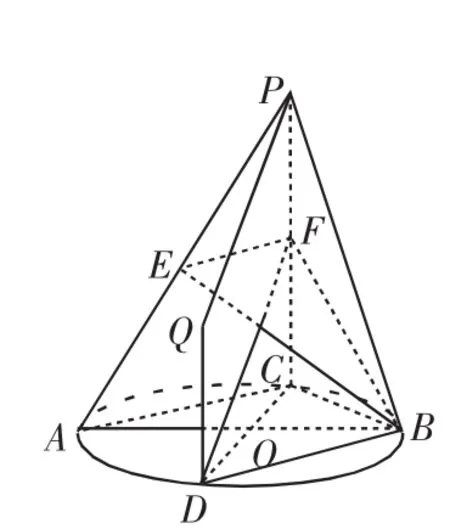
图4
而PC∩BC=C,所以l⊥平面PBC.
连接BE,BF,因为BF⊂平面PBC,所以l⊥BF,
故∠CBF就是二面角E-l-C的平面角,即∠CBF=β.
连接PQ,DF,因为F是CP的中点,CP=2PF,所以DQ=PF.
从而四边形DQPF是平行四边形,PQ∥FD.
连接CD,因为PC⊥平面ABC,所以CD是FD在平面ABC内的射影.
故∠CDF就是直线PQ与平面ABC所成的角,即∠CDF=θ.
又BD⊥平面PBC,由BD⊥BF,知∠BDF为锐角,故∠BDF就是异面直线PQ与EF所成的角,即∠BDF=α.
于是在Rt△DCF,Rt△FBD,Rt△BCF中,分别可得
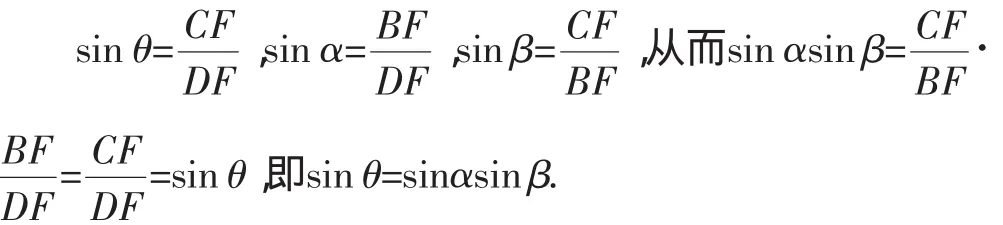
本题第(Ⅱ)问还可以用向量法给出证明,本文从略.
如果将上面(*)式的形式改写成sinα=sinβsinθ,并将其中的空间角与高考题中的空间角作一个对应,可以发现它与高考题所要证明的三角函数等式其实是同一个结论.再回到图形上,对比两个空间几何体,发现它们只是从不同的视角画出的同一个空间几何模型.至此,我们找到了2013年湖北省高考理科数学第19题的命题之源.
三、教学感悟
赏析2013年湖北省高考理科数学第19题,朴实中透视着鲜明的课改理念,平淡中显示着明确的课改方向,为立足教学一线的教师,留下更多的回味与思考.
1.追求创新,为有效课堂引入活力
新课程教育理念给我们的课堂教学提出了创新的教学模式.高三的复习备考,传统的“题海”战术,“时间”加“汗水”的付出,在应对新课程理念指导下的新高考命题时已经显出了力不从心的病态.“基础与能力并重,稳定与创新兼顾,应用与文化并举”是湖北省两年来新课程高考数学命题的特色,我们必须从根本上反思教学行为,创新教学方法,真真切切地落实高效课堂,培养学生的创新能力,提升学生的数学素养.
高三数学复习课中,每一节课教师选用的例题不在多,经典就行.通过对经典数学问题背景的探究,力争做到追根索源,对经典数学问题的解答,不仅强调结果,更要强调过程,揭示其数学问题的本质.正是由于平时教学中有对经典数学问题的探究习惯,才使我们在解题的过程中,挖掘出了2013年湖北省高考理科数学第19题的命题背景.
2.提炼信息,为有效思维指明方向
从信息论的观点来看,求解数学问题的过程,首先是对源信息的提取,然后是对信息进行变换(处理、决策),最后是对信息的反馈进行处理.面对高考试题,解答者必须首先做到快速地提取有利于问题求解的条件信息、图形信息,然后锁定思维,联想课本上归纳的性质、定理、公式,或相似的典型例题对应的解题思想与方法,这样才能寻求问题解答的突破口.
在前面探求试题解答的过程中,由条件E,F分别是PA,PC的中点,联想到了三角形的中位线性质,从而推理出了线面平行的判断.在这个从信息提取到问题解答的思维过程中,由“中点”联想到“中位线”,再推理出“线面平行”的判断,得益于对有效信息的提炼.
3.积累经验,为有效解题提供保障
新课标明确提出了使学生获得数学的基础知识、基本技能、基本思想、基本活动经验的目标要求.在高考高度紧张的情况下,如果没有平时解题经验的积淀,完全依靠考试时的“随机应变”设计出解题方法,或者试图通过观察思考突发奇想得到特殊的“巧法妙招”,既无法对一个全新的试题解法以及在解答过程中出现的困难做出预测,又无法预知自己设计的方法是否能够得到正确答案,往往会出现“做到哪里算哪里”的被动局面.因此,归纳解题范式,积累解题经验是成功解答高考试题的有效做法.