一道课本探究题的推广与应用
☉江苏省镇江中学 蒋景景
苏教版必修4第23页拓展·探究22题:“若α为锐角(单位为弧度),试利用单位圆及三角函数线,比较α,sinα,tanα之间的大小关系.”该题结构美观、证法巧妙、内涵丰富、应用广泛.现撷取其中的一部分,供大家参考.
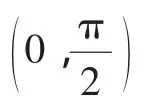
一、推广
1.结论
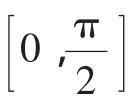
Ⅰ.当k∈[1,+∞)时,sinx≤kx;
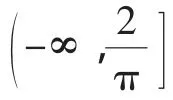
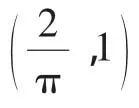
2.图示
上述结论可以从图1中得到直观的解释.
3.证明
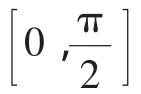
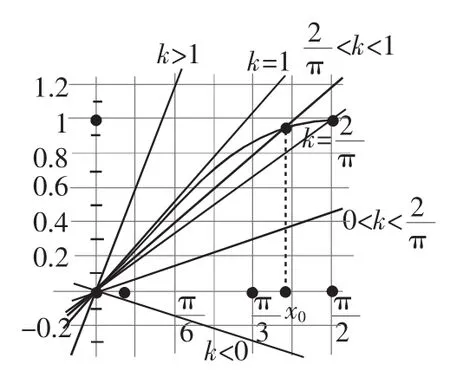
图1
当k≥0时,令h(x)=kx-sinx,则h′(x)=k-cosx.
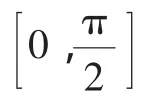
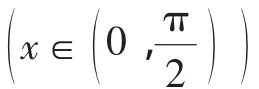
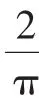
综上可知结论成立.
二、应用
例1(2008年普通高等学校招生全国统一考试全国卷(理科)第22题)
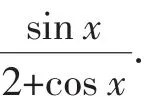
(1)求f(x)的单调区间;
(2)如果对任何x≥0,都有f(x)≤ax,求a的取值范围.
解:(1)从略.
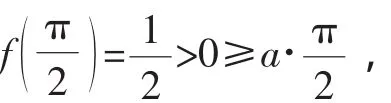
故a≤0不成立.
令g(x)=ax-f(x),则
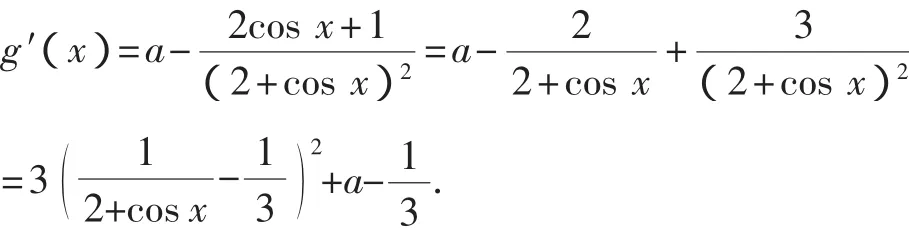

又g(0)=0,所以当x≥0时,g(x)≥g(0)=0.
即(fx)≤ax.

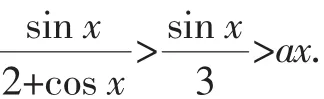
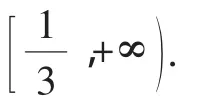
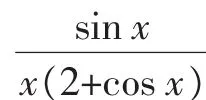
(2)本题的基点之一即是对sinx≥kx的条件探求,如果对结论Ⅱ、Ⅲ有一定的了解,则无形中提高了学生的思维起点.
例2(2012年南通市、泰州市、扬州市高三第一次调研考试第19题)
已知函数f(x)=x+sinx.
(1)设P,Q是函数f(x)图像上相异的两点,证明:直线PQ的斜率大于0;
解:(1)从略.
(2)①当a≤0时,f(x)=x+sinx≥0≥axcosx恒成立.
②当a>0时,令g(x)=f(x)-axcosx=x+sinx-axcosx,
g′(x)=1+cosx-a(cosx-xsinx)=1+(1-a)cosx+axsinx.
(ⅰ)当1-a≥-1,即0<a≤2时,g′(x)=1+(1-a)cosx+axsinx>0,
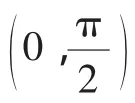
g(x)≥g(0)=0+sin 0-a×0×cos0=0,符合题意.
(ⅱ)当a>2时,由结论Ⅰ知当x∈时,sinx≤x,
故g(x)=x+sinx-axcosx≤2x-axcosx=x(2-acosx),
存在x0∈,使得2-acosx<0,即存在x0∈,使得x+sinx≤axcosx.
综上所述,实数a的取值范围为a≤2.
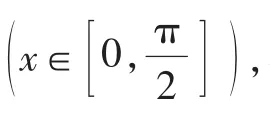
例3(2012年普通高等学校招生全国统一考试全国卷(理科)第20题)
设函数f(x)=ax+cosx,x∈[0,π].
(1)讨论f(x)的单调性;
(2)设f(x)≤1+sinx,求a的取值范围.
解:(1)从略.
(2)由f(x)≤1+sinx得f(π)≤1,即aπ-1≤1,
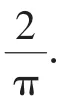
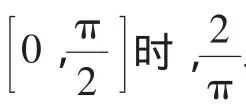
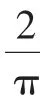
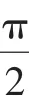
所以f(x)≤1+sinx.
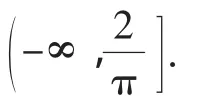
评注:(1)由特殊到一般,采用“逐步逼近”的方式大致定出a的取值范围;

