用导数证明不等式的几个技巧

☉湖北省武汉市新洲一中 李 俊

利用导数证明不等式，是高考的常考题型，尤其是证明函数背景下的不等式.笔者在教学中有一点心得体会，下面通过例题展示一下用导数证明不等式的技巧，供读者参考.

一、直接作差构造函数证明

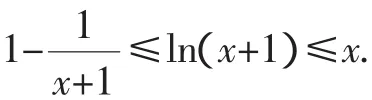
当-1＜x＜0时，f′（x）＞0；当x＞0时，f′（x）＜0.

函数f（x）的单调递增区间为（-1，0），单调递减区间为（0，+∞）.

于是函数f（x）在x=0处取得最大值f（0）=0.

因此，当x＞-1时，f（x）≤f（0）=0，即ln（x+1）-x≤0，所以ln（x+1）≤x.

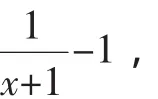
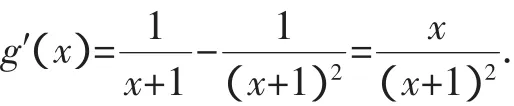
当x∈（-1，0）时，g′（x）＜0；当x∈（0，+∞）时，g′（x）＞0，g（x）的单调递减区间为（-1，0），单调递增区间为（0，+∞）.

故函数g（x）在x=0处取得最小值g（0）=0.

当x＞-1时，g（x）≥g（0）=0，

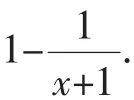
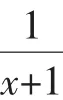
点评：用导数证明不等式最基本方法就是将不等式的一边移到另一边，然后令这个式子为一个函数，通过求导判断单调性，然后证明函数的最值大于（或小于）0.

二、利用已知函数的最值进行证明

例2 （Ⅰ）已知函数f（x）=lnx-x+1，x∈（0，+∞），求函数f（x）的最大值.

（Ⅱ）设ak，bk（k=1，2，3，…，n）均为正数，证明：

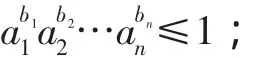
（2）若b1+b2+…+bn=1，则

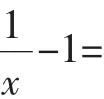
当0＜x＜1时，f′（x）＞0；当x＞1时，f′（x）＜0.

f（x）在（0，1）上是增函数，f（x）在（1，+∞）上是减函数.

故函数f（x）在x=1处取得最大值f（1）=0.

（Ⅱ）（1）由（Ⅰ）知，当x∈（0，+∞）时，有f（x）≤f（1）=0，即lnx≤x-1.

因为ak，bk均为正数，从而有lnak≤ak-1，得

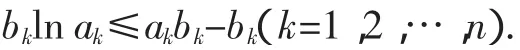
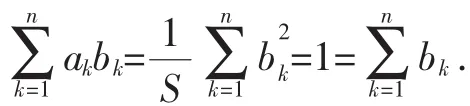
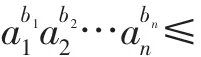
三、做商构造函数证明

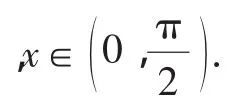
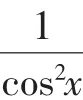
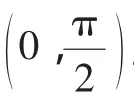
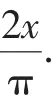
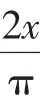
四、取对数后构造函数证明

例4a，b∈R且b＞a＞e，其中e为自然对数的底数.

证明：ab＞ba.

证明：原不等式两边同时取自然对数，可知

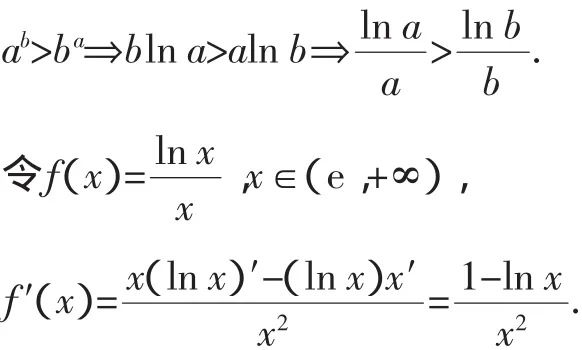
因为x＞e时，f′（x）＜0，所以f（x）在（e，+∞）上单调递减.

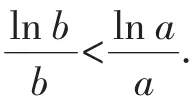
故原不等式成立.

点评：将待证不等式两边同时取对数，转化为合理的辅助函数.

五、从条件特征入手构造函数证明

（1）讨论函数f（x）的单调性；

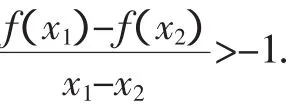
解：（1）f（x）的定义域为（0，+∞），

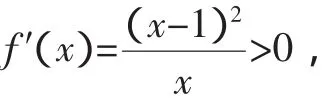
故f（x）在（0，+∞）上单调递增.

（ii）若a-1＜1，而a＞1，故1＜a＜2，则当x∈（a-1，1）时，f′（x）＜0；

当x∈（0，a-1）及x∈（1，+∞）时，f′（x）＞0.

故f（x）在（a-1，1）上单调递减，在（0，a-1）和（1，+∞）上单调递增.

（iii）若a-1＞1，即a＞2，同理可得f（x）在（1，a-1）上单调递减，在（0，1）和（a-1，+∞）上单调递增.

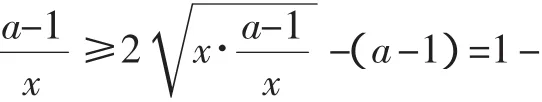
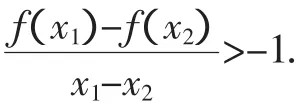
所以原不等式成立.

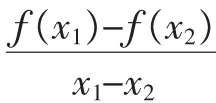
六、换元法后作差构造函数证明

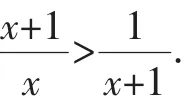
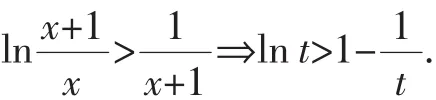
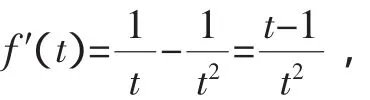
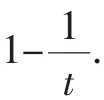
故原不等式成立.

点评：当待证不等式比较复杂时，可以通过换元的方法转化为较熟悉或比较简单的不等式.

七、利用两个函数的最值证明

例7 函数f（x）=-x-ln（-x），x∈［-e，0）.

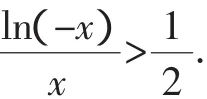
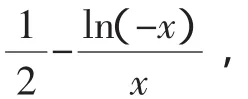
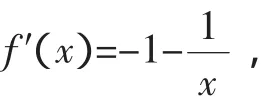
所以当-e≤x＜-1时，f′（x）＜0，此时f（x）单调递减；

当-1＜x＜0时，f′（x）＞0，此时f（x）单调递增，

所以f（x）极小值为f（-1）=1，即f（x）在区间［-e，0）上的最小值为1，所以f（x）＞1.

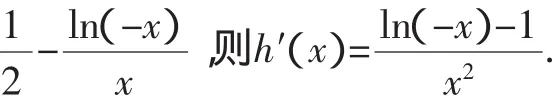
当-e≤x＜0时，h′（x）≤0，故h（x）在[-e，0]上单调递减.

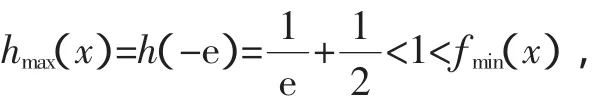
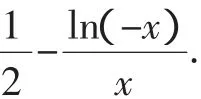
故原不等式成立.

点评：分别转化为两个函数，利用函数h（x）max＜f（x）min进行证明.

近几年来，高考中对函数背景下不等式的考查要求比较高，学生得分情况不容乐观.通过上述几道例题，掌握不等式证明的几个常见技巧，不仅能保证解题的正确性，还能有效地降低试题难度，缩短解题时间.