数列不等式的归纳法证明

☉江苏省丹阳高级中学 章建民

数列不等式在高等数学尤其是在分析数学的极限、级数中有着广泛的应用，因而这类问题在近几年的高考、自主招生考试、数学竞赛中屡见不鲜，成为考试的热点；但是数列不等式的证明经常要用到放缩法，而放缩法需要学生有敏捷的数学观察力和熟练的代数变形能力，同时还要注意恰当的放缩度，技巧性强且难以操控，因而成为学生学习和考试的难点.但数列不等式是与正整数有关的命题，故很自然地可考虑用学生容易掌握的数学归纳法来加以处理，本文采用数学归纳法这一利器来证明数列不等式，供参考.

一、直接应用数学归纳法证明

例1（2012年高考全国大纲卷理科22题）已知函数f（x）=x2-2x-3，定义数列{xn}：x1=2，xn+1是过两点P（4，5），Qn（xn，f（xn））的直线PQn与x轴的交点的横坐标.

（1）证明：2≤xn＜xn+1＜3；

（2）求数列{xn}的通项公式.

证明：（1）过P（4，5），Qn（xn，-2xn-3）两点的直线方程是y-5=（xn+2）（x-4），它与x轴的交点是，所以

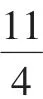
假设n=k时，命题成立，

即2≤xk＜xk+1＜3；

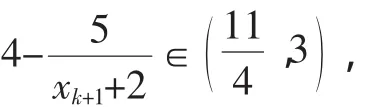
所以2＜xk+1＜xk+2＜3，

即n=k+1时也成立.

综上由数学归纳法可知命题对任意n∈N*都成立

（2）略.

下面可用数学归纳法来证明an＜1.

当n=1时，a1＜1，结论成立；

假设当n=k（k≥1）时，ak＜1.

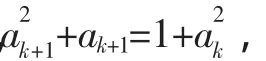
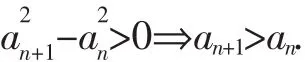
（2）略.

二、利用加强命题法证明原数列不等式

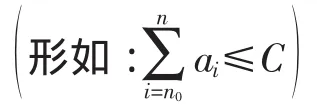
分析：（1）首先假设命题可以强化为：

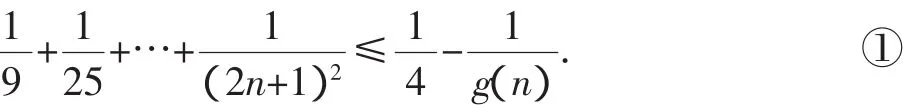
接着思考的问题自然是：要使加强命题成立，g（n）应满足什么条件呢？

（2）既然加强命题①成立，则可以利用数学归纳法加以证明：

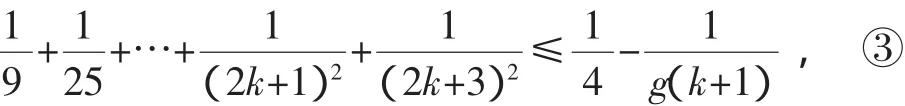
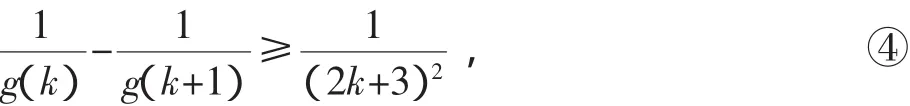
则可以由不等式的传递性知道③式成立，从而由归纳法原理证明了加强命题①.从上述分析可知，g（n）必须同时满足②④两式.

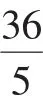
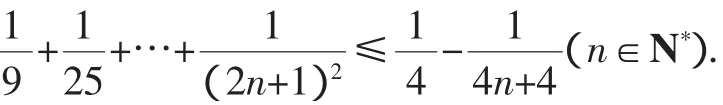
证明：先用数学归纳法证明原不等式的一个加强不等式：

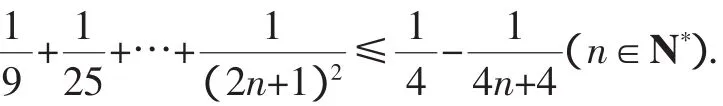
假设当n=k（k≥1）时不等式成立，

当n=k+1时，

加强不等式当n=k+1时也成立，所以加强不等式恒成立.

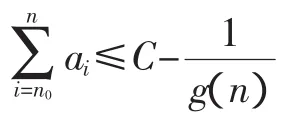
构建加强不等式是证明数列不等式问题的一种有效方法.从不等式的结构形式可分为三类：同侧加强、异侧加强和双向加强，这是利用数学归纳法证题的精髓所在.

1.同侧加强

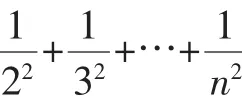
分析：若设n=k时不等式成立，

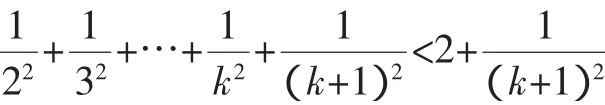
由此在常数的同一侧采用上述加强命题法得出一个加强不等式：

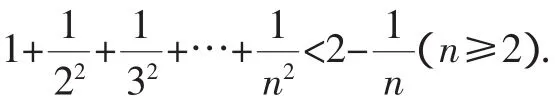
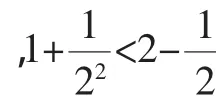
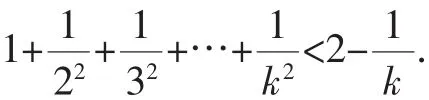
当n=k+1时，

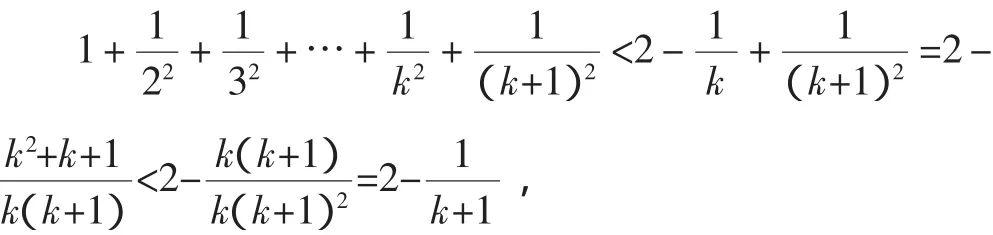
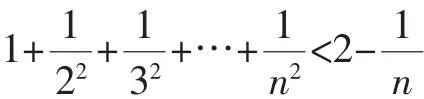
2.异侧加强

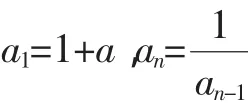
分析：本题直接用数学归纳法无法证得an＞1，对它的另外一侧实施加强得加强不等式：

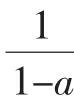
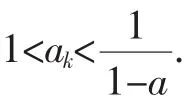
当n=k+1时，一方面，有

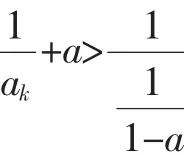
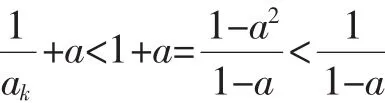
评注：从表面上看，加强命题使原问题变复杂了，而实际上，通过加强命题可以得到一个较强的归纳假设，从而为归纳过渡的顺利完成奠定坚实的基础，反而有利于原问题的解决.另外，这种异侧加强有广泛的适用性.

3.双向加强

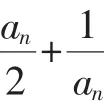
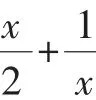
证明：先用数学归纳法证明：对一切正整数，有

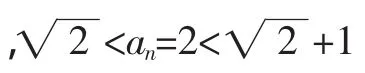
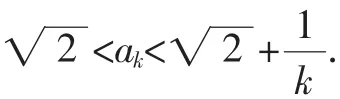
当n=k+1时，一方面，由均值不等式有

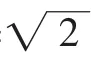
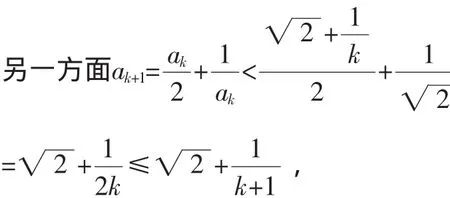
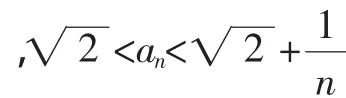
故不等式（＊）成立.

由上可知数学归纳法证明数列不等式可规避传统的不等式放缩来证明数列不等式中灵活多变的方法和高难技巧，解题有明确的指向和固有的定式，思维流畅自然，使很多复杂的数列不等式的证明题迎刃而解，具有较广泛的适用性.这样处理不等式问题既适应新课改的需求（新课程标准已将不等式证明内容纳为理科选修内容），又符合“淡化特殊技巧，注重通性通法”的新高考理念，且能有效提高学生的思维能力和解题能力，促进数学的高效学习，值得在教学和解题训练中加以推广使用.