诠释高考对数学解题能力的考查

☉广东省清远市第一中学 郭智君

解题能力是指能阅读、理解题目所陈述的材料，并对材料所提供的信息进行分析、加工、筛选和处理，选择恰当的方法，综合应用所学数学知识、思想和方法解决问题的能力.它是逻辑思维能力、运算能力、空间想象能力等基本数学能力的综合体现，提升学生的解题能力是数学教学最重要的任务.高考考查的首要任务即是对学生解题能力的考查，下面以2013年高考导数试题为例说明.

一、考查对问题信息收集整理的准确性

一个数学问题，必然会向考生提供该题目的有关信息，包括条件是什么，解题的设问方向是什么等.解答题给予我们的信息量大，如何通过审题抓住有效信息，排除干扰信息，去除无效信息，获得解题的第一感受资料十分重要.

例1 （2013年全国新课标I卷）已知函数f（x）=x2+ax+b，g（x）=ex（cx+d），若曲线y=f（x）和曲线y=g（x）都过点P（0，2），且在点P处有相同的切线y=4x+2.

（Ⅰ）求a、b、c、d的值；

（Ⅱ）若x≥-2时，f（x）≤kg（x），求k的取值范围.

信息收集：（1）两曲线同时过点P（0，2），即两函数在x=0时，函数值相等；题目中涉及曲线在点P（0，2）处的切线相同，即意味着在该点的导数值相等.

信息整理：（2）当x≥-2时，f（x）≤kg（x）恒成立，

即［kg（x）-f（x）］min≥0.

解析：（Ⅰ）由已知得f（0）=2，g（0）=2，f′（0）=4，g′（0）=4.

而f′（x）=2x+a，g′（x）=ex（cx+d+c），所以a=4，b=2，c=2，d=2.

（Ⅱ）由（Ⅰ）知，f（x）=x2+4x+2，g（x）=2ex（x+1），设函数F（x）=kg（x）-f（x）=2kex（x+1）-x2-4x-2（x≥-2），F′（x）=2kex（x+2）-2x-4=2（x+2）（kex-1），由题设可得F（0）≥0，即k≥1.

令F′（x）=0，得x1=-lnk，x2=-2.

若1≤k＜e2，则-2＜x1≤0，所以当x∈（-2，x1）时，F′（x）＜0；当x∈（x1，+∞）时，F′（x）＞0.即F（x）在（-2，x1）上单调递减，在（x1，+∞）上单调递增，故F（x）在x=x1时取最小值F（x1），而F（x1）=2x1+2-x12-4x1-2=-x1（x1+2）≥0，所以当x≥-2时，F（x）≥0，即f（x）≤kg（x）恒成立.

若k=e2，则F′（x）=2e2（x+2）（ex-e-2），所以当x＞-2时，F′（x）＞0，所以F（x）在（-2，+∞）上单调递增，而F（-2）=0，所以当x≥-2时，F（x）≥0，即f（x）≤kg（x）恒成立.

若k＞e2，则F（-2）=-2ke-2（k-e2）＜0，所以当x≥-2时，f（x）≤kg（x）不可能恒成立.

综上所述，k的取值范围为［1，e2］.

点评：解题时应细心阅读问题，全面收集信息，正确地掌握设问的要求.为此考生应始终保持清醒的头脑，注意克服由于思想紧张或思维的片面性而导致收集信息不全、收集信息失真的缺点.

二、考查解决新问题的能力

“新问题”即情景新、题型新、设问新、方法新，教学中一定要认真培养学生解决新问题的能力.解决新问题的能力就是“从无到有”的探索能力和创造意识.要培养学生在陌生的情境下，从题意的挖掘开始，一步一步找到解决问题的途径，学会从不知到知、从不懂到懂、从不会到会、从不明白到明白的“从无到有”的探索方法.

例2（2013年北京卷文）已知f（x）=x2+xsinx+cosx.

（Ⅰ）若曲线y=f（x）在点（a，f（a））处与直线y=b相切，求a与b的值.

（Ⅱ）若曲线y=f（x）与直线y=b有两个不同的交点，求b的取值范围.

解析：（Ⅰ）f′（x）=2x+sinx+xcosx-sinx=x（2+cosx）.

f′（a）=a（2+cosa）=0，所以a=0，b=f（a）=f（0）=1.

（Ⅱ）由f′（x）=x（2+cosx），可知f（x）在（-∞，0）上单调递减，在（0，+∞）上单调递增.fmin（x）=f（0）=1.

若曲线y=f（x）与直线y=b有两个不同的交点，则b≤1不符合题意.

当b＞1时，f（-2b）=f（2b）≥4b2-2b-1>4b-2b-1＞b，所以∃x1∈（-2b，0），x2∈（0，2b），使f（x1）=f（x2）=b，所以b＞1时，曲线y=f（x）与直线y=b有且仅有两个不同交点，所以b∈（1，+∞）.

点评：本题对于实行新课标以来的北京市试题可谓最大创新，一改以往的命题形式，对于解题能力稍差一些的考生来说，便不知从何下手.利用导数研究函数性态的高考数学试题，导数只不过是创设这类试题情境的一种取向，求导的过程并不难，它的最终落脚点是考查函数的性质、不等式的解法、等价转化的思想、分类讨论的思想、数形结合的思想等数学思想方法，特别是体现导数的应用价值，这是需要在复习中强化的关键问题.

三、考查运算的条理性

在数学解题中，有许多问题的运算量比较大，有时也比较繁，但又是不可避免的.在导数问题的处理中，有些问题虽然有好的方法，但在探究中也不容易一下子发现，因此在解题中要提高运算的条理性，如打草稿要一行一行的写，一题一个位置，复查也方便；式子的变化不要跳步，这些都有助于提高我们的运算准确性.

例3（2013年广东理）设函数f（x）=（x-1）ex-kx2（其中k∈R）.

（Ⅰ）当k=1时，求函数f（x）的单调区间；

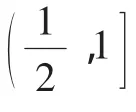
解析：（Ⅰ）当k=1时，

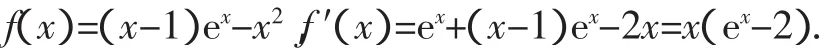
令f′（x）=0，得x1=0，x2=ln 2.

当x变化时，f′（x）、f（x）的变化如下表：

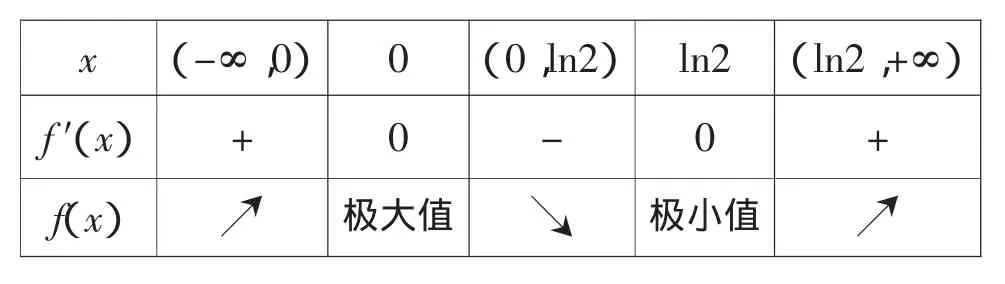
x （-∞，0） 0 （0，ln2） ln2 （ln2，+∞）f′（x）+0-0+f（x）↗极大值↘极小值↗

由表可知，函数f（x）的递减区间为（0，ln 2），递增区间为（-∞，0）和（ln 2，+∞）.

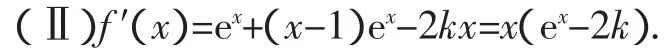
令f′（x）=0，得x1=0，x2=ln（2k）.

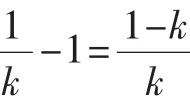
所以g（k）≤ln 2-1=ln 2-ln e＜0，从而ln（2k）＜k，所以ln（2k）∈［0，k］.

所以当x∈（0，ln（2k））时，f′（x）＜0；当x∈（ln（2k），+∞）时，f′（x）＞0.

所以M=max｛f（0），f（k）｝=max｛-1，（k-1）ek-k3｝.

令h（k）=（k-1）ek-k3+1，则h′（k）=k（ek-3k）.

令φ（k）=ek-3k，则φ′（k）=ek-3≤e-3＜0.

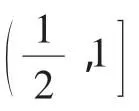
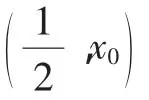
综上，函数f（x）在［0，k］上的最大值M=（k-1）ek-k3.

点评：含参函数单调性的判断问题是高考对导数应用考查的重点内容，解题时注意定义域优先原则，求导后即转化为函数的零点问题.分类讨论思想伴随着导数应用的始终，如根的个数、根的大小等进行分类讨论，另外备考中还需要加强极值、最值问题求解的训练，以及与不等式恒成立问题相结合考查.

四、考查对问题转化的能力

函数的零点个数，即是图像与x轴的交点个数，而有些函数非常复杂，要快速画出函数的图像相对来说比较困难，这时，我们可以借助导数，探究函数的单调性和极值，从而画出函数的大致走势，确定函数的零点个数.

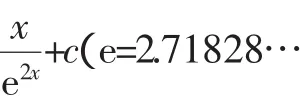
（Ⅰ）求f（x）的单调区间、最大值；

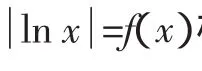
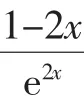
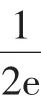
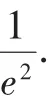
点评：同一个数学问题，由于观察的角度不同，对问题的分析、理解的层次不同，可以导致转化目标的不同与方法的不同.借助于这一特点，可以从尽量简单、显性、容易、明了、一般、具体着手，以更好地解决问题，培养解决问题的能力，优化思维品质.

五、考查求解交汇问题的能力

导数作为新增加的知识，其作用日趋明显，已成为解决许多具体问题必不可少的工具.近几年高考对导数与不等式的整合应用，有加大的趋势.

例5（2013年高考天津理）已知函数f（x）=x2lnx.

（Ⅰ）求函数f（x）的单调区间；

（Ⅱ）证明：对任意的t＞0，存在唯一的s，使t=f（s）；

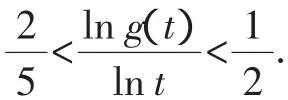
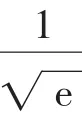
x 0， 1（）1 1■e ，+∞■e （ ）■e f′（x）-0+f（x）↘极小值↗

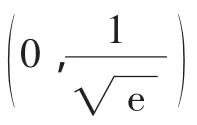
（Ⅱ）证明：当0＜x≤1时，f（x）≤0.设t＞0，令h（x）=f（x）-t，x∈［1，+∞）.由（Ⅰ）知，h（x）在区间（1，+∞）上单调递增，h（1）=-t＜0，h（et）=e2tln et-t=t（e2t-1）＞0，故存在唯一的s∈（1，+∞），使得t=f（s）成立.

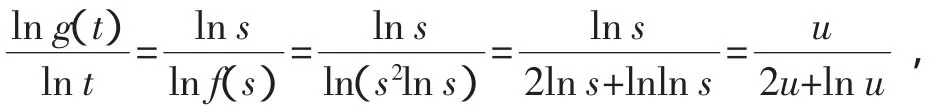
当t＞e2时，若s=g（t）≤e，则由f（s）的单调性，有t=f（s）≤f（e）=e2，矛盾，所以s＞e，即u＞1，从而lnu＞0成立.

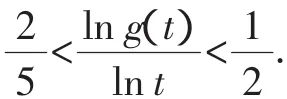
点评：将所要证的不等式通过构造函数的方法，利用求导的思路使问题得到证明，导数为证明不等式问题开辟了新方法，使过去不等式的证明方法从特殊技巧变为通解通法，符合高考命题的指导思想.