对一道自主招生不等式试题的进一步研究

☉上海市松江二中 卫福山

2008年南京大学自主招生不等式试题如下：

问题：设a，b，c∈R+且a+b+c=1，求证：

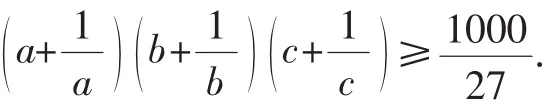
对于以上问题，文［1］给出了三种证明方法，主要用到函数的凸凹性及均值不等式，文［2］指出文［1］的三种证明方法都属于“超纲”方法，并给出了一种不超纲的初等方法.特别地，文［2］给出了以上问题推广的三个命题：

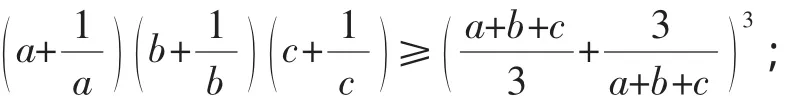
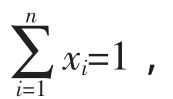
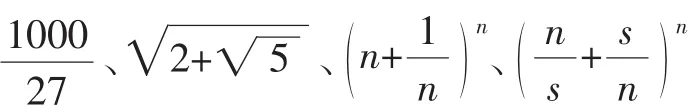
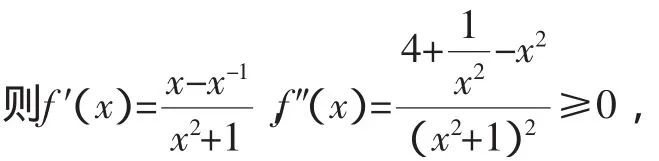
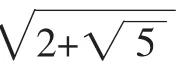
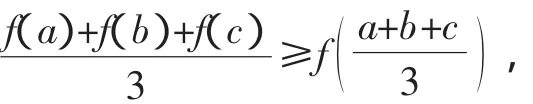
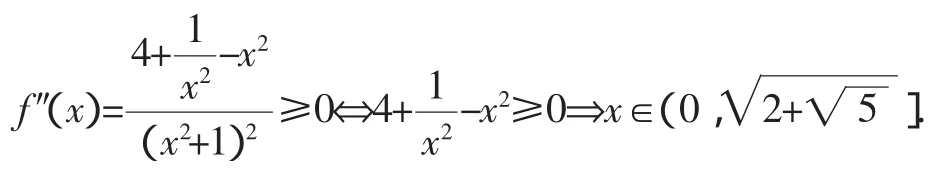
读者对于命题2、3可采用类似的角度去理解，因此问题及三个命题实际上也可以认为是函数的凸凹性及Jesen不等式在具体函数上的应用而已.顺着这样的思路下去，我们可以提出很多貌似新颖的问题.

角度1：问题中字母a，b，c轮换能得到什么不等式？

问题1：设a，b，c∈R+且a+b+c=1，

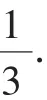
角度2：将问题1从系数上加以推广

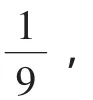
（参见文［3］定理1）

分析：在文［3］中杨学枝老师利用赫尔德（Holder）不等式给出了问题2的证明，实际上问题2只是在系数上对问题1加以推广，证明方法完全类似.

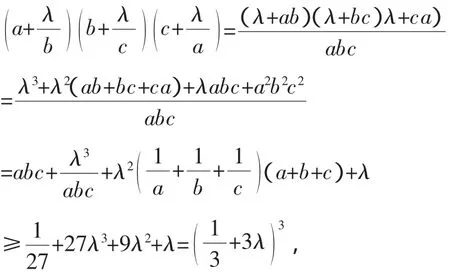
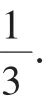
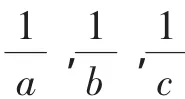
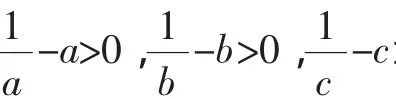
问题3：设a，b，c∈R+且a+b+c=1，

分析：以上不等式的证明可以在很多文献中找到，如文［4］～［7］，其证明方法有五种，下面给出其中用凸凹性的较简单的证明.

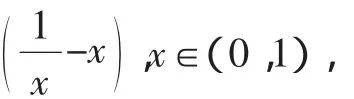
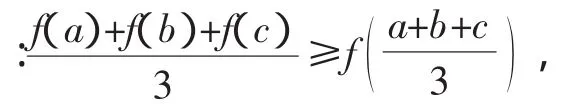
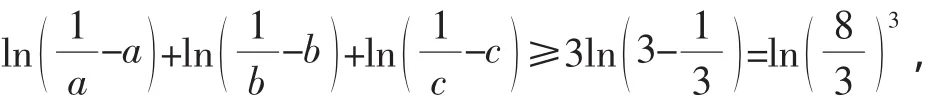
去掉对数符号即得证.

角度4：将问题3中字母a，b，c轮换能得到什么不等式？

问题4：设a，b，c∈R+且a+b+c=1，

证明：对于a，b，c∈R+，有如下几个常用不等式：

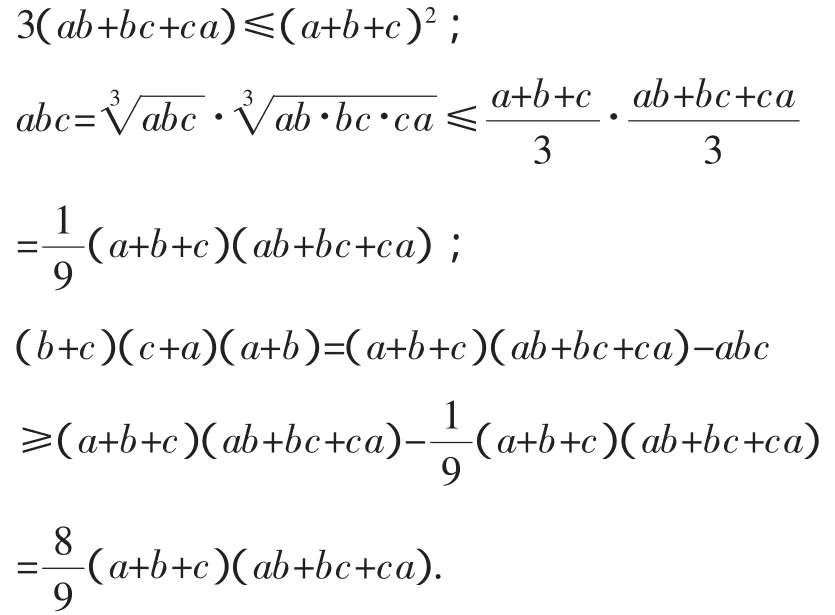
在以上不等式及条件a+b+c=1下，有

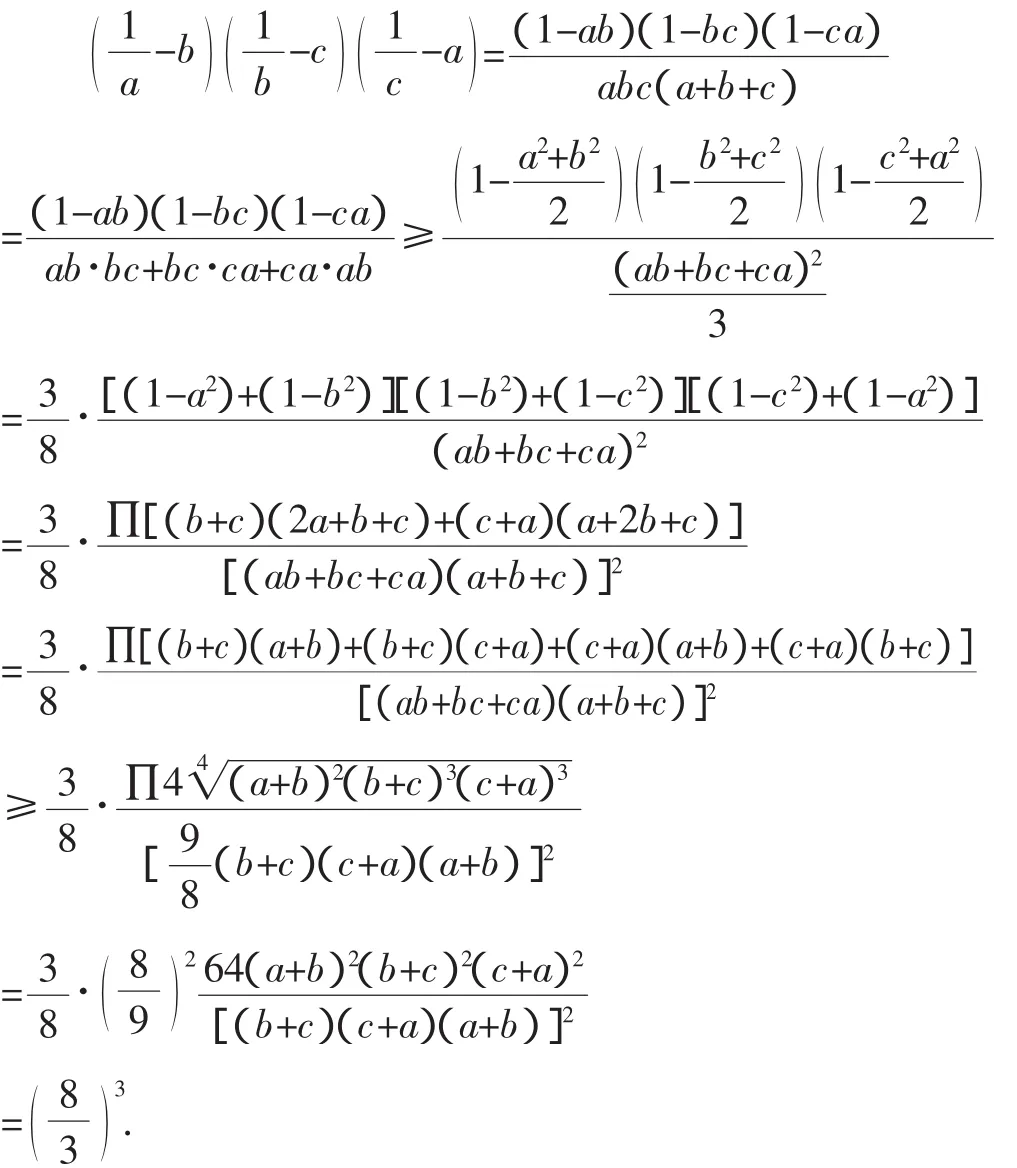
读者可以在问题4的基础上继续研究，如研究其各种形式的推广等，这里从略.

角度5：将条件“a+b+c=1”改成“abc=1”，有哪些结论？

问题5：设a，b，c∈R+且abc=1，

问题4稍加变化，便得到2007年乌克兰数学竞赛不等式试题：

设a，b，c∈R+且abc≥1，

关于其证明，读者可以参阅文献［8］.

问题6：设a，b，c∈R+且abc=1，

读者可以将研究继续进行下去，从中我们或许能产生很多新颖的不等式.

1.时宝军，李淑莲，于瑞广.一道自主招生数学试题的解法探究与评析［J］.数学通讯（下半月），2010（2）：56-57.

2.赵思林，李兴贵.一道自主招生不等式试题的初等解法探究［J］.数学通讯（下半月），2010（10）：49.

3.杨学枝.两个代数不等式猜想的推广［J］.数学通讯（下半月），2010（10）：38-39.

4.杨先义.一个不等式的推广［J］.数学通讯，2002（19）：29.

5.梁丽平，安振平.一个代数不等式的两种初等证法［J］.中学数学研究，2003（3）：41-42.

6.马占山，薛卫华.一个不等式的简单初等证明［J］.数学通讯（下半月），2010（5）：33.

7.李歆.也谈一个不等式的简单初等证明［J］.数学通讯（下半月），2010（9）：29.

8.邹守文.一道2007年乌克兰竞赛题的简证［J］.中学数学，2007（8）：25.