三次函数在“导数”教学中的价值分析
☉江苏省镇江市国际学校 宋仁高
任何一种教学,最低目标是通过一系列的教学进程,使学习者获得某种知识与技能的发展;当然在获得知识与技能的基础上,获得思维启迪、思想跃升与综合素质提高进而改变哲学观,这是最高层级目标.新课标提出高中数学教学的三维教学目标,为实现这些目标,教师在教学设计过程中,往往从浩瀚数学之海中掬一杯清澈涓流,精心运用于教学过程;多年实践证明,课堂教学素材的选取是否合适、运用是否得当往往影响教学效果.以“导数”教学为例,笔者发现选取“三次函数”素材作为教学“导数的运用”十分合适,精心设计问题,积极引导学生对“三次函数”的若干性质进行探究,则可很好地落实“导数”教学的三维目标,下面从两个方面浅析这一过程.
一、借心理学理论“最近能力发展区”原理,凸显三次函数的性质探究在导数教学中的价值
教育心理学认为,处于学生最近能力发展区的教学内容,是最合适的教学内容.从现有数学教育体制看,“导数”学习,对学生数学处于“承上启下”的地位:初中数学开始接触函数,意味着由小学开始学习的“常量”为主的数学开始进入中学阶段的“变量”为主的数学,高一接触了关于初等函数的几个特征,如定义域、值域、奇偶性、对称性、增减性、周期性等.这正是进入高二之后学习“导数”的基础;高二学习导数,是对前者的深化,是站在更高的视角,是运用更为深入的、更为本质的概念推进函数的探究与学习,“导数”体现了现代数学的思想,即通过对数学对象的某种特征的探究进而了解该对象的性质.高二数学导数教学要体现这一思想,为学生进入大学学习现代数学打下基础,而不仅仅是让学生知道几个定义、记住几个公式、机械地套用公式进行计算等.
回溯高二数学教学背景可看出,基本初等函数特别是二次函数的学习是高二学生学习导数的能力基础,二次函数与一元二次方程、一元二次不等式三位一体、紧密相关,从函数图像、函数性质到方程求解、根的分布、不等式的解集区间分布等,知识与能力要求环环相扣,集中体现了数学的理解能力、推理能力、想象能力、几何作图能力、运算能力等.二次函数是学生在学习导数前了解最多、运用最娴熟的数学对象,二次函数学习中习得的函数研究的一般步骤与思路,为学习、运用导数研究函数性质及相关问题奠定了方法与知识基础.三次函数无论从函数的代数特征、图像的几何特征还是函数性质的研究、推理手段等来看,与二次函数最为相近,但是,量变引起质变的哲学辩证思维启发我们,从二次函数到三次函数,并非是简单的函数因变量的指数变化,三次函数毕竟具有二次函数所没有的诸多特点,与之俱来的若干问题也不是仅能照搬二次函数的研究方法解决的.从三个维度的教学目标看,三次函数正是处于高二阶段学生的最近数学能力发展区的数学学习素材.下面通过一道典型的试题的剖析加以说明如何以三次函数为素材进行导数教学.
例1设有函数f(x)=x3-3ax2+3x+1.(1)设a=2,求f(x)的单调区间;(2)设f(x)在区间(2,3)中至少有一个极值点,求a的取值范围.
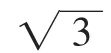
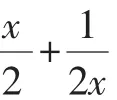
点评:在解决第一问时,通过求导,将三次函数的增减性讨论转化为一元二次方程的求根与一元二次不等式的求解问题,求导的解题功能体现为将三次函数直接转化为二次问题,而转化后问题中不含参数讨论,比较简单,体现数学解决问题的特点,即不断将未知问题转化为熟悉问题解决;解决第二问,导数起到的作用仍然是将三次问题转化为二次函数,但转化后得到的二次问题含有参数,如果仍拘泥于求出含有参数的方程解,接着利用不等式结合解所在区间求解,将相当繁琐,反过来将参数视为原来自变量x的函数,将求参量变化区间问题转化为讨论一个新函数的值域问题,此时讨论值域问题无需求导,应灵活地根据解的代数表达式及自变量变化区间,将问题直接转化为基本不等式处理的问题.本题中,“求导”作为问题转化的技术手段,所需思路是在原有数学基础上“跳一跳,够得到”.
二、视三次函数为载体,配合导数处理更加复杂的数学问题,体现“工具”特点的价值所在
在数学学习中,不断提出新问题与解决新问题的尝试往往能有效检验已经学过的数学知识与方法,检验已经了解的数学思想理解的深度,进而促进知识与方法的掌握,这在数学家波利亚的《怎样解题》一书中有精彩的描述.经过基础性内容与方法的学习和训练之后,教学过程就应该向较高要求过渡,能力发展向多种指标提高的方向努力.运用导数处理三次函数,学生如果掌握的较理想,完全可以将三次函数作为新过渡工具,用导数处理涉及四次函数的问题以及超越函数的问题.这时,三次函数问题讨论的经历与解决问题的解题经验已经成为新的基础.试看下列这道典型四次函数问题:
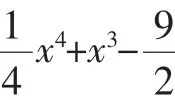
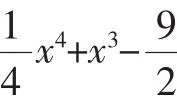
g(x)=x3+3x2-9x的两个极值点为x1=-3和x2=1,一个极大值为g(-3)=27,一个极小值为g(1)=-5,粗略画出三次曲线g(x)=x3+3x2-9x的图像如图,当且仅当-27<c<5,g(x)=x3+3x2-9x与h(x)=-c才会恰好有三个交点,问题得证;
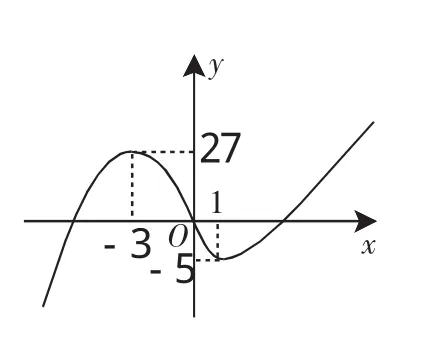
(2)函数f(x)在区间[a,a+2]上单调递减,意味着导函数:
f′(x)=x3+3x2-9x+c在区间[a,a+2]上恒负,此处“存在c”,不能理解成“任意c”,与第一问类似,三次问题“f′(x)=x3+3x2-9x+c在区间[a,a+2]上恒负”,只有通过再次求导转化为二次函数中零点的分布问题讨论,进而得出参数c范围.
点评:数学魅力在于不断在最新的最近发展区中,通过新问题磨练思维、活化思维,学会数学知识、数学方法的迁移应用,达到真正领会相应的数学思想,进而有效提高数学水平.此题第一问培养学生如何根据三次函数图像解决问题的能力,是在运用二次函数抛物线图像的基础上对于数学能力的又一次提高;第二问引导学生,将四次函数问题通过求导,在形式上转化为仍然是“已知自变量x的变化区间,反过来求解参数的变化范围”问题,只不过将例1的第二问问题背景由二次问题换为三次问题,解决的思路是再次求导,将三次问题中参数讨论最终转化为二次问题中的参数讨论.这里,隐藏着将来在高等数学中二阶导数的数学思想,为学生将来的数学能力发展打下基础.问题二比问题一无论在运用知识的广度与深度,还是思维能力的要求方面,都有明显提升,数学问题的曲折会锻炼思维,已经积累的数学学习经验会为终身发展埋下伏笔.
总之,从以上讨论中可见,三次函数对于导数教学具有极高的数学教学价值与数学教育意义,重视并挖掘这一教学素材,是高中数学教师值得重视的问题.

