洞悉误因 对症下药——一道易错题思维误区的调查与分析

☉江苏省华罗庚中学 席国金

一、问题的提出

一道好的练习题可以反映出学生在知识理解上的不足以及思维上的误区.只要发现学生的问题，我们对症下药，就能做到有的放矢.更好的研究学情，可使我们平时命题工作更有针对性，提高命题的质量，以至为我们今后的教育教学工作提供正确的向导.笔者对一道组合问题进行了调查研究，发现了学生容易走入的几个思维误区，进而反思我们课堂教学中的不足与缺陷，并提出一些改进措施.

二、研究过程

1.调查对象

江苏省华罗庚中学的120名在校高二理科学生.

2.调查方法

采用试卷调查法和访谈法.收集试卷115份，选择其中20名学生进行访谈.

三、研究结果与分析

1.试题呈现

题目 把8个相同的球放入4个不同的盒子，有多少种不同放法？

本题是相同元素的分配问题，是关于组合知识应用的一道经典问题，也是隔板法的应用模型.考查化归转化、分类讨论的数学思想，着力于考察学生的综合应用能力.

本题的正确率并不高，只有10%的同学解得答案，还有4.1%的学生没有解答，可能是由于思维受阻或是根本就没有认真做导致的.

2.误区分析

经过统计发现，主要有以下几个思维的误区，误区类型调查结果如下表.

从表中可以看出，学生对此问题的解答错误率很高，对此我们分析学生走入思维误区的原因.

误区类型 误区1 误区2 误区3百分比 19.1% 50.3% 16.5%

误区1：错误的看成是不同元素的分组、分配问题而致错

19.1%的学生错误地将问题看作是不同元素的分组、分配问题而导致问题的错误解答，主要原因：一是由于学生根本没有理解不同元素的分组、分配问题和相同元素的分组、分配问题，对二者不能够区分而混为一谈；二是由于审题不清，粗枝大叶所致.

误区2：错误的看成是原始问题而致错

原始问题：将n个相同元素放入m（m≤n）个不同的盒子中，每个盒子中至少放一个元素，共有C种放法.

误区3：分类不全面而致错

3.问题分析

从学生的解答来看，做对的学生都是应用了求方程非负整数解的问题模型，将上述问题等效为：求x1+x2+x3+x4=8的非负整数解的组数.

解法1：用a1，a2，a3，a4中ai=xi+1（i=1，2，3，4）（ai为正整数）做代换，有

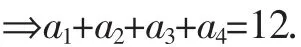
进而转化为求a的正整数解的组数，由隔板法知，有组解.

从本解法来看，这些学生对隔板法已经熟练掌握，不但明确隔板法适用的范围，而且还能类比非负整数解解决此问题.当然这些学生不但基础好，而且学习习惯也好，在学习中能够自主探究和归纳总结.

解法2：对上述误区3的学生的解法进行分析和完善，我们就对x1+x2+x3+x4=8的非负整数解的组数展开讨论即可.对此问题解的情况可以分为4类：

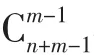
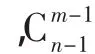
因此，我们就得到了下面的结论：

解法3：（不尽相异元素的全排列的应用）求x1+x2+x3+x4=8的非负整数解的组数，由上可知，就是求a1+a2+a3+a4=12的正整数解的组数.根据解情况分类：

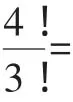
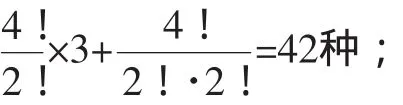
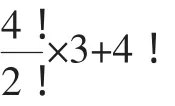
④（2～2～2～6、2～2～3～5、2～2～4～4、2～3～3～4）有

⑤（3～3～3～3）有1种.

综上可知，x1+x2+x3+x4=8的正整数解的组数为165=.

解法1应用了化归转化的数学思想，将原问题转化为非负整数解的问题，再应用隔板法优化了思维过程；解法2、解法3不但应用了化归转化的数学思想，而且应用了分类讨论的数学思想，分类要做到不重不漏，才能走出思维的误区，达到正确解题的目的.通过方法2的探究，我们还得到上述一个结论.

四、结论与建议

1.结论

通过调查，笔者发现学生的思维误区最多的是缺少同类问题概念的辨析、审题不清、偷换概念等带来的误区；其次是知识本身不理解而走入的误区，对于高中生来说，数学思维能力是有限的，而数学思维能力的培养是一项工程.相对而言，考虑问题不全面而带来的思维误区就少了，主要是因为本题难度较大，数学能力的要求很高所致，这也说明学生综合应用知识的能力有限，对于数学思想方法的掌握欠佳.

2.建议

（1）加强概念性教学

为防止学生出现偷换概念而走入思维误区，教学中必须认真备课钻研教材，加强概念性教学，对概念进行辨析、归类，对方法进行总结及模型化，使学生牢固的掌握基本概念、正确运用方法等.

（2）重视数学能力的发展

高考以能力立意，全面考查体现数学学科特点的七个能力，即空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力、数学建模能力、创新意识.良好的思维能力是需要经过多次反复从实践中锻炼出来的.这样通过发散思维训练，突破了固定的思维模式，提高了思维的灵活性.

（3）注重数学思想方法的渗透

高中阶段主要掌握七大数学思想方法，即函数与方程的数学思想、数形结合的数学思想、分类与整合的数学思想、化归与转化的数学思想、特殊与一般的数学思想、有限与无限的数学思想、或然与必然的数学思想，其中在高考中，函数与方程的数学思想方法、数形结合的数学思想方法、化归与转化的数学思想方法体现得最为突出．因此，在平时的教学中要注重渗透数学思想方法，从而优化解题思路，找到合理的突破口，减少解题思维误区的发生.

（4）用正确的方法纠错

认真分析思维误区的形成，针对不同的思维误区，进行易错题归类、总结成题集，以便于学生对知识的再认识.

（5）培养良好的非智力因素

学生的许多思维误区与非智力因素也是离不开的，应在纠正不良的心理品质上下功夫.如：要求学生上课时注意力要集中；要有克服困难的精神，不能知难而退；克服马虎、粗心、不认真检查的毛病；并教育学生树立学习的信心，有助于提高成绩.

1.王振平.中学生数学学习方式的调查分析［J］.数学教育学报，2012（1）.

2.罗增儒.怎样解答高考数学题［M］.陕西师大出版社，1997年3月出版.

3.徐群飞，李俊.中小学生估算意识及策略的调查研究［J］.数学教育学报，2006（3）.

4.涂荣豹.新编数学教学论［J］.华东师范大学出版社.2008年2月出版.