基于数学建模思想的中考题解题策略研究

☉江苏省如东县实验中学 茅玲玲

应用题历来是数学教学的有机组成部分，而很多应用题已经突破了简单应用题的限制，把数学建模的思想应用到其中，比如在设置特定的条件下建立函数不等式，运用函数图像建立解决问题的数学模型.在运用数学知识解决实际问题的过程中，学生既复习了基础数学知识，练习了基本数学方法，同时受到基本数学思想重要性的直观感受和熏陶；更为重要的是数学应用题背景丰富，紧扣生活，条件呈现方式多样，文字、图形、图表、图像及照片都是可能的方式，问题呈现多样化.因此，数学应用题在初中数学教学中成为极其重要的一类教学素材.如何最大限度地发挥数学应用题的数学教育价值？颇值得深思.就其中两类数学建模题，笔者做以下的解题策略归纳与分析：

一、对在限制条件下一元一次函数模型构建，引导学生掌握简单一元一次函数的条件设置，即“函数不等式的数学思想”

纵观近年来全国各地的中考数学试题我们不难发现一类“决策型”应用题出现的频率有所上升，决策型应用题和传统的“行程问题”、“工程问题”有着较大的区别，在实际问题的背景上，由原来局限于确定的数值之间的关系变为更多地涉及变量之间的函数关系，涉及的函数多为一次函数，而函数参与的数量关系不再局限于等量关系，更多地涉及不等关系.因此，针对在特定限制条件下如何进行一次函数的数学模型构建问题，教师在课堂教学中必须引导学生掌握涉及一次函数的不等关系中条件设置的技巧，领悟函数不等式的数学思想.在综合运用不等式和函数的数学思想进行合理推理的基础上，紧密结合题目的现实条件和问题背景，进行“决策分析”，给出问题需要的求解结果.

例1 为了迎接湿地生态旅游节，某市需要对景区附近环境进行布置，市绿化部门研究用培育的3490盆十字花科开红花的植物和2950盆开蓝绿色花的植物配起来组成M型和W型两种花卉造型，总共需要50套.已知构成一个M型需要开红花的植物80盆，开蓝绿色花的植物40盆；构成一个W型需要开红花的植物50盆，开蓝绿色花的植物90盆.

（1）某大学生园艺实习小组承担了这项花卉造型设计与搭配方案的研究任务.那么，你能帮助他们计算一下，符合要求的搭配方案有多少种？将这些方案一一列举出来.

（2）如果组成M型花卉造型，耗费资金是800元，搭配一个W型花卉造型，耗费资金是960元.那么，在问题（1）中哪种设计方案所耗费的资金最少？

解析：（1）假设组成M型花卉造型x个，组成W型花卉造型（50-x）个，根据题意可以得到：80x+50（50-x）≤3490和40x+90（50-x）≤2950，解之得31≤x≤33，则x可取31、32、33.故可以搭配三种方案：①M型花卉造型31盆，W型花卉造型19盆；②M型花卉造型32盆，W型花卉造型18盆；③M型花卉造型33盆，W型花卉造型17盆.

（2）根据题中决策的限制条件，在已知的可供选择的方案中，选出最佳方案.本题可以从两个不同途径思考：①运用列举法筛选决策，分别计算三种方案耗费资金量，第一种31×800+19×960=43040元；第二种32×800+18×960=42880元；第三种33×800+17×960=42720元；则第三种方案耗费的资金最少.②运用推理进行决策，比较不同方案，发现W型花卉造型耗费的资金比M型花卉造型耗费的资金多，则W型花卉造型越少，总的耗费的资金就越少，故第三种方案所需的资金最少.

点评：本题是一道典型的通过构建一次函数模型进行解决决策型问题，大部分学生都仍习惯于列方程组解决问题，而此题中提供的开红花和开蓝绿色花的植物数量并非恰好构成50套花卉造型，而是确保“能够”，因此花卉植物的盆数可能有余，所以应该指导学生理清本题中出现的一次函数，而涉及一次函数的的数量关系不是等量关系，而是不等关系，应该从经典的列方程组方法转为运用函数不等式表达已知条件.

二、函数图像型模型构建问题，引导学生从注重“数量关系”的代数化向图形化进行转变，并能读懂函数图像的内涵，即函数中点、线、面积的含义

图像型应用题在近年来的中考数学试题中也是屡见不鲜，这类试题一改以往以语言及数学表达式的形式交代已知条件、所求问题的命题风格，而是通过图像呈现问题涉及的条件，要求学生在研读、判断图像的基础上展开思路.教师要引导学生将思路从注重纯粹“数量关系”转移到“数图结合”，培养学生良好的读图习惯，注意到题目所给的平面直角坐标系中纵横坐标轴的实际意义，观察图像的变化趋势，如图像的拐点、交点等特征，尤其要挖掘图像与x、y轴交点的意义.除此之外，还应引导学生要紧密结合生活经验和邻近学科知识，如物理定律等，不能从纯粹数学函数图像的视角看待问题中呈现的图像.

例2 某旅游景区由于此前一段时间天气干旱，景区中的A湖泊因临时清淤以及向周围的几个社区供水，导致其蓄水量每天以相同速度持续减少，管理部门决定从B湖泊以管道向A湖泊输送水，图1为两座湖泊的蓄水量与时间之间的函数关系图像.假设相同时间内B湖泊的输出水量与A湖泊的输入水量相等，此外假设在输运过程中由于采用管道输送，水的损耗量很小可以忽略不计.试求：

（1）B湖泊每天的放水量是多少万立方米？

（2）在第几天时，B湖泊管道输出的水开始进入A湖泊？此时A湖泊的蓄水量为多少万立方米？

（3）求图像中直线QS的函数表达式.

解析：（1）由图1可知：t=0～5这5天中，B湖泊每天输出水量是（3000-1000）÷5=400万立方米.

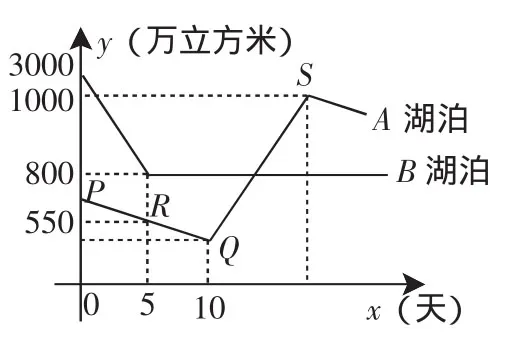
图1

（2）t=0～10这10天中，A湖泊的水量一直在减少，但从t=10天开始A湖泊的蓄水量与实际函数关系图像纵坐标开始增加，说明A湖泊在第十天蓄水量才开始增加，此时也是B湖泊的水开始输入A湖泊中；令直线PQ的一次函数表达式为y=kx+b，将P（0，800）、R（5，550）代入得到：b=800，k=-50，即y=-50x+800，将x=10代入可得到第10天来自B湖泊的水开始输入A湖泊时A湖泊内的蓄水量为y=300万立方米.

（3）此问中相当多的学生因为S点的坐标求不出来而放弃求解，这里教师该引导学生注意到S点坐标只有联系问题的实际背景求解，抓住题中“假设相同时间内B湖泊的输出水量与A湖泊的输入水量相等，此外假设在输运过程中由于采用管道输送，水的损耗量很小可以忽略不计”，不难看出，A湖泊输入的水量等于B湖泊输出的水量，即2000万立方米，A湖泊输入水用的时间等于B湖泊输出水的时间即5天，而15天后A湖泊的蓄水量为（3000-1000）+300-50×5=2050万立方米.将S（15，2050），Q（10，300）代入一次函数表达式y=k1x+b1，可得k1=350，b1=-3200，则QS的函数表达式为y=350x-3200.

点评：相当多的学生在解决图像型问题时，要么抛开图像，执着于从题目的文字叙述与数字中寻求解答，要么离开题目的背景看待题中呈现的图像.其实在这道典型的图像题中，为了求出S的坐标，就必须联系题目中交代的“假设相同时间内B湖泊的输出水量与A湖泊的输入水量相等，此外假设在输运过程中由于采用管道输送，水的损耗量很小可以忽略不计”.这实际上隐含了“B湖泊的输出的时长等于A湖泊的输入时长”.在这道题中，还有相当一部分学生误求了S点的纵坐标为yS=（3000-1000）+300=2300，这是因为他们没有注意到在B湖泊向A湖泊输入水时，A湖泊同时仍在向周围几个社区供水.

通过以上两类数学建模问题可见，应用题教学要指导学生摆脱过于依赖纯粹数量关系解题的习惯，教师要从解题的思路与数学思想运用的介绍上着手，培养学生良好的联系生活实际、联系问题背景解决数学应用题的习惯，才能真正落实新课标高效率、高效益数学教学的理念.