利用多星矢量观测信息进行天文导航定位技术的研究

李崇辉，李铸洋，郑 勇，张 超

（信息工程大学 导航与空天目标工程学院，郑州 450001）

1 引言

传统的天文导航定位原理都是基于天文定位三角形或高度差法来实现的，其显著特点是以小视场光学成像系统为核心部件，由于观测效率低下，所以每次进行导航定位时一般只能利用2－3个天体的观测信息。然而要实现快速高精度的天文导航定位，就需要同时观测多个天体的信息，并利用处理设备实时解算得到测站的位置［1-6］。目前大视场天文导航设备的出现使得人们能够同时获得多个天体的观测信息，但是常用的导航定位方法还是传统的定位三角形原理［7-9］，本文提出了一种基于矢量分析的，可以同时处理多星观测信息的天文导航定位方法。其基本过程是确定观测天体分别在地心赤道坐标系和地平坐标系中的位置矢量，并据此求得两坐标系之间的转换矩阵，根据该转换矩阵即可求得测者的位置信息。

2 相关坐标系统及转换

天文导航定位涉及多个坐标系统，如用于表示天体视位置的地心赤道坐标系，用于表示天体地平位置的地平坐标系，以及固连于观测仪器的载体坐标系。为方便起见，假设天文观测时载体精确水平，并且其航向指向正南，即载体坐标系与地平坐标系重合。

2.1 地心赤道坐标系

地心赤道坐标系的坐标原点位于地心，其X轴指向春分点，Y轴指向上点，Z轴指向北天极，X轴、Y轴和Z轴构成右手系。通常用赤经α和赤纬δ来表示天体在地心赤道坐标系中的坐标［10］，如图1所示。

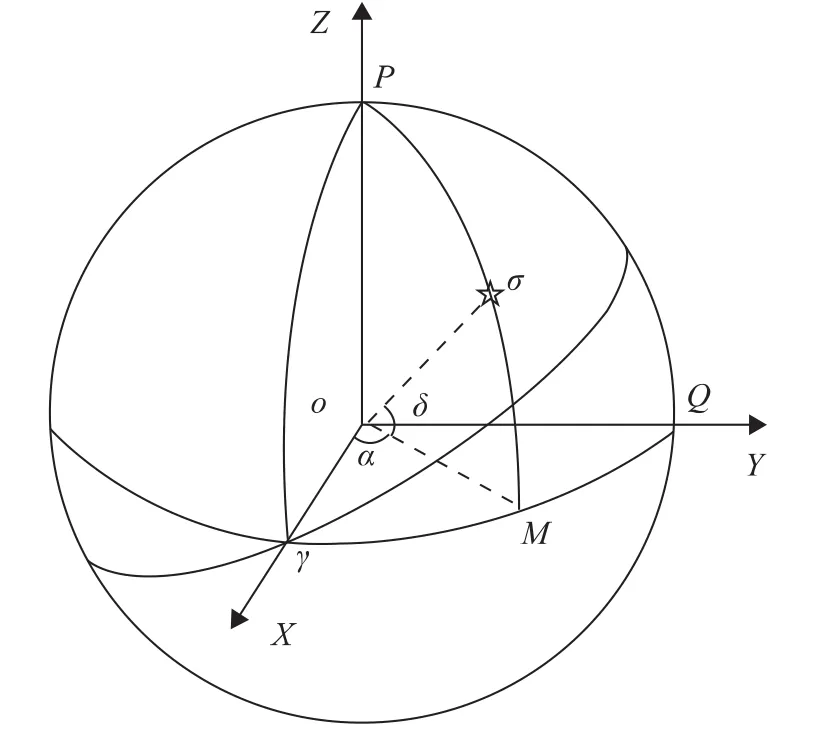
图1 地心赤道坐标系

根据观测时刻，从星表中可直接推算得到的天体的地心赤道坐标 （视位置），一般都表示为赤经和赤纬 （α，δ），也可用空间直角坐标表示为

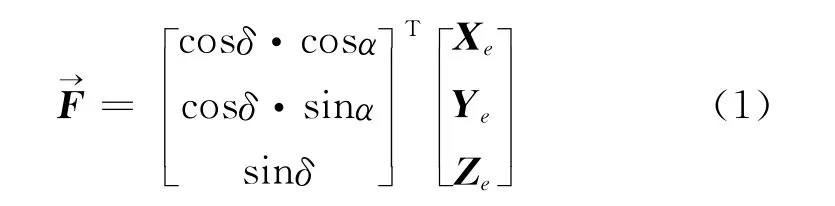
式中

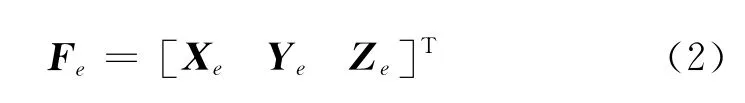
式中，Fe为地心赤道坐标系的单位坐标基，Xe、Ye、Ze分别为三个坐标轴方向上的单位矢量。

2.2 地平坐标系

地平坐标系的坐标原点位于测站中心，其X轴指向正南方向，Y轴指向正西方向，Z轴指向天顶，X轴、Y轴和Z轴构成左手系。通常用方位角A和高度角h来表示天体的地平坐标［9］，如图2所示。

若观测载体精确水平，并且天文观测仪器的零轴指向正南方向，则可直接观测得到天体的地平坐标 （A，h），也可用空间直角坐标表示为

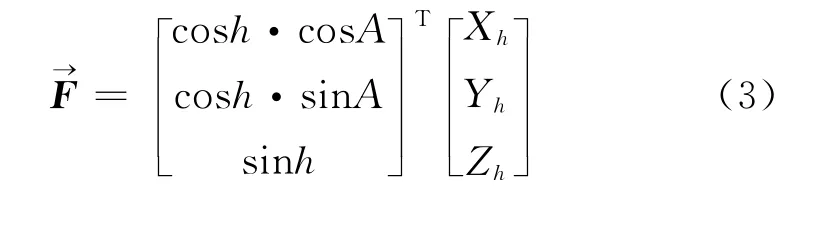
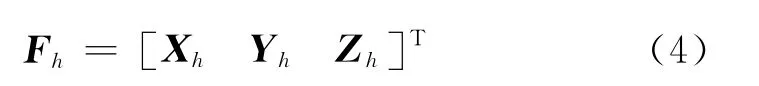
式中，Fh为地平坐标系的单位坐标基，Xh、Yh、Zh分别为三个坐标轴方向上的单位矢量。

2.3 坐标系之间的转换

地平坐标系到地心赤道坐标系之间的转换需要以时角坐标系Ft为中介，其定义可参阅文献［9］。若测站经纬度为 （λ，φ），首先以Y轴为旋转轴，将地平坐标系系旋转一个ψ角

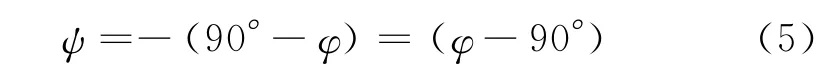
使地平坐标系的Z轴与时角坐标系的Z轴重合。则可得转换关系式为

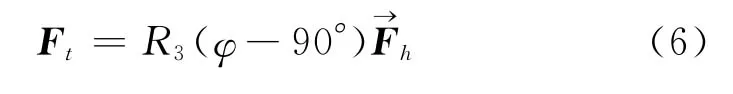
然后从时角坐标系转换到地心赤道坐标系，注意到地平坐标系和时角坐标系均为左手系，而地心赤道坐标系为右手系，因此转换前应先将Y轴反向，并以Z轴为旋转轴，将时角系旋转一个θ角：

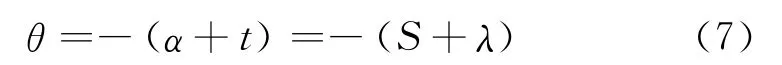
式中，S为观测时刻的格林尼治恒星时，可由观测时的协调世界时时刻换算得到［10］。旋转后使时角坐标系的X轴与重合地心赤道坐标系的X轴重合，则可得转换关系式为

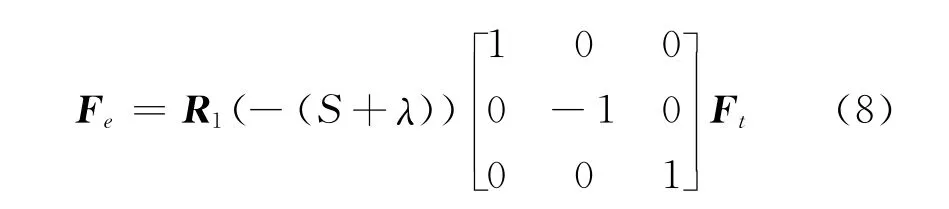
综合式 （6）及式 （8）可得地平坐标系到地心赤道坐标系之间的转换关系为

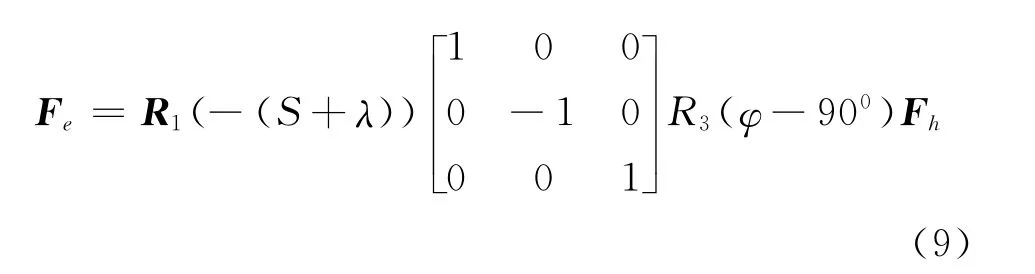
从式 （9）中可以看出，地平坐标系到地心赤道坐标系之间的转换矩阵只包含了测站的经度λ和纬度φ两个未知参数。因此，只需要求得两坐标系之间的转换矩阵，即可解得测站经纬度。

3 双星矢量天文导航定位

假设分别观测了两个天体σ1和σ2，其位置矢量分别为和，它们在地心赤道坐标系和地平坐标系中的矢量可表示为

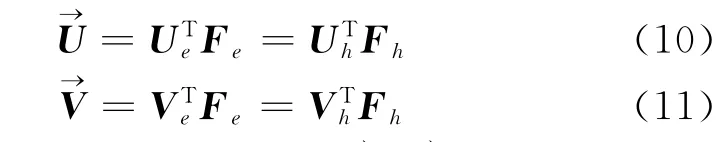
式中，Ue、Ve和Uh、Vh分别为、在地心赤道坐标系和地平坐标系中的方向余弦，根据式 （1）及式 （3）可表示为

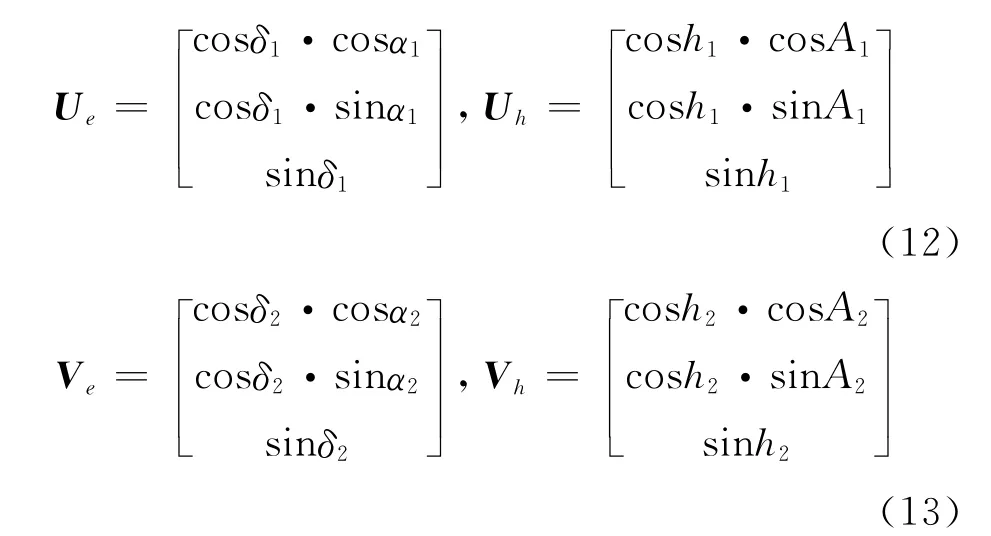
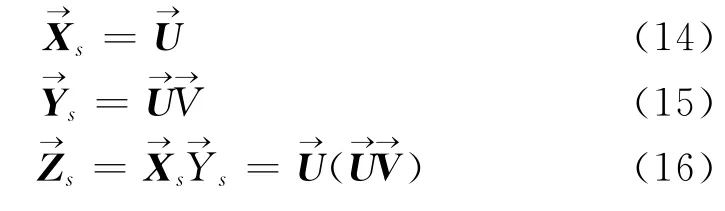
对坐标基进行单位化

记该坐标基为Fs

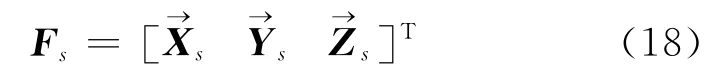
将式 （10）、式 （11）分别代入式 （14）、式（15）及式 （16）可得

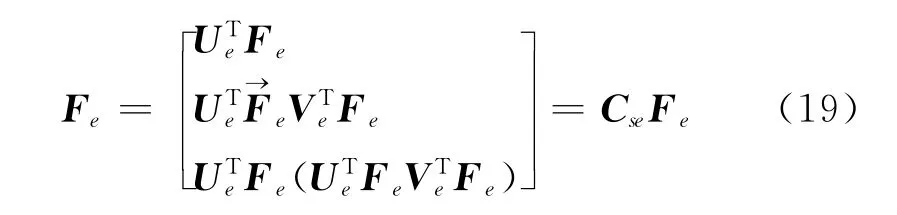
其中，Cse为坐标基Fe和Fs之间的转换矩阵，同理可得

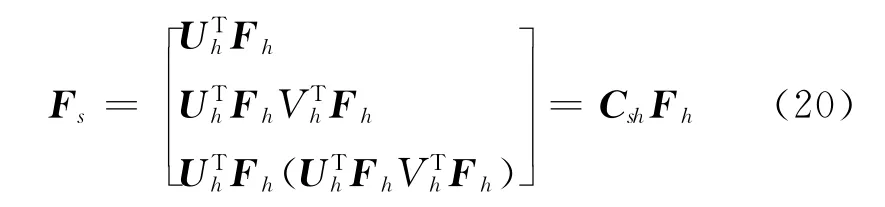
式中，Csh为坐标基Fh和Fs之间的转换矩阵，令坐标基Fh和Fe之间的转换矩阵为Ceh，由式 （19）及式 （20）可得

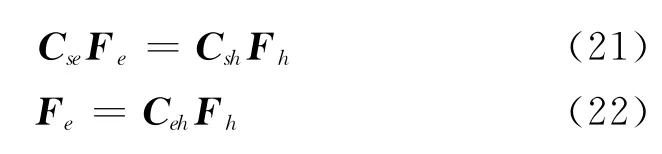
因此即可求得

根据Fh和Fe之间的转换矩阵Ceh和式 （9）即可解算测站的经纬度 （λ，φ），文献 ［10］已进行过详述。

4 多星矢量天文导航定位

4.1 方法一

若同时观测了多个天体，实现多星矢量定位的一种方法是选择其中任意两个天体按照第3节的方法解算经纬度。理论上所有解得的经纬度应该一致，但是由于观测误差的存在，导致其结果必然存在差别，可根据最小二乘法加权求解测站经纬度的最优估值，具体原理为［11］：设共观测了N个天体，则可构成个矢量对，从而求解得到测站经纬度为 （λi，φi），其中i＝1，2，…N（N－1）/2。设和之间的夹角为θi，若认为所有天体位置矢量的观测精度一致，则容易证明，当和正交，即θi＝90°时的定位误差最小，当θi＝0o或θi＝180o时定位误差最大，故设定 （λi，φi）的权为

则根据最小二乘平差原理，最终的经纬度为［8］

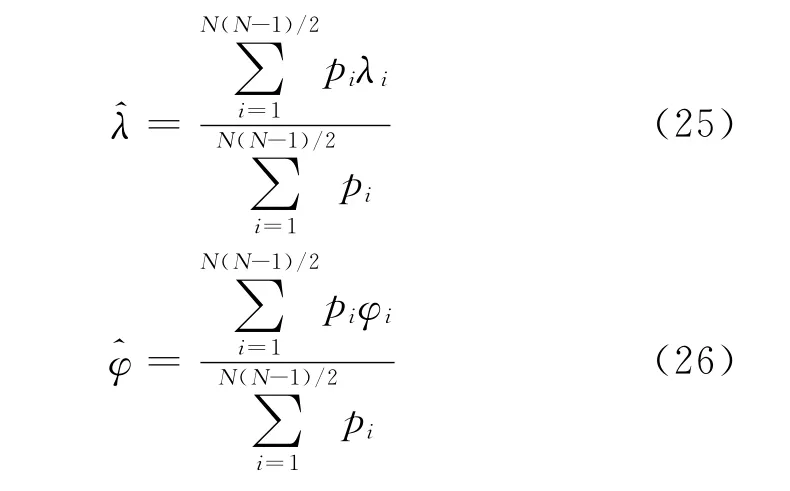
4.2 方法二

基于式 （10）建立误差方程，其原理是根据同一个天体在两个坐标系中的矢量差异最小从而求解转换矩阵，再根据转换矩阵求解测站经纬度。

同一个天体在地心赤道坐标系和地平坐标系中的位置矢量可如式 （12）表示，将地平坐标系旋转到与地心赤道坐标系相重合，设三个旋转欧拉角分别为 （εx，εy，εz），可由旋转矩阵A表示为

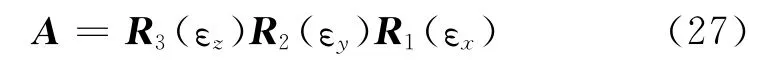
于是可得到第个i天体位置矢量在两坐标系之间的转换关系式为

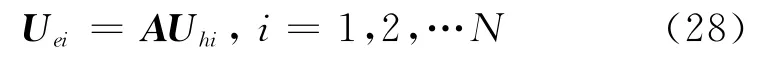
由于观测误差的存在，导致式 （28）不可能严格成立，因此可建立误差方程如下

式中，为待估矩阵，其中包含的三个旋转参数为未知参数，其估计准则可设为

式中，‖·‖表示欧式二范数，这就是著名的Wahba问题［12］，目前有多种解法可求解得到旋转参数 （εx，εy，εz）或旋转矩阵A。根据式 （9）可知

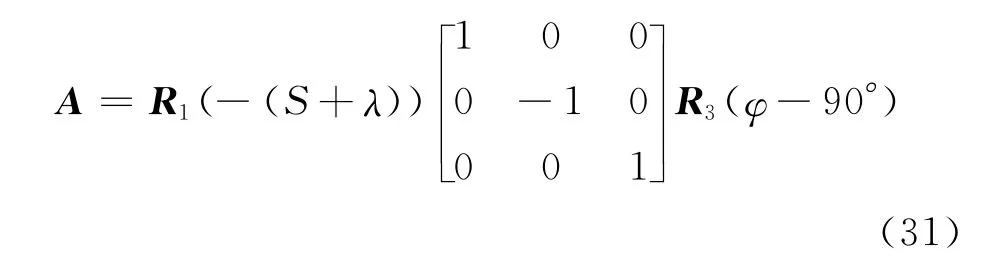
根据式 （31）即可解得测站的经纬度 （λ，φ）。

5 结束语

传统的基于球面三角形或高度差的天文定位方法只能利用天体的高度观测信息，而忽略了天体的方位观测信息。多星矢量天文导航定位方法同时考虑天体的方位角和高度角，并将每一个天体的观测位置作为一个矢量进行计算，其核心是求解地平坐标系到地心赤道坐标系之间的转换矩阵，因为其中包含测站位置信息。这不仅提高了观测量的利用率，而且能用于高精度、高自动化、大数据量的天文导航定位。需要指出的是，本文为方便推导首先假设测者载体坐标系与地平坐标系重合，而实际导航定位过程中只需要利用水平基准装置测得运载体的二维水平倾角，就能得到载体坐标系与地平坐标系之间的转换矩阵，然后即可按照本文所述方法实现多星矢量导航定位。

［1］季必达，冯惠兰.跨向21世纪的天文导航应怎样发展［C］//世纪之交的导航技术文选.西安：中国电子学会导航分会，1998：30－38.

［2］王安国.现代天文导航及其关键技术［J］.电子学报，2007，35（12）：2347－2348.

［3］王安国.导航战背景下的天文导航技术—天文导航技术的历史、现状及其发展趋势［J］.天文学进展，2001，19（2）：326－330.

［4］李临.国外天文导航技术与装备最新发展综述［J/OL］.［2012－12－26］.http：//www.cqvip.com/Main/Detail.aspx？id＝27671690.

［5］何炬.国外天文导航技术发展综述［J］.舰船科学技术.2005，27（5）：91－96.

［6］VULFOVICH B，FOGILEV V.New Ideas for Celestial Navigation in the Third Millennium［J］.The Journal of Navigation，2010，63（2）：373－378.

［7］SEIDELMANN P K，DOGGETT L E，JANICZEK P M.Algorithms，Calculators，and Computers for Celestial Navigation［J］.Proceedings of the IEEE，1983，71（10）：1201－1204.

［8］张一平，龚志辉，王勃.基于大倾角的角锥体空间后方交会研究［J］.测绘工程，2012，21（2）：17－20.

［9］郁丰，熊智，屈蔷.基于多圆交汇的天文定位与组合导航方法［J］.宇航学报，2011，32（1）：88－92.

［10］黄维彬.近代平差理论及其应用［M］.北京：解放军出版社，1992：23－27.

［11］张超，基于电子经纬仪的天文测量系统及应用研究［D］.郑州：解放军信息工程大学，2009.

［12］WAHBA A.Least Square Estimate of Spacecraft Attitude［J］，SIAM Review，1965，7（3）：409－411.