最短路算法及其在物流管理中的应用

余丽

（肇庆医学高等专科，广东肇庆526020）

最短路算法及其在物流管理中的应用

余丽

（肇庆医学高等专科，广东肇庆526020）

本文介绍了最短路的两种算法，并介绍了它们在物流管理中的若干应用.将Dijkstra算法与Floyd算法用于解决物流管理中的配送路径问题以及配送中心选址问题，并对这两种算法进行比较.

Dijkstra算法；Floyd算法；最短路

1 引言

最短路问题是交通网络分析中的一个重要的问题，它是资源分配、路线设计及分析等优化问题的基础.给定一个网络，如何求它从某点到其它点的最短路，或者如何求任意两点间的最短路?对此，已有很多好的算法.

最短路算法在物流管理中有广泛的应用.物流业被人们看作是世纪经济发展的新领域，在大力发展物流的同时,人们面临着一个共同的问题：即物流配送中心如何进行合理的选址，如何选择合适的配送路径.物流中心选址及配送路径的选择是否合理直接关系到企业各项经营成本及其获利程度.因此，合理选择物流配送中心及配送路径对于物流系统的规划至关重要.而最短路算法正可以为物流配送中心选址及配送路径选择提供强有力的理论支持.

2 最短路算法

2.1 Dijkstra算法

Dijkstra算法是一种通过源结点出发到网络当中其他的地方各个点，从中寻找最佳的路径和最短的通路的著名的算法.目前，Dijkstrs算法是大部分系统在解决最短路径的问题时所应用的理论基础，不同的系统对这种算法采用的时候实现的方式也是不同的.总的来说，该算法其主要的思想就是从源结点出发，按照路径的长度的递增次序，每一次找一个结点跟源结点之间的最短通路，然后不断继续地寻找，直至把全部的结点找到为止，因此就产生了最短路径.

Dijkstra算法的基本思想如下：

Dijkstra算法的基本思想是从图G中的n-1个独立割集中的每一个都选取一条最小的边，从而构成一个最小树.现叙述如下：设图G的点综合为（x={1,2,3,…,n}），边eij的权为wij.

第1步置u1=0，uj=w1j，j=2，3，…，n，P={1}，T={2,3,…, n}；

第2步在T中寻找一点k，使得

置P=PU{k}，T=T-{k}.若T=Ø，终止；否则，进行第3步.

第3步对T中每一点j，置uj=min{uj，uk+wkj}，然后返回第1步.

该Dijktra算法其实就是在保证局部距离的最短来更好地获得整体距离最短，是一种以局部来计算总体的贪心的策略的算法.如果从源点到其中任意点的路径不存在，那么可以假设该点的最短路径是一条长度为无穷大的虚拟路径.通过这个的分析，我们可以知道Dijkstra算法过程是由没有被确定为最短路径顶点的全部顶点中选择出一个权值最小的弧段，直至对比得到这一点顶点为止，然后仍旧不断地继续前面相同的工作，不断地反复循环.

Dijkstra算法在计算任意一个点到其他的点的最短路径的时候一共需要两次的循环，其时间的复杂度是O(n2).因此在计算一对顶点之间的最短路径的时候，需要以每一个顶点作为源点.如果执行算法n次，那么总的执行的时间的复杂度是为O(n3)，所以要选择一个弧段是权值是最小的话，就必须把全部还没确定的顶点都来扫描一次，如果数据量比较大的话，就会对计算机的速度产生较大的影响.

2.2 Floyd算法

Floyd算法又称为弗洛伊德算法，插点法，是一种动态规划的算法，用于寻找给定的加权图中顶点间最短路径的一种算法.Floyd算法在所以顶点之间的最短路径的算法中是很具有代表性的，其核心的思想是通过一个图的权值矩阵求出它的每两点间的最短路径矩阵.每次迭代求出的是只经过点集的某个子集的最短路径（一般来说初始矩阵就是邻接矩阵），这个子集在每次迭代中都加多一个点，当全部的顶点都作为中间顶点的时候，就可以求出最后的权矩阵，这时就反映出全部的顶点之间的最短的距离.

其算法思路如下：单独一条边的路径也不一定是最佳路径.从任意一条单边路径开始.所有两点之间的距离是边的权的和，(如果两点之间没有边相连,则为无穷大）.对于每一对顶点u和v，看看是否存在一个顶点w使得从u到w再到v比己知的路径更短.如果是更新它.不可思议的是，只要按排适当，就能得到结果.dmij为从节点i到节点j的最短距离.

3 最短路算法在物流管理中的应用

随着经济的全球化迅速发展和信息科技技术的突飞猛进，物流的配送技术也随着迅速提升.物流配送与我们先进的信息科技技术以及数学模型的工具也是息息相关，紧密地结合在一起，通过应用各种优化的方法对物流配送当中的各个环节进行管理，甚至进行决策，从而实现了最佳的配合.同时，最短路算法在物流配送中能够适应现代物流的特点，可以达到减少成本和提高经济效益和物流效益的效果.

3.1 最短路算法中物流配送路径的选取中的应用及算法比较

例1现有一批食品，打算由v1汽车站配送到v5大型超市，寻找一条最短的路线.经过实际测量，得到以下路线网络图，如图1所示.

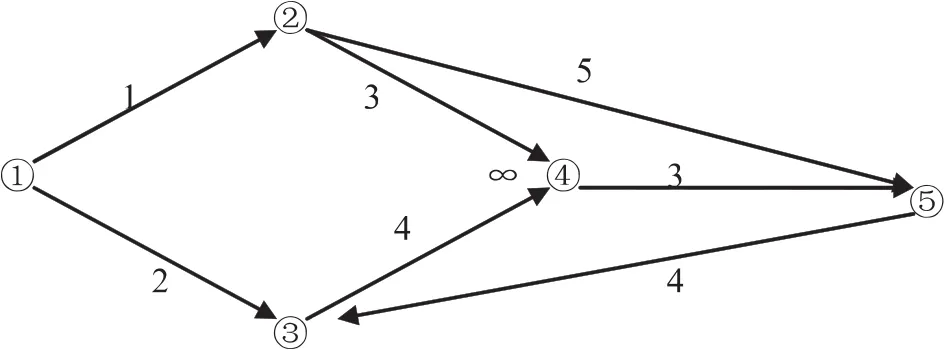
图1

3.1.1 用Dijkstra算法计算

（1）求出v1到v2的最短距离为1千米，v1到v2的最短距离为2千米，v1到v4的的最短距离为∞千米，v1到v5的最短距离为∞千米.由于v1到其他各距离最小为1，所以保留边e12.

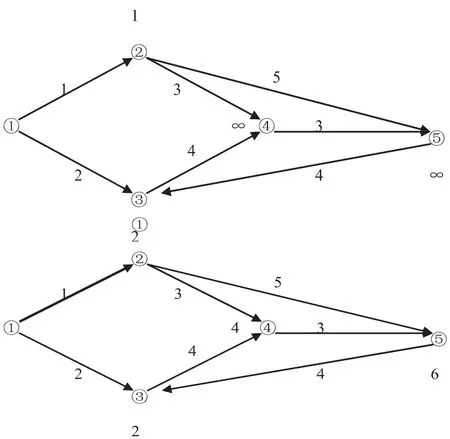
（2）仍用Dijkstra算法计算v2到v3、v4、v5的距离；取(ui,u2+w2i)，保留该点以及之前的点和边.

（3）重复进行之前一步，直到找出最短路径为止.迭代过程如下：

根据上面的步骤，可以得到从v1汽车站配送到v5大型超市的最短路径长度为6，即走v1v2v5.

3.1.2 用Floyd算法计算

Floyd算法主要用距离矩阵来求解，所以先要构造n个矩阵D0，D1，…Dn.本例中n=5，从D5矩阵中可以直接读出到相互之间的最短距离.

根据Floyd算法来解题,如下：

第一步:确定矩阵D0.如果顶i和j之间有边相连等于该边长度，如果没有.由图2可知

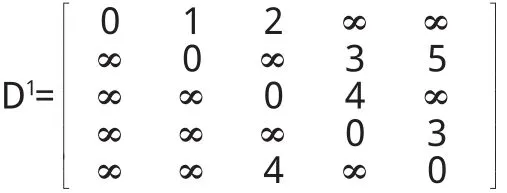
第三步：采用类似的办法可得D2,D3,D4,D(5)矩阵为:

D5的各元素值就是相应顶点间的最短路径.D5矩阵中对应的就是v1到v5相互之间的最短距离，显然可以看出两地之间的最短路径长度为6.

通过上面的例子可以了解到：Dijkstra算法通常用在计算一个点到其他的点之间的最小的路径，它在搜索的过程中，刚好与物流系统当中由一个中心点到其他点从近到远的配送方式一致：虽然Flody算法是求出每两个点间的最短的路径，可是它仅仅是求出两点间的最短路径的长度，却未能对整个路径的结点作标示，这对物流配送查询途径路径造成困难.两者相比之下，Dijkstra算法的性能较为稳定，同时也比较适合网络的拓展变化，因为选择Dijkstra算法为物流配送运输路线的基础算法.

3.2 基于最短路算法的物流中心选址方法

本文中最短路算法包含Dijkstra算法和Flody算法，也就是顶点对间的最短路的算法和全部顶点之间的最短路算法.Dijkstra算法在物流的配送运输中能够合理的进行决策和分析，而Flody算法比较适合选择合理的物流中心，从而使物流的总费用达到最少的效果，但是在选择物流中心时，由于一些约束的条件限制，导致选择物流位置只能在特定的一些区域，同时，物流运输的费用与物流运输的距离呈非线性的关系.

下面结合实例来说明最短路径说法在物流配送中心选址中的应用.

例2已知定点①、②、③、④,各点间的费用如图2所示，在四个点中选定一个点为物流的中心，使得该点到其他每个点的费用是最小的.

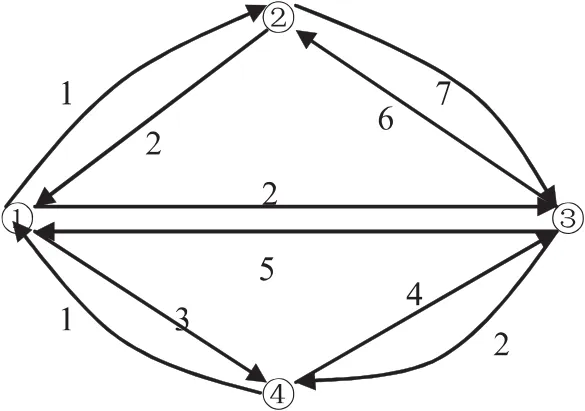
图2

3.2.1 根据Dijkstra算法来解题,如下：

反复应用Dijkstra算法，求出每一个候选地到其它各点的最短路径，由于过程较多，只给出如下结果：

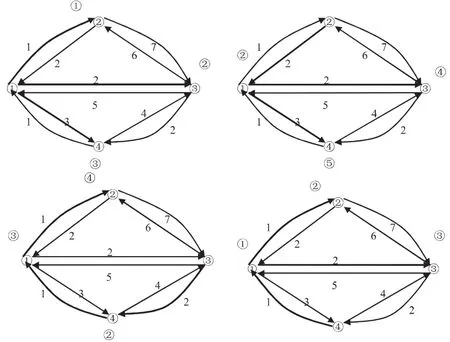
利用Dijkstra算法，得到上面的结果，通过观察可以得出①到②的最短距离为1，①到③的最短距离为2，①到④的最短距离为3，由此，①到②、③、④各点最短距离和为6同理，②到其它处最短距离和为11，③到其它处的最短距离和为9，④到其它处的最短距离和为6.比较各处到其它各处费用和的大小，可知①和④处到其它各点的费用最小.因此，①和④处就经济要素而言是最优的.

3.2.2 根据Floyd算法来解题，如下：

第一步：确定矩阵D0.如果顶i和j之间有边相连等于该边长度，如果没有，而.由图4可知

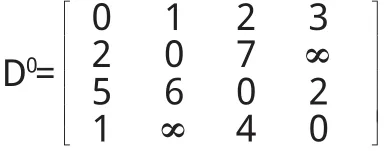
由此可知

第三步：采用类似的办法可得D2，D3，D4矩阵为

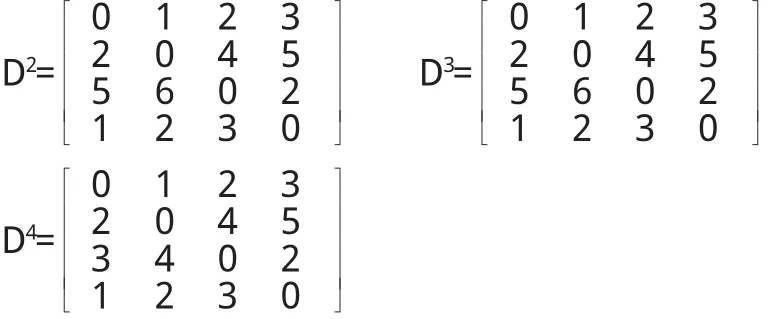
D4的各元素值就是相应顶点间的最短路径.第一行值之和即为①处到其它三处的物流费用的和，可知①到其它的费用和为6，②到其它处费用和为11，③到其它处的费用和为9，④到其它处的费用和为6.比较各处到其它各处费用和的大小，可知①和④处到其它各点的费用最小.因此，①和④处就经济要素而言是最优的.

Dijkstra算法是求最短路径最常用也是最有效的方法，但是它只能求从某一顶点到其余各顶点的最短路径.若是用于配送中心的选址问题的情况，对于这种情况，就得重复多次用Dijkstra算法，计算起来比较复杂.而1962年Floyd提出了求任意两点间最短距离的算法，就能更好的用于这种情况的解决.Dijkstra算法主要是用来标记路径，而Floyd算法则能在矩阵中直观的看出结果来.但是，当配送中心候选地较多时Floyd算法也会显得相当累赘.

4 结语

本文对最短路算法在物流配送中选用的方法进行了分析，同时，最短路算法对物流配送也起到重要的作用，不仅能够规划调整物流配送的路线，而且有效地节约物流配送成本.本文将Dijkstra算法与Floyd算法分别应用于物流管理中的配送路径问题以及配送中心选址问题，并对这两种算法进行比较.认为Dijkstra算法在物流配送路线规划方面比较适合，而配送中心选址问题用Floyd算法求解则更简洁.

〔1〕甘应爱,田丰,李维铮,等.运筹学[M].北京：清华大学出版社，2005.

〔2〕傅彦.离散数学及其应用[M].北京：高等教育出版社，2007.

〔3〕王燕,蒋笑梅.配送中心全程规划[M]北京:机械工业出版社，2004.

〔4〕刁在筠,等.运筹学(第二版)[M].北京:高等教育出版社，2005.

〔5〕耿娟.工业企业物流网络规划[M].西安:西安建筑科技大学，2007.

TP301.6

A

1673-260X（2013）11-0020-03