融合学习算法的单帧图像超分辨率复原

黄全亮，刘水清，孙金海，陈 柯

融合学习算法的单帧图像超分辨率复原

黄全亮1，刘水清1，孙金海2，陈 柯1

1.华中科技大学 电子与信息工程系，武汉 430074

2.电磁散射重点实验室，北京 100854

1 引言

图像超分辨率复原的目标是通过软件方法突破系统的成像极限，对低分辨率的降质图像进行复原处理，将它重建成趋向于理想的图像。该技术最初即是以单张影像复原的概念提出的[1]。之后多帧融合技术被引入该领域，也相继提出了多种算法。常见的超分辨率复原方法可分为频域法和空域法两种[2]，后者因为能够方便地引入先验知识成为当前研究的主流。经典空域法[2-3]又可按其原理分为集合论方法（如凸集投影法）与概率方法（如极大似然、最大后验概率法）等。

对于一些实时性较高的运用（如遥感成像、目标探测等）仍要对单帧图像进行复原处理，又由于成像原理和设备条件的限制，所得图像的降质程度很高，这对算法的要求更加苛刻，相应的空域复原方法对于观测模型的要求也更为严格。

在这一应用背景下，首先面临的是严重的病态问题，解决该问题的思想称为正则化思想。1973年，Hunt将正则化方法应用于解决图像复原的问题。文献[4]提出加权空间复原算法，文献[5-6]提出非线性正则迭代法以及正则迭代图像复原法，这些方法均通过解非线性优化问题来减少图像的边缘模糊并保护重要细节信息。选取何种正则化方法，并利用图像的局部特征，加入动态自适应处理，是问题的关键。此外，在一些运用中可以预先得到与待处理图像相关的高分辨率基准图像作为参考，相应的学习和训练算法常被引入处理流程中作为补充。早期的学习算法从图像类推技术[7]中演化而来，并很自然地引入了金字塔多分辨率模型[8]。此类方法适合处理单帧图像，但普遍存在对训练集相关性要求高，和搜索速度慢等问题。Freeman等人提出了一种基于例子的超分辨率方法[9]，一定程度上解决了上述问题，使学习算法趋于成熟，并开始常见于实际应用中。针对具体的复原问题，还需要对算法性能进行优化。综合上述分析，可整合出一个有针对性的单帧图像超分辨率复原流程。

2 算法分析

2.1 图像观测模型

考虑单帧图像，若图像的退化过程是线性移不变的，高分辨率（HR）图像和低分辨率（LR）图像之间的正向模型的矩阵形式可表示为：

其中 y为退化图像，x为待复原高分辨率图像，n为加性噪声的行排矢量。

H为图像的退化矩阵，描述图像的降质原因和退化过程，可以看作几个模糊算子和欠采样算子的相乘，其对应的系统函数h称为退化函数或降质函数。对于二维图像来说，退化函数h可以看作对图中每个像素点的扩散行为的描述，因此也被称作点扩散函数（PSF）。估计出准确的PSF是图像复原的前提。不同复原问题中的PSF是具有多样性的，但在一般情况下，它的类型却又是有限的。构成退化函数的常见模糊算子包括高斯模糊、均匀散焦模糊、运动模糊等。对于实际的成像系统，还可以采用对一系列标准测试图像进行成像实验的方法，得到其退化函数。

2.2 自适应正则化方法

从观测模型可见，图像复原作为一个逆过程是一个病态（不适定）问题。使病态反问题的求逆过程稳定而采用的方法称为正则化方法。单帧图像复原的病态问题尤为严重，因而正则化处理是必要的。

正则化方法的基本思想是利用关于解的先验知识，构造附加约束把不适定问题转化为适定问题。通常需要求解如下表达形式的目标泛函的极小值：

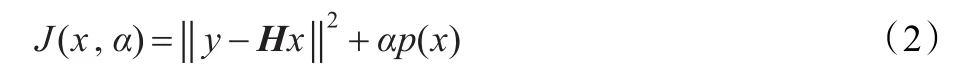
其中，d(x)=‖y-Hx‖2为数据拟合项，p(x)为附加的正则项，α为正则化参数，起平衡前二者的作用。正则项一般用来衡量信号的某种奇异性，对未知图像 x形成一个约束。通常：

其中R是约束算子，它根据图像的先验知识对解进行约束。这种思想体现出图像重建问题的本质就是在充分拟合观测数据的前提下，使某种奇异性度量最小，从而寻找理想的解x。因此如何选取约束算子正是区分不同正则化方法的标志。

当R为常数时，式（2）为简单的Tikhonov正则化。为了确保问题的连续和解唯一性，需要用到相对复杂的基于一阶微分或二阶微分的高通滤波算子。因此，本文采用阶数为2的Phillips正则化，它能更好地抑制近似解中的高频振荡噪声。其对应的泛函如式（4）。

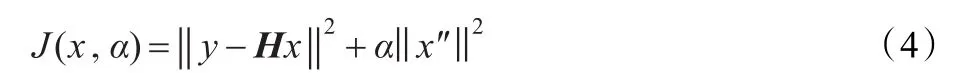
通过与二阶差分算子C（也就是Laplace算子）卷积来计算图像x的二阶差分，代替x的二阶导数，即约束算子R=C。计算过程中，采用空间域迭代下降算法求解复原图像。迭代形式和正则化参数动态更新形式分别如式（5）（6）：

为保证目标函数的凸性和收敛性，须有0＜α＜1。式（6）定义的正则化参数能最小化噪声能量，步长修正因子取经验值15。迭代终止条件如式（7），当两次迭代结果的能量差值相对于迭代结果足够小时，认为已稳定收敛，取迭代结果 f。

当正则化方法针对全局进行相同的约束处理时，称该方法为全局性方法，它的不足在于图像的复原结果不能在保持边缘和平滑噪声之间做到平衡。因此需要提出一种自适应正则化方法，根据图像的局部纹理变化对复原和平滑加以自适应性控制[10-11]，自适应算法的实现仍用到迭代计算，迭代形式（5）变为式（8）：

其中，矩阵W 的元素为图像对应局部正则化参数的权系数，称为权系数矩阵。它的取值由所对应的图像局部特性决定，并随着迭代过程按式（9）动态更新。

2.3 学习搜索算法

基于学习的超分辨率方法是相对于传统的基于重构的方法提出的，它弥补了后者过多依赖于精确模型的不足，也不似传统复原方法在理论上存在分辨率提升的上限[8，12]。这类方法通过一系列已有的高分辨率基准图像形成训练集合作为外部信息源，以某种搜索和匹配机制将其中的信息添加到待复原的图像中，从而实现分辨率的提高。最常用的信息匹配映射方式是将图像分块处理，再依照某个距离判据为每个观测图像块搜索最接近的训练图像块，最后从对应的基准图像块中提取细节作为补充。

学习算法由于有外部经验数据的支持，通过学习添加的图像细节可作为额外的补充和修复，且有时更接近真实。基准图的相关性和搜索的效率是制约这一算法的主要问题，在下文的分析中还可以看到，学习过程中类似于空域法中病态现象的出现，还需针对这些问题引入相应的优化方法。

首先是建立精简有效的训练集，尽量通过预处理减少搜索过程的复杂度，提高训练集的适用性。本文从训练图像库中产生成对的带通图像和高通图像对作为训练和学习的依据。对训练图像库中的每一帧高分辨率图像进行降质处理，降质的类型与复原处理中想要去除的相一致，然后进行降采样处理生成低分辨率图像。再对其进行三次样条插值，生成一幅具有所需像素数但缺乏高分辨率细节的图像。在训练过程中，有价值的信息为插值图像和原始高分辨率图像间的差值，即后者独有的高频信息，以及差值信息与低分辨率插值图像的对应关系，其他信息可以丢弃。然后对低分辨率图像和高频信息图像进行分块，大小分别为5×5和7×7，并按照其对应关系进行存储，至此训练集建立完成。

然后是搜索过程的优化，本文采用最先最优（best first）原则在训练集中进行最速下降搜索，以式（10）所示欧氏距离函数评判最佳匹配。

当基准图相关性不强时，在搜索过程中还会出现一种情况：对于某一给定的低分辨率输入图像块进行匹配搜索，如果从训练集合中取多个最近似的样本图像块，则其中每一个都和输入块非常相似，但它们所对应的高分辨率块却又是截然不同的。

这一现象与上文中描述的反问题的病态性十分相似，它说明仅凭局部块自身并不足以预估可能的高分辨率细节信息，由此想到考虑图像块的空间邻域关系，对搜索过程加以约束。

在图像分块时，如图1所示，使低分辨块的边缘与其邻域像素形成重叠（重叠1个像素，对应的高分辨率块重叠2个像素），在进行搜索时，预测原则如下：对每个低频输入图像块，首先在训练集中寻找与其最相似的多个低频图像块；然后，要求高频预测图像块在重叠部分与其邻域尽量保持一致，即保证高频预测块与相邻块（邻域数据）具有局部兼容性和平滑性。

图1 图像块之间的重叠关系

因此，搜索向量由两部分拼接而成：低频图像块内的像素与实时预测阶段中高频图像块邻域重叠区域内的像素。前一步预测的高频数据（作为左、上边框）用来辅助选择最佳匹配对。对训练数据库要做相同处理，与搜索向量形式相匹配。

引入参数γ控制低分辨率图像块的数据匹配和高分辨率图像块重叠部分的邻域兼容之间的平衡关系（M与N为图像块尺寸，分别取为7、5），其中系数0.25为经验取值：

总结上述内容，算法的学习过程如图2所示，因为分块之间有重叠，每得到一个输入图像块，都在之前已恢复的高频信息中提取左上边框，合成搜索向量，再与经过相同处理的训练集进行匹配，得到当前输入图像块的最优高频信息输出。

图2 学习算法中的学习过程示意图

2.4 算法整合

综合上述算法，提出如图3所示超分辨率方法流程。图中第一行描述2.1节所述的降质过程，余下部分为复原的处理过程。

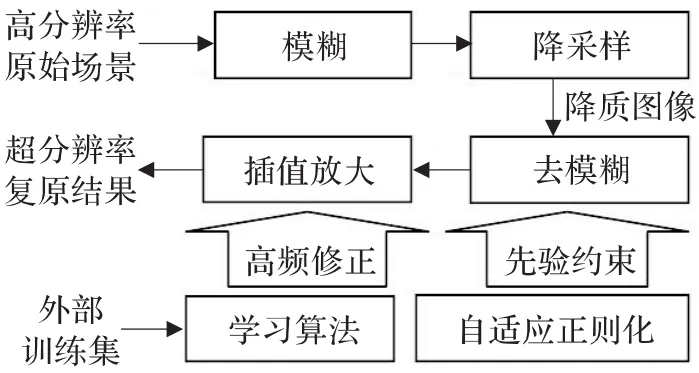
图3 降质过程及复原算法流程图

根据观测模型的线性移不变性假设，超分辨率复原处理在去模糊和升采样上的顺序可以是任意的，只是模糊算子应根据采样算子进行相应的调整。由于复原问题所需要的放大系数是确定的，而且学习算法拟合高频信息的效果也依赖于观测图像的质量，因此，对降质的低分辨率图像先采用自适应正则化方法去模糊，再利用学习算法插值放大，这样的算法流程更为合理。

自适应正则化算法与学习算法的流程如2.2节与2.3节所述。可通过仿真实验对已知原始高分辨率图像的降质图像进行重建，以检验该流程的复原效果。

3 实验结果

3.1 自适应正则化仿真

如图4所示，对一幅原始场景光学图像进行强度与半径均为3的高斯模糊，及半径为2的散焦模糊，得到降质图像，再对降质图像用正则化方法和自适应正则化方法进行复原。通过峰值信噪比（PSNR）来量化复原效果，其中N为像素点数：

图4 正则化方法仿真结果

由仿真结果可见，通过全局Phillips正则化复原的图像质量在视觉品质和PSNR上均有所提升，但是由于算法不能有效区分图像边缘和细节，复原结果中的局部细节恢复较差，且在边缘处有轻微振铃效应。考虑图像的局部特征，采用自适应正则化方法复原的图像质量明显提升，局部细节得到很好的恢复，但是复原结果中由于迭代中的卷积过程，仍然出现了一些寄生波纹失真。因此，为进一步改善超分辨率效果，在下一步插值放大步骤中引入学习算法修复更多图像细节。

3.2 学习算法仿真

按照2.3节所述，对选用的高分辨率基准图像进行滤波和分块存储处理，分别建立人脸图像训练集（包含7 889个图像块）和建筑图像训练集（包含28 046个图像块）。

首先为验证改进的学习算法的有效性，本文选用具有代表性的小波特征金字塔局部最优匹配（OLM）算法[3]作为对照，由于该算法对基准图相关性要求较高，搜索速度较慢，因此通过对算法要求较低的人脸图像超分辨率仿真进行分析，观察超分辨率算法能否合理地从训练集中选取合适的修正信息对低分辨率观测图像进行复原。

实验过程中先将一高分辨率图像模糊缩放处理作为观测图像，然后经由学习算法还原到原始分辨率。

由仿真结果可见，基于OLM算法对图像补充的信息较多，但补充信息的正确性却严重依赖于训练集与观测图像的相关性，否则复原图中修复的细节将产生过拟合现象，甚至出现类似脉冲噪声的伪像点。而改进的学习方法对图像补充的信息相对较少，但是对于基准图相关性的要求很低，同时又能通过适当的搜索方法与预测原则得到接近原图的正确修正效果，在图像模糊程度不高时，过拟合现象不明显，使得算法更为稳健。

3.3 综合实验分析

将上述两步整合到2.4所述流程中后，在降质严重的情况下，对单帧低分辨率观测图像进行复原处理，并与经典方法的处理结果对比。

如图6所示，对一帧高度降质（降采样因子0.5，高斯模糊半径为3，强度为3，均匀散焦模糊半径为3）的低分辨率建筑图像，用本文方法进行超分辨率处理，并与典型的凸集投影（POCS）算法[13]和极大似然（ML）算法（Lucy-Richardson滤波[14]）进行比较。其中PSNR根据降质前的原始高分辨率图像计算得到。从结果可见，自适应正则化方法对图像质量有较大提高，而寄生波纹和细节缺失在学习算法中得到一定的修复，同时，本文方法在单帧观测图像严重降质的情况下，与其他常用算法相比仍保持稳健有效。

4 结束语

图5 单帧人脸图像学习算法超分辨率结果

图6 单帧建筑图像超分辨率复原结果对比

在去模糊复原过程中，根据观测图像的局部特征，对Phillips正则化过程进行自适应控制，有效保障了迭代复原的效果；在插值放大过程中，利用学习算法从训练集中提取信息修复图像的高频细节，并从建立训练集和预测搜索过程等方面，使算法的基准图相关性需求和搜索效率得到了优化，学习的细节信息更为准确。实验结果表明，该超分辨率复原流程中，两个步骤的复原效果都得到了提升。正则化方法避免了高度模糊的图像在学习过程中的过拟合现象，同时，算法修复的高频信息结合了先验知识和外部参考的优势，在处理单帧高度降质的图像时依然保持了理想的复原效果。如何在算法效率和计算成本之间做到平衡，还需进一步研究。

[1]Harris J L.Diffraction resolving power[J].Journal of the Opt Soc of America，1964，54（7）：931-936.

[2]Park S C，Park M K，Kang M G.Super-resolution image reconstruction：a technical overview[J].IEEE Signal Processing Magazine，2003，20（3）：21-36.

[3]张艳.空间域超分辨率图像重建技术研究[D].郑州：解放军信息工程大学，2007.

[4]Lagendijk R L，Biemond J.Regularized iterative image restoration with ringing reduction[J].IEEE Transactions on Acoustics，Speech and Signal Processing，1988，36（12）：1874-1888.

[5]Kang M G，Katsaggelos A K.General choice of the regularization functionalin fegularized image restoration[J].IEEE Transactions on Image Processing，1995，4（5）：594-602.

[6]Kang M G，Katsaggelos A K，Ronald W S.A regularized iterative image restoration algorithm[J].IEEE Transactions on Signal Processing，1991，39（4）：914-929.

[7]古元亭，吴恩华.基于图像类推的超分辨技术[J].软件学报，2008，19（4）：851-856.

[8]Baker S，Kanade T.Limits on super-resolution and how to break them[J].Computer Vision and Patten Recognition，2000，9（2）：372-379.

[9]Freeman W T，Jones T R，Pasztor E C.Example-based superresolution[J].IEEE Computer Graphics and Applications，2002，22（2）：56-65.

[10]王艳，胡章芳.图像复原中正则化参数的自适应选择方法[J].重庆邮电大学学报：自然科学版，2007，19（6）：745-747.

[11]王晶，彭国华.空域中基于正则化的自适应超分辨率图像复原[J].计算机工程与设计，2008，29（12）：3194-3196.

[12]吴艳，陈凡胜，陈桂林.图像复原与超分辨率重构基本适用条件及提高空间分辨率上限的研究[J].红外与毫米波学报，2010，29（5）：351-356.

[13]胡飞，张瑞.一种改善被动毫米波重建图像质量的方[J].信号处理，2009，25（12）：1962-1966.

[14]孔祥龙，李玉同，远晓辉，等.Lucy-Richardson算法用于针孔图像的恢复[J].物理学报，2006，55（5）：2365-2370.

HUANG Quanliang1,LIU Shuiqing1,SUN Jinhai2,CHEN Ke1

1.Department of Electronics and Information Engineering,Huazhong University of Science and Technology,Wuhan 430074,China
2.Science and Technology on Electromagnetic Scattering Laboratory,Beijing 100854,China

In order to reconstruct a high-resolution image from single highly blurred image,a super-resolution reconstruction method combined with adaptive regularization and learning algorithm is proposed.Based on local characteristics,the dynamic adaptive control progress of reconstruction method is achieved.Train set,prediction principle and searching progress of learning algorithm is optimized to depress the relativity of example image and improve the searching efficiency.Experimental results demonstrate the availability of the method by steps,and the improvement of reconstruction result.

image reconstruction;super-resolution;regularization;learning algorithm

为从高度降质的单帧图像中重建出高分辨率图像，提出了一个结合自适应正则化与学习算法的超分辨率复原方法。该方法基于图像的局部特征，实现了正则化方法动态自适应控制过程，优化了学习算法中的训练集、预测原则和搜索过程，以降低基准图相关性要求、提高搜索效率。仿真实验分步论证了该方法的有效性，以及对复原效果的提升。

图像复原；超分辨率；正则化；学习算法

A

TP391

10.3778/j.issn.1002-8331.1208-0107

HUANG Quanliang,LIU Shuiqing,SUN Jinhai,et al.Single image super-resolution combined with learning algorithm. Computer Engineering and Applications,2013,49（23）：186-190.

国家自然科学基金（No.60705018）。

黄全亮（1973—），男，博士后，副教授，研究领域为微波遥感、图像处理、信息融合；刘水清（1987—），男，硕士研究生；孙金海（1974—），男，博士，高级工程师；陈柯（1977—），男，博士，副教授。E-mail：lsq_21@126.com

2012-08-09

2012-11-08

1002-8331（2013）23-0186-05

CNKI出版日期：2012-11-28 http://www.cnki.net/kcms/detail/11.2127.TP.20121128.1453.014.html