面向动态车辆路径的改进变邻域搜索算法

戈 军，周莲英

1.宿迁学院 计算机科学系，江苏 宿迁 223800

2.江苏大学 计算机科学与通信工程学院，江苏 镇江 212013

面向动态车辆路径的改进变邻域搜索算法

戈 军1，周莲英2

1.宿迁学院 计算机科学系，江苏 宿迁 223800

2.江苏大学 计算机科学与通信工程学院，江苏 镇江 212013

1 引言

近年来，随着生产、生活的实时通信需要，动态车辆路径问题（DVRP）已成为当前研究热点。由于DVRP是一个NP难题，且DVRP的绝大多数信息动态且不可预测，还可能出现新信息或现有信息发生变化等情况，因此，在采取分配及新请求调度决定时，必须综合考虑许多不同因素约束。变邻域搜索（VNS）作为一种有效手段可解决DVRP动态问题及路径规划优化问题。文献[1]最初提出VNS用以求解组合和全局优化问题。其中抖动和局部优化是VNS的最核心内容。

目前国内外学者主要关注于不同调度模型构建和简单高效启发式算法设计。文献[2]研究了基于混合两阶段搜索算法，第一阶段采用演化策略使车辆数最小，第二阶段利用禁忌搜索法使总距离最小。文献[3]研究了带时间窗的DVRP，并分析了次优解模型算法。文献[4]设计出求解带时间窗多车场车辆路径问题（MDVRPTW）的VNS算法，其采用两种类型邻域结构实现当前解的抖动：交换和交叉，局部搜索采用约束型3-opt算子，并利用TA（阈值接受法）思想接收部分非优解，从而避免算法陷入局部最优。文献[5]引入RVNS求解基本VRP问题。文献[6]给出了周期性VRP问题的VNS算法，采用初始解结构的节约里程法，设计出移动和交叉邻域，局部搜索策略使用3-opt算子。文献[7]利用VNS算法求解开环VRP问题。

综上，虽然国内外在DVRP问题研究上取得了一定进展，但目前DVRP的处理质量和效率还远无法满足实际需要。许多问题还需要深入研究。本文提出一种求解DVRP问题的改进型变邻域搜索算法（IVNSA），将局部搜索算子、后优化过程和模拟退火算法思想融合VNS算法框架中。并与其他算法进行比较，结果表明IVNSA可获得较为理想的求解结果。

2 DVRP问题的数学描述

变量定义如下：

带时间窗动态车辆路径问题可转化为混合整数线性规划问题。目标是最小化总成本，其目标函数为：

问题约束包括车辆约束、需求约束、路径约束和其他约束等。

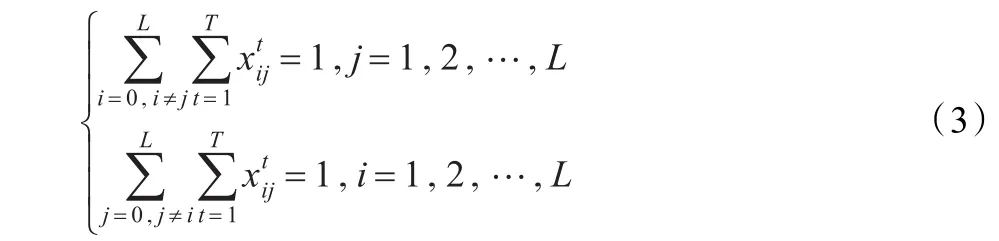
式（3）为节点到车辆的分配约束：确保各客户只有一次车辆服务，且车辆不能返回车场。

式（4）表示车辆与车场间的关系约束：确保从车场离开的车辆数不超过车辆配送中心的车辆最大数K。

式（5）为车辆与路线间的关系约束：确保同一路线上节点都由同一车辆交付。

式（6）表示节点到车辆间的分配约束：表明每一节点必须由单一车辆提供服务。

式（7）为容量约束：表明车辆交付的整体负载不应超过其容量。

式（10）表示其他约束。

3 改进变邻域搜索算法

VNS基本思想：首先在搜索过程中通过系统改变当前解的邻域结构集以拓展搜索范围，接着采用局部搜索算法求解局部最优解，然后基于此局部最优解重复上述过程，经过多次迭代后最终实现收敛目的。图1给出IVNS算法流程。

图1 IVNS算法流程图

3.1 初始解

IVNS算法利用变邻域搜索算法生成一个或多个初始可行解；分簇算法主要完成客户分配和路径规划。为了获得初始解，各客户需指派一个随机组合，利用文献[8]的节约算法构建每日车辆行驶路径。当不存在可合并两条路径时，终止算法。因此，路径数可能超过可用车辆数。这时需确定一条最少客户路径，并将该路径上的客户迁移至其他路径。需要注意的是，这可能导致无法再满足路径持续时间或容量约束，从而导致初始解不可行。因此VNS需要整合相关技术以获得可行解。可通过如下算法求得初始解，这样基本上可以满足后续需要。

3.2 抖动过程

抖动过程是变邻域搜索算法设计关键。扩展当前解搜索空间是抖动过程的主要目的，减少算法陷入局部最优解概率，从而使算法求得较好解。抖动过程的邻域结构集是VNS设计核心。而所面临的主要挑战是如何准确找出避免陷入局部最优可能性与有效性间的平衡点。抖动过程首先从当前解 x的邻域结构集中选取一个邻域结构Nk，然后根据Nk对x做出相应改变从而生成一个新解x*。

抖动过程采用两种邻域结构：插入和交换。插入是将某段连续节点从当前路径迁移至另一条路径；交换是从两条不同路径中分别选取一段连续节点，并将两者位置互换，如图2所示。各邻域的插入算子以概率 pinsert进一步加大两条路径的干扰程度；交换算子概率为1-pinsert。IVNS随机选择一种交换算子实现每次抖动路径的更改。抖动过程类似于遗传算法的交叉操作。当抖动过程结束后，只存在两条路径的交换信息；当前解的大部分特征被保留下来，这在某种程度上加快了算法的收敛速度。

3.3 局部搜索过程

为了获得VNS算法的局部最优解，局部搜索过程将对抖动过程中所生成的两条新路径分别进行局部搜索，并求出各自局部最优解。局部搜索过程是整个VNS算法框架中最耗时部分，这在很大程度上决定了VNS算法的最终解质量，因此必须充分考虑局部搜索算法设计的求解效率。本文的局部搜索算法设计主要考虑了局部搜索算子和搜索策略。为了求得短时间内质量较好的局部最优解，本文选取两种常用局部搜索算子：2-opt和3-opt，如图3所示。每次局部搜索过程只采用一种算子，并通过随机方式选择算子，2-opt的选择概率为 p2-opt；而3-opt的选择概率为1-p2-opt。采用这种混合算子可充分发挥两种算子特点，从而扩大算法解空间。

图2 插入和交换算子示意图

图3 2-opt和3-opt策略

搜索策略主要包括首次改进和最佳改进。前者是指求解过程中依次访问当前解x的邻域解，若当前所访问的邻域解xn优于x，则x=xn并更新其邻域解。重复上述步骤直到访问完x的所有邻域解。最后，将求得的x作为局部最优解。后者是指求解过程中遍历当前解x的所有邻域解，并从中选择最优邻域解xn作为局部最优解。两者相比，前者求解质量优于后者，而后者耗时更短。本文采用最佳改进策略，从而较好地平衡了求解质量和运行时间。

3.4 后期优化过程

为了加快收敛速度和提高解质量，本文提出一种IVNS算法后优化过程。完成局部搜索后，如果所求得局部最优解 xl优于全局最优解 xb，即则继续执行后优化过程以求得全局最优解[9]。后优化过程算法[10]适合求解带时间窗旅行商问题和车辆路径问题。其算法流程为：

步骤1假设待优化路径为r，长度为n，评价函数值为c。最终优化路径为r*，评价函数值为c*，并令r*=r，c*=c，k=1。

步骤2分别对优化路径r中的第k个客户节点执行解串和成串操作，从而得到优化路径r′和评价函数值c′。

步骤3若c′＜c*，则r*=r′，c*=c′，c=c′，然后跳转至步骤2；否则k=k+1，算法停止。

3.5 解接受准则

解接受准则用于判定应该接受哪一个解进入下一次迭代。若x*优于当前解x，则x*替代x进入下一次迭代；反之，利用模拟退火算法[11]的解接受准则选择进入下一次迭代解。为了避免VNS过早陷入局部最优，模拟退火算法的接受准则能够以式（11）的概率接受一定条件下的较劣解，这主要取决于VNS实际解成本差异及温度T。每迭代nT次温度T以数量进行更新，其中q0为[0，1]中的一个随机数，δmax为VNS算法的总迭代次数，初始温度值T0=10：

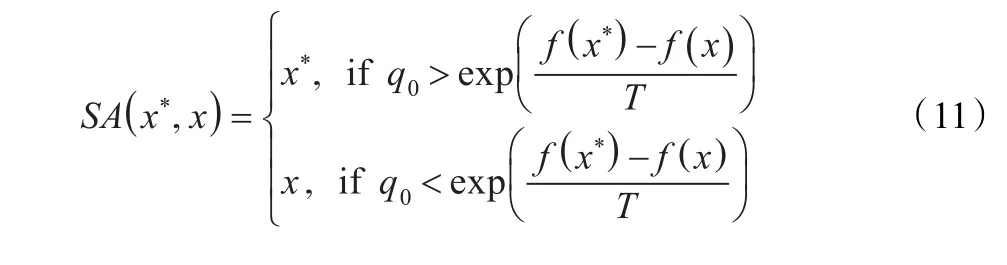
4 实验仿真及测试比较

为了评估IVNS的DVRP性能，分析算法的解质量和效率，本文从三个不同测试角度对DVRP进行实验仿真，并与其他相关算法进行比较。

4.1 四种算法的测试比较

为了比较不同算法的测试性能，此时采用文献[12]的数据集来评估IVNS的DVRP性能。

IVNS算法的各种参数初始值设置如下：

（1）模拟退火算法的参数设置：初始温度T0=10，每迭代生成温度的变化值

（2）抖动过程参数值设置：pinsert=0.2，pcross=0.15，和picross=0.1。

表1给出IVNS、遗传算法（GA）、禁忌搜索（TS）、两阶段算法（TPA）的比较测试结果。

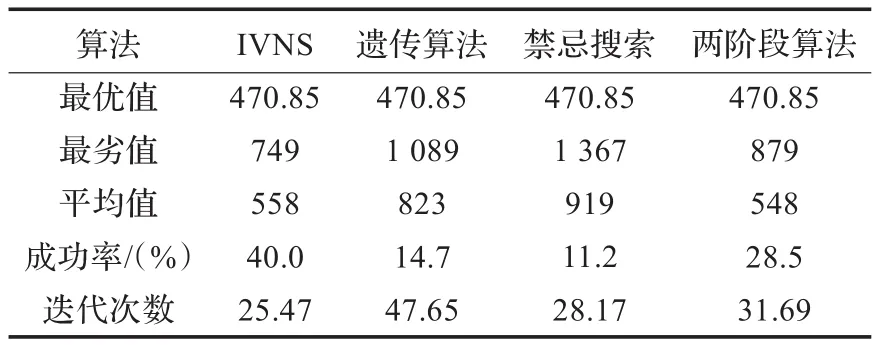
表1 不同算法的测试结果

从表1中可以看出，四种算法都可找出最优解，但最劣值和平均值存在明显差异，搜索成功率和迭代次数也存在差异。四种算法搜索成功率从小到大依次为禁忌搜索算法、两阶段算法、遗传算法和IVNS；最劣值、平均值从小到大依次为IVNS、两阶段算法、遗传算法和禁忌搜索算法；这说明IVNS的全局搜索能力最强。四种算法的迭代次数从小到大顺序依次为IVNS、禁忌搜索算法、两阶段算法和遗传算法，这说明IVNS的收敛速度最快，因此某种程度上IVNS更合适求解动态车辆路径问题。

4.2 VRPTW测试范例比较

测试用例采用Solomon编制的100节点VRPTW问题的计算范例。各范例包含100个节点，分布于100×100欧氏平面。范例分为6类：R1、R2、C1、C2、RC1和RC2。DVRPTW采用Lackner动态测试数据集。Solomon范例的每个问题，测试数据分别用五种动态度（90%，70%，50%，30%和10%）进行描述。从IVNS和Lackner算法的测试结果可得出如下结论：（1）总行驶距离除了RC1，R1和C2外，IVNS的求解都优于Lackner；（2）IVNS平均计算时间少于Lackner，且不超过90 s，这完全满足实时调度需求。从而说明IVNS搜索能力更强。

4.3 扩展测试比较

为了评估变邻域搜索算法求解大规模动态车辆路径问题的有效性，本文将文献[2]测试实例扩展至1 000个客户。测试结果如表2所示。

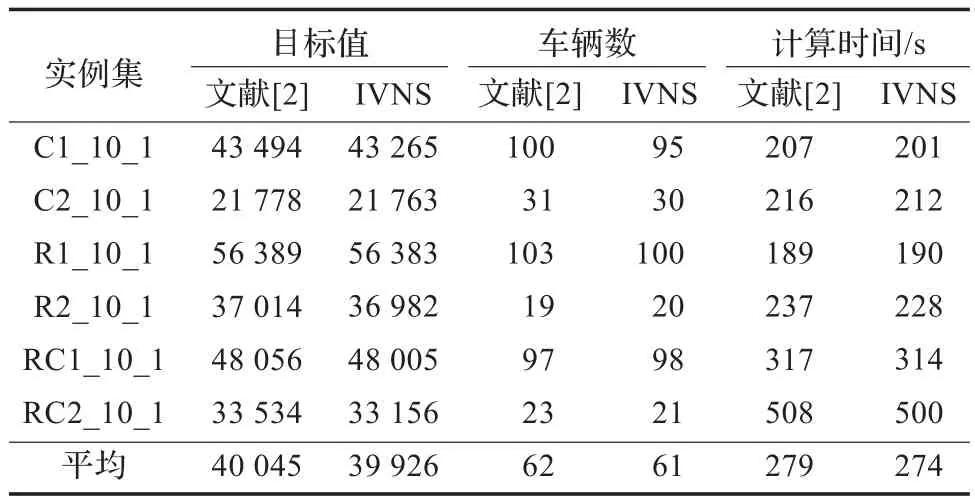
表2 文献[2]和IVNS算法的测试结果

从表2中可以看出，IVNS的平均运行时间少于Gehring，车辆数从62降至61，目标值从40 045减小至39 926。因此IVNS算法在某种程度上可求解大规模动态VRP。

5 结论

针对动态车辆路径问题，本文提出一种改进变邻域搜索算法。初始解利用节约算法求解每日车辆路径问题的路线构建。抖动过程采用插入和交换这两种邻域结构。选取2-opt和3-opt作为局部搜索算子从而获得短时间内的较好局部最优解，给出IVNS算法的后优化过程以加快收敛速度和提高解质量，采用三种不同测试用例验证改进变邻域搜索算法性能，并与其他算法进行了比较。比较结果表明，IVNS模型和算法可有效求解短时间内的DVRP问题。

[1]Hansen P，Mladenović N，Perez-Britos D.Variable neighborhood decomposition search[J].Journal of Heuristics，2001，7（4）：335-350.

[2]Gehring H，Homberger J.Parallelization of a two-phased metaheuristic for routing problems with time windows[J]. Asia-Paeific Journal of Operational Research，2001，18（1）：35-47.

[3]Müller J.Approximative solutions to the bicriterion vehicle routing problem with time windows[J].European Journal of Operational Research，2010，202（1）：223-231.

[4]Polacek M，Hartl R F，Doerner K，et al.A variable neighborhood search for the multi depot vehicle routing problem with time windows[J].Journal of Heuristics，2004，10（6）：613-627.

[5]Goel A，Gruhn V.A general vehicle routing problem[J].European Journal of Operational Research，2008，191（3）：650-660.

[6]Hemmelmayr V C，Doerner K F，Hartl R F.A variable neighborhood search heuristic for periodic routing problems[J]. European Journal of Operational Research，2009，195（3）：791-802.

[7]Fleszar K，Osman I H，Hindi K S.A variable neighbourhood search algorithm for the open vehicle routing problem[J]. European Journal of Operational Research，2009，195（3）：803-809.

[8]Clarke G，Wright J W.Scheduling of vehicles from a central depot to a number of delivery points[J].Operations Research，1964，12（4）：568-581.

[9]王征，张俊，王旭坪.多车场带时间窗车辆路径问题的变邻域搜索算法[J].中国管理科学，2011，19（2）：99-108.

[10]Gendreau M，Hertz A，Laporte G，et al.A generalized insertion heuristic forthe traveling salesman problem with time windows[J].Operations Research，1998，46（3）：330-335.

[11]王凌.智能优化算法及其应用[M].北京：清华大学出版社，2004.

[12]王旭，葛显龙，代应.基于两阶段求解算法的动态车辆调度问题研究[J].控制与决策，2012，27（2）：175-181.

GE Jun1,ZHOU Lianying2

1.Department of Computer Science,Suqian College,Suqian,Jiangsu 223800,China
2.College of Computer Science and Communication Engineering,Jiangsu University,Zhenjiang,Jiangsu 212013,China

In order to effectively solve the dynamic vehicle routing problem with time windows,an improved variable neighborhood search algorithm is proposed and the corresponding mathematical model is established.The algorithm uses the clustering method to complete customer allocation and route planning for the construction of initial solution.Hybrid operators of insert-exchange are used to achieve the shaking process,the later optimization process is presented to improve the solution space,and the best improvement strategy is adopted,which achieves the algorithm a better balance in the solution quality and run-time.The idea of simulated annealing is introduced to control the acceptance of new solutions and the distribution of geographical location,etc, and the route selection is analyzed.Through comparison of experimental results with other algorithms it shows that the algorithm is feasible and efficient.

improved variable neighborhood search;shaking;simulated annealing;later optimization process;metaheuristic

为了切实求解带时间窗的车辆动态路径问题，提出一种改进变邻域搜索算法，并建立了相应数学模型。算法运用聚类方法完成客户分配和路线规划的初始解构建。插入-交换混合算子实现抖动过程，提出后优化过程改进解空间，并采用最佳改进策略实现算法在求解质量和运行时间上的最佳平衡，引入模拟退火思想控制新解接受、地理位置分布等，并对路径选择进行了分析。通过与其他算法的实验结果比较表明该算法的可行性和高效性。

改进变邻域搜索；抖动；模拟退火；后优化；元启发式

A

TP393；TP391.9

10.3778/j.issn.1002-8331.1308-0220

GE Jun,ZHOU Lianying.Improved variable neighborhood search algorithm for dynamic vehicle routing.Computer Engineering and Applications,2013,49（23）：71-74.

江苏省宿迁市科技创新专项基金资助项目（No.Z201211）。

戈军（1977—），男，副教授，研究方向为计算机网络安全、无线传感器网络、车辆管理等；周莲英（1964—），女，博士，教授。E-mail：gjun@sqc.edu.cn

2013-08-16

2013-10-08

1002-8331（2013）23-0071-04